2019九年级数学上册 专题突破讲练 圆的周长和弧长试题 （新版）青岛版

2019九年级数学上册 专题突破讲练 圆的周长和弧长试题 （新版）青岛版

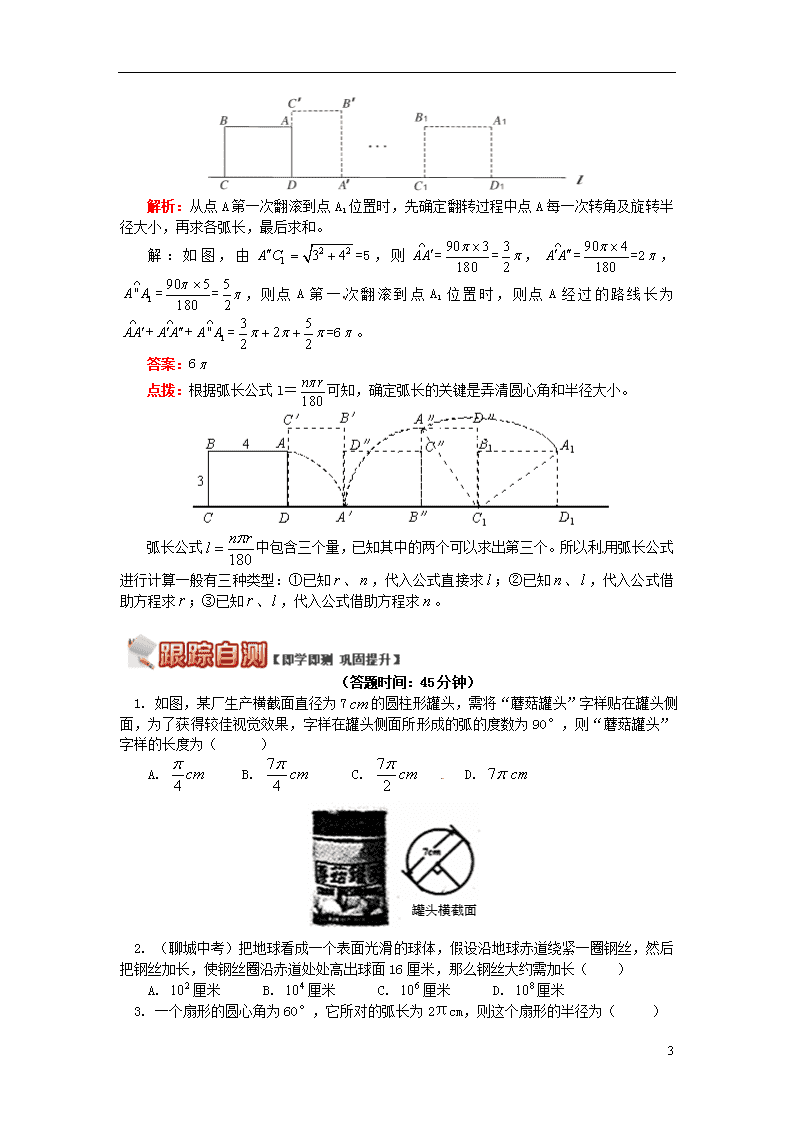
圆的周长和弧长 ‎1. 弧长公式：‎ 圆周长C=2R（其中R为圆的半径），即为圆心角是360°的弧长。因此圆心角是1°的弧长等于圆周长的，即，所以n°的圆心角所对的弧长为。即在半径为R的圆中，n°的圆心角所对的弧长的计算公式为：l=。‎ 说明：（1）在应用公式进行计算时，要注意公式中n的意义：n表示1°的圆心角的倍数。公式中的n、180都不带单位。（2）同圆中圆心角n°越大，弧长越长；相等的圆心角半径越大，所对的弧长越大，L与n、R两个因素有关。‎ ‎2. 易错点：扇形的弧长和扇形的周长不一样，扇形的周长是扇形的弧长与两个半径的和。‎ 直接利用公式求弧长 例题1 如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠ABC=120°，OC=3，则的长为（　　）‎ A. 　　 B. ‎2‎　　 C. 3　　 D. 5‎ 解析：连接OB，由于AB是切线，那么∠ABO=90°，而∠ABC=120°，易求∠OBC，而OB=OC，那么∠OBC=∠OCB，进而求出∠BOC的度数，在利用弧长公式即可求出的长。‎ 解：连接OB。‎ ‎∵AB与⊙O相切于点B，∴∠ABO=90°。∵∠ABC=120°，∴∠OBC=30°。‎ ‎∵OB=OC，∴∠OCB=30°。∴∠BOC=120°。∴的长为，故选B。‎ 答案：B 点拨：利用弧长公式计算弧长时，关键是根据题意得出圆心角、半径，而本题解题的关键是连接OB，构造直角三角形。‎ 例题2 如图，在边长为1的正方形组成的网格中，△ABC的顶点都在格点上，将△ABC绕点C顺时针旋转60°，则顶点A所经过的路径长为（ ）‎ 7‎ A. 10π B. C. π D. π 解析：由题意得点A所经过的路径是以C为圆心，CA长为半径，圆心角为60°的弧，而要求的顶点A所经过的路径长就是求以C为圆心，CA长为半径，圆心角为60°的弧长，利用弧长公式计算可得。‎ 解：∵在Rt△ACD中，AD=3，DC=1，∴根据勾股定理得：AC= ，‎ ‎∵△ABC绕点C顺时针旋转60°，‎ ‎∴顶点A所经过的路径长为 l==π。故选C。‎ 答案：C 点拨：求动点所经过的路径长，必须先分析清楚动点所经过的路径是什么。此题中的动点绕一定点在旋转，故动点所经过的路径是以定点为圆心，动点到定点的长度为半径的一条弧，从而把求长度问题转化为求弧长问题，直接利用弧长公式计算。‎ 弧长公式的逆用 例题3 一条弧所对的圆心角为135°、弧长等于半径为‎5cm的圆的周长的3倍，则这条弧的半径为 cm。‎ 解析：已知圆半径可由圆周长公式得圆周长。弧长的计算为公式：，已知圆心角为135°，故弧长为，由题意列方程可解得弧所在圆的半径。‎ 解：设弧所在圆的半径为rcm，由题意得：，解得r=40，‎ 故这条弧的半径为‎40cm。‎ 答案：40‎ 点拨：注意区别圆周长的计算公式：（）与弧长的计算公式：‎ 弧长公式在滚动问题中的应用 在旋转变换中，有时就隐含着弧长的计算，准确理解弧长公式各个量的含义，是解题的关键。‎ 满分训练 如图，矩形ABCD中，AB=4，BC=3，边CD在直线l上，将矩形ABCD沿直线l做无滑动翻滚，当点A第一次翻滚到点A1位置时，则点A经过的路线长为 。‎ 7‎ 解析：从点A第一次翻滚到点A1位置时，先确定翻转过程中点A每一次转角及旋转半径大小，再求各弧长，最后求和。‎ 解：如图，由=5，则==，==2， ==，则点A第一次翻滚到点A1位置时，则点A经过的路线长为++==6。‎ 答案：6‎ 点拨：根据弧长公式l＝可知，确定弧长的关键是弄清圆心角和半径大小。‎ 弧长公式中包含三个量，已知其中的两个可以求出第三个。所以利用弧长公式进行计算一般有三种类型：①已知、，代入公式直接求；②已知、，代入公式借助方程求；③已知、，代入公式借助方程求。‎ ‎（答题时间：45分钟）‎ ‎1. 如图，某厂生产横截面直径为7的圆柱形罐头，需将“蘑菇罐头”字样贴在罐头侧面，为了获得较佳视觉效果，字样在罐头侧面所形成的弧的度数为90°，则“蘑菇罐头”字样的长度为（ ）‎ A. B. C. D. ‎ ‎2. （聊城中考）把地球看成一个表面光滑的球体，假设沿地球赤道绕紧一圈钢丝，然后把钢丝加长，使钢丝圈沿赤道处处高出球面16厘米，那么钢丝大约需加长（ ）‎ A. 厘米 B. 厘米 C. 厘米 D. 厘米 ‎3. 一个扇形的圆心角为60°，它所对的弧长为2πcm，则这个扇形的半径为（ ）‎ 7‎ A. ‎6cm B. ‎12cm C. ‎2cm D. cm ‎4. 已知一个扇形的半径为60厘米，圆心角为150°。用它围成一个圆锥的侧面，那么圆锥的底面半径为厘米。‎ ‎*5. 如图，⊙O的半径为‎6cm，直线AB是⊙O的切线，切点为点B，弦BC∥AO，若∠A＝30°，则劣弧的长为 cm。‎ ‎6. （四川中考）点A、B、C是半径为‎15cm的圆上三点，∠BAC=36°，则弧BC的长为 ‎______cm。‎ ‎*7. 点O在直线AB上，点A1、A2、A3…在射线OA上，点B1、B2、B3…在射线OB上，图中的每一个实线段和虚线段的长均为1个单位长度。一个动点M从O点出发，按如图所示的箭头方向沿实线段和以O为圆心的半圆匀速运动，速度为每秒1个单位长度。按此规律，则动点M到达A101点处所需时间为 　 。‎ ‎**8. 如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿着过点B的直线折叠，点O恰好落在上的点D处，折痕交OA于点C，则的长为 。‎ ‎**9. 如图，已知CB是⊙O的弦，CD是⊙O的直径，点A为CD延长线上一点，BC=AB，∠CAB=30°。（1）求证：AB是⊙O的切线；（2）若⊙O的半径为2，求的长。‎ ‎**10. 如图所示，AC⊥AB，AB=，AC=2，点D是以AB为直径的半圆O上一动点，DE⊥CD交直线AB于点E，设∠DAB=，（0°＜＜90°）。‎ ‎（1）当=18°时，求的长。（2）当=30°时，求线段BE的长。‎ ‎（3）若要使点E在线段BA的延长线上，则的取值范围是 （直接写出答案）。‎ 7‎ ‎ *11. 如图，实线部分是半径为‎15m的两条等弧组成的游泳池，若每条弧所在的圆都经过另一个圆的圆心，求游泳池的周长。‎ 7‎ ‎ ‎ ‎1. B 解析：∵字样在罐头侧面所形成的弧的度数为90°，∴此弧所对的圆心角为90°，由题意可得，=cm，则“蘑菇罐头”字样的长= 。故选B。‎ ‎2. A 解析：先设地球的半径为r，则赤道的长近似为2πr cm，当钢丝圈沿赤道处处高出球面‎16厘米时，钢丝的长度近似为2π（r+16）cm，则钢丝大约需加长2π（r+16）﹣2πr =32π≈‎100 cm，故选A。‎ ‎3. A 解析：根据弧长公式，πr=2π，解得r=6，故选A。‎ ‎4. 25 解析：设圆锥的底面半径为r，则圆锥的母线长R=‎60cm，因为圆锥的底面周长等于其侧面展开图的弧长，所以2πr=，解得r=‎25cm。‎ ‎5. 解析：∵AB是⊙O的切线，∴AB⊥BO。 ∵∠A=30°，∴∠AOB=60°。∵BC∥AO，∴∠OBC=∠AOB=60°。在等腰△OBC中，∠BOC=180°﹣2∠OBC=180°﹣2×60°=60°。∴弧BC的长为cm。 ‎ ‎6. 6π 解析：如图，在⊙O中，∠BAC=36°，∴∠BOC=72°，∴根据弧长公式计算弧BC的长为：=6π。‎ ‎7. （5050 π＋101）s 解析：动点M到达A1的时间为1s，到达A2的时间为[]s，到达A3的时间为[]s，到达A4的时间为[]s，……，所以到达A101的时间为[]s=(5050 π＋101)s。‎ ‎ 8. 5π 解析：如图，连接OD。由折叠可得OB=DB=OD，∴△ODB是等边三角形，从而DOB=60°。‎ ‎∴∠AOD=∠AOB－∠DOB=50°，因此的长为=5π。‎ ‎9. 解析：（1）∵BC=AB，∴∠C=∠A=30°，∴∠BOA=2∠C=60°，‎ ‎∴∠OBA=180°－∠A－∠BOA=180°－30°－60°=90°，∴AB是⊙O的切线。‎ ‎⑵的长=。‎ ‎10. 解析：（1）连接OD，∵=18°，∴∠BOD=36°，又∵AB=，∴OB=，∴‎ 7‎ 的长==。‎ ‎（2）∵AB是半圆O的直径，∴∠ADB=90°，又∵=30°，∴∠B=60°，又∵AC为半圆O的切线，∴∠CAD=60°，∴∠CAD=∠B，又∵DE⊥CD，∴∠ADC+∠ADE=90°，又∵∠ADE+∠BDE=90°，∴∠BDE=∠ADC，∴△BDE∽△ADC，∴，即，∴BE=。‎ ‎（3）60°＜＜90°。 ‎ ‎11. 解析：如图，连接O1O2，O‎1A，O1B，O‎2A，O2B，‎ 因为⊙O1和⊙O2是等圆，∴△O1O‎2A，△O1O2B都是等边三角形，∴∠AO1B=∠AO2B=120°，‎ ‎∴周长为：2××2π×15=40π，所以游泳池的周长为40πm。‎ 7‎