鄂尔多斯专版2020中考数学复习方案第五单元四边形第23课时多边形与平行四边形课件

鄂尔多斯专版2020中考数学复习方案第五单元四边形第23课时多边形与平行四边形课件

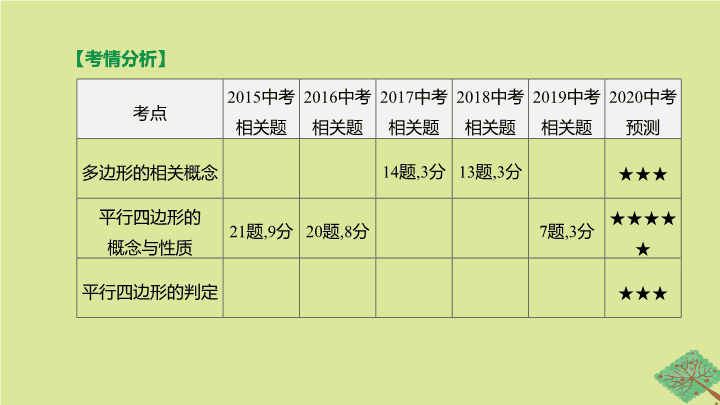
第 23 课时 多边形与平行四边形 第五单元　四边形 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 多边形的相关概念 14 题 ,3 分 13 题 ,3 分 ★★★ 平行四边形的 概念与性质 21 题 ,9 分 20 题 ,8 分 7 题 ,3 分 ★★★★★ 平行四边形的判定 ★★★ 考点一　多边形 考点聚焦 图形 性质 多 边 形 内角和 n 边形的内角和为 ① 　 　　   外角和 任意多边形的外角和为 360° 对角线 (1) n 边形共有 ② 　　　　 条对角线 ;  (2) 从一个顶点出发的对角线把 n 边形分成 ③ 　　　 个三角形   不稳定性 n 边形 ( n> 3) 具有不稳定性 ( n- 2)·180° n- 2 ( 续表 ) 图形 性质 正 多 边 形 边 各条边 ④ 　　　   内角 各个内角 ⑤ 　 　 , 且正 n 边形的每个内角为 ⑥ 　　　　   外角 各个外角相等 , 且正 n 边形的每个外角为 ⑦ 　　　   对称性 (1) 正多边形都是 ⑧ 　　　　 对称图形 , 其中边数为偶数的正多边形也是中心对称图形 ;  (2) 正 n 边形有 ⑨ 　　　 条对称轴   相等 相等 轴 n 考点二　平行四边形 定义 　 两组对边分别平行的四边形是平行四边形 性质 (1) 平行四边形的对边 ⑩ 　 　　 ;  (2) 平行四边形的对角 ⑪ 　　　 , 邻角 ⑫ 　　　 ;  (3) 平行四边形的对角线互相 ⑬ 　　 　 ;  (4) 平行四边形是 ⑭ 　　 　 对称图形     判定 (1) 两组对边分别平行的四边形是平行四边形 ; (2) 两组对边分别 ⑮ 　　 　 的四边形是平行四边形 ;  (3) 一组对边 ⑯ 　　　 的四边形是平行四边形 ;  (4) 两组对角分别 ⑰ 　　 　 的四边形是平行四边形 ;  (5) 对角线互相 ⑱ 　　 　 的四边形是平行四边形     平行且相等 相等 互补 平分 中心 　 相等 平行且相等 相等 平分 ( 续表 ) 面积 　 S = ah ( a 表示一条边长 , h 表示此边上的高 ) 相关 结论 (1) 平行四边形的两条对角线将平行四边形分成 ⑲ 　 　　 的四个三角形 ;  (2) 同底等高的平行四边形的面积相等 ; (3) 若一条直线过平行四边形的对角线的交点 , 则这条直线等分平行四边形的面积 面积相等 题组一　必会题 对点演练 1 . 一个多边形的内角和是 900°, 这个多边形的边数是 ( 　　 ) A . 4 B . 5 C . 6 D . 7 D [ 答案 ] D 　 [ 解析 ] 因为平行四边形的对角线互相平分 , OE ⊥ BD , 所以 OE 垂直平分 BD , 所以 BE = DE , 从而 △ ABE 的周长等于 AB + AD , 即▱ ABCD 的周长的一半 , 所以 △ ABE 的周长为 14, 故选 D . 2 . [2019· 遂宁 ] 如图 23-1, ▱ ABCD 中 , 对角线 AC , BD 相交于点 O , OE ⊥ BD 交 AD 于点 E , 连接 BE. 若▱ ABCD 的周长为 28, 则 △ ABE 的周长为 ( 　　 ) A . 28 B . 24 C . 21 D . 14 图 23-1 3 . [2019· 达州 ] 如图 23-2, ▱ ABCD 的对角线 AC , BD 相交于点 O , 点 E 是 AB 的中点 , △ BEO 的周长是 8, 则 △ BCD 的周长为 　　　　 .  图 23-2 [ 答案 ] 16 　 [ 答案 ] 72 　 [ 解析 ] 如图 , 过点 B 作 BF ∥ l 1 . ∵五边形 ABCDE 是正五边形 , ∴∠ ABC =108° . ∵ BF ∥ l 1 , l 1 ∥ l 2 , ∴ BF ∥ l 2 , ∴∠ CBF =180°- ∠ 1, ∠ ABF = ∠ 2, ∴ 180°- ∠ 1+ ∠ 2= ∠ ABC =108°, ∴∠ 1- ∠ 2=72° . 4 . [2018· 南京 ] 如图 23-3, 五边形 ABCDE 是正五边形 , 若 l 1 ∥ l 2 , 则∠ 1- ∠ 2= 　　　　 ° .  图 23-3 【 失分点 】 对于平行四边形的性质与判定不能准确理解 ; 构图时忽视多种情况的存在 , 考虑不全面 . 题组二　易错题 5 . 下列说法错误的是 ( 　　 ) A . 对角线互相平分的四边形是平行四边形 B . 两组对边分别相等的四边形是平行四边形 C . 一组对边平行且相等的四边形是平行四边形 D . 一组对边相等 , 另一组对边平行的四边形是平行四边形 D 6 . 在▱ ABCD 中 , AE 平分∠ BAD 交 BC 于点 E , 将 BC 分成 4 cm 和 6 cm 两部分 , 则▱ ABCD 的周长为 ( 　　 ) A . 28 cm B . 32 cm C . 28 cm 或 32 cm D . 无法确定 [ 答案 ] C 　 [ 解析 ] ∵ AE 平分∠ BAD , ∴∠ BAE = ∠ DAE. ∵▱ ABCD 的边 AD ∥ BC , ∴∠ DAE = ∠ AEB , ∴∠ BAE = ∠ AEB , ∴ AB = BE. ①当 BE =4 cm 时 , AB =4 cm, BC =4+6=10(cm), ∴▱ ABCD 的周长为 2( AB + BC )=2×(4+10)=28(cm), ②当 BE =6 cm 时 , AB =6 cm, BC =6+4=10(cm), ∴▱ ABCD 的周长为 2( AB + BC )=2×(6+10)=32(cm) . 综上所述 , ▱ ABCD 的周长为 28 cm 或 32 cm . 故选 C . [ 答案 ] 540° 或 360° 或 180° 　 [ 解析 ] n 边形的内角和是 ( n -2)×180° . 若所得多边形的边数增加 1, 则其内角和是 (4+1-2)×180°=540°; 若所得多边形的边数不变 , 则其内角和是 (4-2)×180°=360°; 若所得多边形的边数减少 1, 则其内角和是 (4-1-2)×180°=180°, 所以新多边形的内角和是 540° 或 360° 或 180° . 7 . [2018· 聊城 ] 如果一个正方形被截掉一个角后 , 得到一个多边形 , 那么这个多边形的内角和是 　　　　 .  考向一　多边形的相关概念及计算 例 1 [2018· 原创 ] (1) 七边形的内角和等于 　　　 ;  (2) 正八边形的每一个内角都等于 　　　　 , 每一个外角都等于 　　　　 ;  (3) 如果一个多边形的内角和等于 1260°, 那么这个多边形的边数是 　　　　 ;  (4) 如果一个多边形的每个外角都是 60°, 那么这个多边形的边数是 　　　　 ;  (5) 如果一个多边形的内角和等于外角和 , 那么这个多边形的边数是 　　　　 .  900° 135° 45° 9 6 4 【 方法点析 】 ( 1) 多边形的内角中最多只有三个锐角 ; (2) 多边形的边数每增加一条 , 内角和的度数增加 180 °; (3) 多边形的外角和与边数 n 无关 . | 考向精练 | 1 . 下列命题中 : ①多边形每增加一条边 , 其内角和增加 180°; ②任意一个多边形的内角和一定是 180° 的整数倍 ; ③多边形的边数增加为原来的 2 倍 , 则多边形的内角和也增加为原来的 2 倍 ; ④任意两个多边形的内角和之差一定是 180° 的整数倍 . 其中 , 正确的是 ( 　　 ) A . ①② B . ①②④ C . ②④ D . ①②③④ [ 答案 ] B [ 答案 ] C 　 [ 解析 ] ∵在五边形 ABCDE 中 , ∠ A + ∠ B + ∠ E =300°, ∴∠ EDC + ∠ BCD =240° . 又∵ DP , CP 分别平分 ∠ EDC , ∠ BCD , ∴∠ PDC + ∠ PCD =120°, ∴在 △ CDP 中 , ∠ P =180°-( ∠ PDC + ∠ PCD )= 180°-120°=60° . 故选 C . 2 . [2018· 济宁 ] 如图 23-4, 在五边形 ABCDE 中 , ∠ A + ∠ B + ∠ E =300°, DP , CP 分别平分∠ EDC , ∠ BCD , 则∠ P =( 　　 ) A . 50° B . 55° C . 60° D . 65° 图 23-4 考向二　平行四边形的判定和性质 例 2 如图 23-5 ① , 在▱ ABCD 中 , 点 O 是对角线 AC 的中点 , EF 过点 O , 与 AD , BC 分别相交于点 E , F , GH 过点 O , 与 AB , CD 分别相交于点 G , H , 连接 EG , FG , FH , EH. (1) 求证 : 四边形 EGFH 是平行四边形 . (2) 如图② , 若 EF ∥ AB , GH ∥ BC , 在不添加任何辅助线的情况下 , 请直接写出图②中与四边形 AGHD 面积相等的所有平行四边形 ( 四边形 AGHD 除外 ) . 图 23-5 解 :(1) 证明 : ∵四边形 ABCD 为平行四边形 , ∴ AD ∥ BC , ∴∠ EAO = ∠ FCO. 又∵ OA = OC , ∠ AOE = ∠ COF , ∴ △ OAE ≌△ OCF , ∴ OE = OF. 同理可知 , OG = OH , ∴四边形 EGFH 是平行四边形 . 例 2 如图 23-5 ① , 在▱ ABCD 中 , 点 O 是对角线 AC 的中点 , EF 过点 O , 与 AD , BC 分别相交于点 E , F , GH 过点 O , 与 AB , CD 分别相交于点 G , H , 连接 EG , FG , FH , EH. (2) 如图② , 若 EF ∥ AB , GH ∥ BC , 在不添加任何辅助线的情况下 , 请直接写出图②中与四边形 AGHD 面积相等的所有平行四边形 ( 四边形 AGHD 除外 ) . 图 23-5 解 : (2) ▱ GBCH , ▱ ABFE , ▱ EFCD , ▱ EGFH. | 考向精练 | 1 . [2019· 广州 ] 如图 23-6, ▱ ABCD 中 , AB =2, AD =4, 对角线 AC , BD 相交于点 O , 且 E , F , G , H 分别是 AO , BO , CO , DO 的中点 , 则下列说法正确的是 ( 　　 ) A .EH = HG B . 四边形 EFGH 是平行四边形 C .AC ⊥ BD D . △ ABO 的面积是 △ EFO 的面积的 2 倍 图 23-6 [ 答案 ] B 2 . [2018· 安徽 ] 在▱ ABCD 中 , E , F 是对角线 BD 上不同的两点 , 下列条件中 , 不能得出四边形 AECF 一定为平行四边形的是 ( 　　 ) A .BE = DF B .AE = CF C .AF ∥ CE D . ∠ BAE = ∠ DCF [ 答案 ] B 　 [ 解析 ] 如图 , 连接 AC , 与 BD 相交于 O. 在▱ ABCD 中 , OA = OC , OB = OD , 要使四边形 AECF 为平行四边形 , 只需证明 OE = OF 即可 . A . 若 BE = DF , 则 OB - BE = OD - DF , 即 OE = OF , 故此选项不符合题意 ; B . 若 AE = CF , 无法判断 OE = OF , 故此选项符合题意 ; C . 由 AF ∥ CE 能够利用 “ 角角边 ” 证明 △ AOF 和 △ COE 全等 , 从而得到 OE = OF , 故此选项不符合题意 ; D . 由∠ BAE = ∠ DCF 能够利用 “ 角边角 ” 证明 △ ABE 和 △ CDF 全等 , 从而得到 DF = BE , 然后同 A, 故此选项不符合题意 . 故选 B . 3 . [2015· 鄂尔多斯 21 题 ] 如图 23-7, 在▱ ABCD 中 , E , F 分别为 AB , BC 的中点 , 连接 EC , AF , AF 与 EC 交于点 M , AF 的延长线与 DC 的延长线交于点 N. (1) 求证 : AB = CN. (2) 若 AB =2 n , BE =2 MF , 试用含 n 的式子表示线段 AN 的长 . 图 23-7 解 :(1) 证明 : ∵四边形 ABCD 是平行四边形 , ∴ AB ∥ DN , ∴∠ B = ∠ FCN , ∠ BAF = ∠ N. ∵ F 是 BC 的中点 , ∴ BF = CF , ∴ △ BAF ≌△ CNF , ∴ AB = CN. 3 . [2015· 鄂尔多斯 21 题 ] 如图 23-7, 在▱ ABCD 中 , E , F 分别为 AB , BC 的中点 , 连接 EC , AF , AF 与 EC 交于点 M , AF 的延长线与 DC 的延长线交于点 N. (2) 若 AB =2 n , BE =2 MF , 试用含 n 的式子表示线段 AN 的长 . 图 23-7 图 23-8 图 23-8