2019年江苏省宿迁市中考数学试卷含答案

2019年江苏省宿迁市中考数学试卷含答案

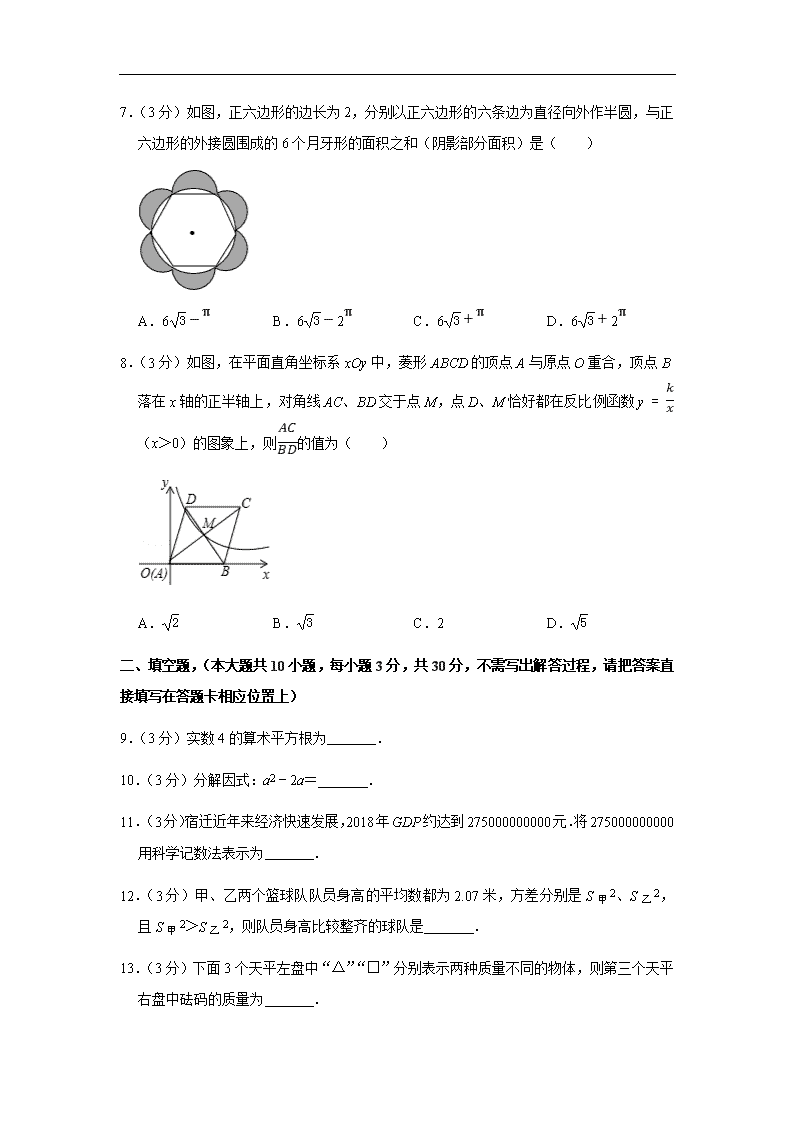
‎2019年江苏省宿迁市中考数学试卷 一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，有且只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）‎ ‎1．（3分）2019的相反数是（　　）‎ A．‎1‎‎2019‎ B．﹣2019 C．‎-‎‎1‎‎2019‎ D．2019‎ ‎2．（3分）下列运算正确的是（　　）‎ A．a2+a3＝a5 B．（a2）3＝a5 ‎ C．a6÷a3＝a2 D．（ab2）3＝a3b6‎ ‎3．（3分）一组数据：2、4、4、3、7、7，则这组数据的中位数是（　　）‎ A．3 B．3.5 C．4 D．7‎ ‎4．（3分）一副三角板如图摆放（直角顶点C重合），边AB与CE交于点F，DE∥BC，则∠BFC等于（　　）‎ A．105° B．100° C．75° D．60°‎ ‎5．（3分）一个圆锥的主视图如图所示，根据图中数据，计算这个圆锥的侧面积是（　　）‎ A．20π B．15π C．12π D．9π ‎6．（3分）不等式x﹣1≤2的非负整数解有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎7．（3分）如图，正六边形的边长为2，分别以正六边形的六条边为直径向外作半圆，与正六边形的外接圆围成的6个月牙形的面积之和（阴影部分面积）是（　　）‎ A．6‎3‎‎-‎π B．6‎3‎‎-‎2π C．6‎3‎‎+‎π D．6‎3‎‎+‎2π ‎8．（3分）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A与原点O重合，顶点B落在x轴的正半轴上，对角线AC、BD交于点M，点D、M恰好都在反比例函数y‎=‎kx（x＞0）的图象上，则ACBD的值为（　　）‎ A．‎2‎ B．‎3‎ C．2 D．‎‎5‎ 二、填空题，（本大题共10小题，每小题3分，共30分，不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．（3分）实数4的算术平方根为　 　．‎ ‎10．（3分）分解因式：a2﹣2a＝　 　．‎ ‎11．（3分）宿迁近年来经济快速发展，2018年GDP约达到275000000000元．将275000000000用科学记数法表示为　 　．‎ ‎12．（3分）甲、乙两个篮球队队员身高的平均数都为2.07米，方差分别是S甲2、S乙2，且S甲2＞S乙2，则队员身高比较整齐的球队是　 　．‎ ‎13．（3分）下面3个天平左盘中“△”“□”分别表示两种质量不同的物体，则第三个天平右盘中砝码的质量为　 　．‎ ‎14．（3分）抛掷一枚质地均匀的骰子一次，朝上一面的点数是3的倍数的概率是　 　．‎ ‎15．（3分）直角三角形的两条直角边分别是5和12，则它的内切圆半径为　 　．‎ ‎16．（3分）关于x的分式方程‎1‎x-2‎‎+a-2‎‎2-x=‎1的解为正数，则a的取值范围是　 　．‎ ‎17．（3分）如图，∠MAN＝60°，若△ABC的顶点B在射线AM上，且AB＝2，点C在射线AN上运动，当△ABC是锐角三角形时，BC的取值范围是　 　．‎ ‎18．（3分）如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为　 　．‎ 三、解答题（本大题共10题，共96分，请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（8分）计算：（‎1‎‎2‎）﹣1﹣（π﹣1）0+|1‎-‎‎3‎|．‎ ‎20．（8分）先化简，再求值：（1‎+‎‎1‎a-1‎）‎÷‎‎2aa‎2‎‎-1‎，其中a＝﹣2．‎ ‎21．（8分）如图，一次函数y＝kx+b的图象与反比例函数y‎=-‎‎5‎x的图象相交于点A（﹣1，m ‎）、B（n，﹣1）两点．‎ ‎（1）求一次函数表达式；‎ ‎（2）求△AOB的面积．‎ ‎22．（8分）如图，矩形ABCD中，AB＝4，BC＝2，点E、F分别在AB、CD上，且BE＝DF‎=‎‎3‎‎2‎．‎ ‎（1）求证：四边形AECF是菱形；‎ ‎（2）求线段EF的长．‎ ‎23．（10分）为了解学生的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图．‎ 男、女生所选类别人数统计表 ‎ 类别 男生（人）‎ 女生（人）‎ 文学类 ‎12‎ ‎8‎ 史学类 m ‎5‎ 科学类 ‎6‎ ‎5‎ 哲学类 ‎2‎ n 根据以上信息解决下列问题 ‎（1）m＝　 　，n＝　 　；‎ ‎（2）扇形统计图中“科学类”所对应扇形圆心角度数为　 　°；‎ ‎（3）从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率．‎ ‎24．（10分）在Rt△ABC中，∠C＝90°．‎ ‎（1）如图①，点O在斜边AB上，以点O为圆心，OB长为半径的圆交AB于点D，交BC于点E，与边AC相切于点F．求证：∠1＝∠2；‎ ‎（2）在图②中作⊙M，使它满足以下条件：‎ ‎①圆心在边AB上；②经过点B；③与边AC相切．‎ ‎（尺规作图，只保留作图痕迹，不要求写出作法）‎ ‎25．（10分）宿迁市政府为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面上的实物图，图②是其示意图，其中AB、CD都与地面l 平行，车轮半径为32cm，∠BCD＝64°，BC＝60cm，坐垫E与点B的距离BE为15cm．‎ ‎（1）求坐垫E到地面的距离；‎ ‎（2）根据经验，当坐垫E到CD的距离调整为人体腿长的0.8时，坐骑比较舒适．小明的腿长约为80cm，现将坐垫E调整至坐骑舒适高度位置E'，求EE′的长．‎ ‎（结果精确到0.1cm，参考数据：sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）‎ ‎26．（10分）超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加x元，每天售出y件．‎ ‎（1）请写出y与x之间的函数表达式；‎ ‎（2）当x为多少时，超市每天销售这种玩具可获利润2250元？‎ ‎（3）设超市每天销售这种玩具可获利w元，当x为多少时w最大，最大值是多少？‎ ‎27．（12分）如图①，在钝角△ABC中，∠ABC＝30°，AC＝4，点D为边AB中点，点E为边BC中点，将△BDE绕点B逆时针方向旋转α度（0≤α≤180）．‎ ‎（1）如图②，当0＜α＜180时，连接AD、CE．求证：△BDA∽△BEC；‎ ‎（2）如图③，直线CE、AD交于点G．在旋转过程中，∠AGC的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；‎ ‎（3）将△BDE从图①位置绕点B逆时针方向旋转180°，求点G的运动路程．‎ ‎28．（12分）如图，抛物线y＝x2+bx+c交x轴于A、B两点，其中点A坐标为（1，0），与y轴交于点C（0，﹣3）．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）如图①，连接AC，点P在抛物线上，且满足∠PAB＝2∠ACO．求点P的坐标；‎ ‎（3）如图②，点Q为x轴下方抛物线上任意一点，点D是抛物线对称轴与x轴的交点，直线AQ、BQ分别交抛物线的对称轴于点M、N．请问DM+DN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．‎ ‎2019年江苏省宿迁市中考数学试卷 参考答案与试题解析 一、选择题（本大题共8小题，每小题3分，共24分．在每小题所给出的四个选项中，有且只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）‎ ‎1．（3分）2019的相反数是（　　）‎ A．‎1‎‎2019‎ B．﹣2019 C．‎-‎‎1‎‎2019‎ D．2019‎ ‎【解答】解：2019的相反数是﹣2019．‎ 故选：B．‎ ‎2．（3分）下列运算正确的是（　　）‎ A．a2+a3＝a5 B．（a2）3＝a5 ‎ C．a6÷a3＝a2 D．（ab2）3＝a3b6‎ ‎【解答】解：A、a2+a3，无法计算，故此选项错误；‎ B、（a2）3＝a6，故此选项错误；‎ C、a6÷a3＝a3，故此选项错误；‎ D、（ab2）3＝a3b6，正确；‎ 故选：D．‎ ‎3．（3分）一组数据：2、4、4、3、7、7，则这组数据的中位数是（　　）‎ A．3 B．3.5 C．4 D．7‎ ‎【解答】解：这组数据重新排列为：2、3、4、4、7、7，‎ ‎∴这组数据的中位数为‎4+4‎‎2‎‎=‎4，‎ 故选：C．‎ ‎4．（3分）一副三角板如图摆放（直角顶点C重合），边AB与CE交于点F，DE∥BC ‎，则∠BFC等于（　　）‎ A．105° B．100° C．75° D．60°‎ ‎【解答】解：由题意知∠E＝45°，∠B＝30°，‎ ‎∵DE∥CB，‎ ‎∴∠BCF＝∠E＝45°，‎ 在△CFB中，‎ ‎∠BFC＝180°﹣∠B﹣∠BCF＝180°﹣30°﹣45°＝105°，‎ 故选：A．‎ ‎5．（3分）一个圆锥的主视图如图所示，根据图中数据，计算这个圆锥的侧面积是（　　）‎ A．20π B．15π C．12π D．9π ‎【解答】解：由勾股定理可得：底面圆的半径‎=‎5‎‎2‎‎-‎‎4‎‎2‎=3‎，则底面周长＝6π，底面半径＝3，‎ 由图得，母线长＝5，‎ 侧面面积‎=‎1‎‎2‎×‎6π×5＝15π．‎ 故选：B．‎ ‎6．（3分）不等式x﹣1≤2的非负整数解有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【解答】解：x﹣1≤2，‎ 解得：x≤3，‎ 则不等式x﹣1≤2的非负整数解有：0，1，2，3共4个．‎ 故选：D．‎ ‎7．（3分）如图，正六边形的边长为2，分别以正六边形的六条边为直径向外作半圆，与正六边形的外接圆围成的6个月牙形的面积之和（阴影部分面积）是（　　）‎ A．6‎3‎‎-‎π B．6‎3‎‎-‎2π C．6‎3‎‎+‎π D．6‎3‎‎+‎2π ‎【解答】解：6个月牙形的面积之和＝3π﹣（22π﹣6‎×‎1‎‎2‎×‎2‎×‎‎3‎）＝6‎3‎‎-‎π，‎ 故选：A．‎ ‎8．（3分）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A与原点O重合，顶点B落在x轴的正半轴上，对角线AC、BD交于点M，点D、M恰好都在反比例函数y‎=‎kx（x＞0）的图象上，则ACBD的值为（　　）‎ A．‎2‎ B．‎3‎ C．2 D．‎‎5‎ ‎【解答】解：设D（m，km），B（t，0），‎ ‎∵M点为菱形对角线的交点，‎ ‎∴BD⊥AC，AM＝CM，BM＝DM，‎ ‎∴M（m+t‎2‎，k‎2m），‎ 把M（m+t‎2‎，k‎2m）代入y‎=‎kx得m+t‎2‎•k‎2m‎=‎k，‎ ‎∴t＝3m，‎ ‎∵四边形ABCD为菱形，‎ ‎∴OD＝AB＝t，‎ ‎∴m2+（km）2＝（3m）2，解得k＝2‎2‎m2，‎ ‎∴M（2m，‎2‎m），‎ 在Rt△ABM中，tan∠MAB‎=BMAM=‎2‎m‎2m=‎‎1‎‎2‎，‎ ‎∴ACBD‎=‎‎2‎．‎ 故选：A．‎ 二、填空题，（本大题共10小题，每小题3分，共30分，不需写出解答过程，请把答案直接填写在答题卡相应位置上）‎ ‎9．（3分）实数4的算术平方根为　2　．‎ ‎【解答】解：∵22＝4，‎ ‎∴4的算术平方根是2．‎ 故答案为：2．‎ ‎10．（3分）分解因式：a2﹣2a＝　a（a﹣2）　．‎ ‎【解答】解：a2﹣2a＝a（a﹣2）．‎ 故答案为：a（a﹣2）．‎ ‎11．（3分）宿迁近年来经济快速发展，2018年GDP约达到275000000000元．将275000000000用科学记数法表示为　2.75×1011　．‎ ‎【解答】解：将275000000000用科学记数法表示为：2.75×1011．‎ 故答案为：2.75×1011．‎ ‎12．（3分）甲、乙两个篮球队队员身高的平均数都为2.07米，方差分别是S甲2、S乙2，且S甲2＞S乙2，则队员身高比较整齐的球队是　乙　．‎ ‎【解答】解：∵S甲2＞S乙2，‎ ‎∴队员身高比较整齐的球队是乙，‎ 故答案为：乙．‎ ‎13．（3分）下面3个天平左盘中“△”“□”分别表示两种质量不同的物体，则第三个天平右盘中砝码的质量为　10　．‎ ‎【解答】解：设“△”的质量为x，“□”的质量为y，‎ 由题意得：x+y=6‎x+2y=8‎，‎ 解得：x=4‎y=2‎，‎ ‎∴第三个天平右盘中砝码的质量＝2x+y＝2×4+2＝10；‎ 故答案为：10．‎ ‎14．（3分）抛掷一枚质地均匀的骰子一次，朝上一面的点数是3的倍数的概率是　‎1‎‎3‎　．‎ ‎【解答】解：∵骰子的六个面上分别刻有1到6的点数，点数为3的倍数的有2个，‎ ‎∴掷得朝上一面的点数为3的倍数的概率为：‎2‎‎6‎‎=‎‎1‎‎3‎．‎ 故答案为：‎1‎‎3‎．‎ ‎15．（3分）直角三角形的两条直角边分别是5和12，则它的内切圆半径为　2　．‎ ‎【解答】解：直角三角形的斜边‎=‎5‎‎2‎‎+1‎‎2‎‎2‎=‎13，‎ 所以它的内切圆半径‎=‎5+12-13‎‎2‎=‎2．‎ 故答案为2．‎ ‎16．（3分）关于x的分式方程‎1‎x-2‎‎+a-2‎‎2-x=‎1的解为正数，则a的取值范围是　a＜5且a≠3　．‎ ‎【解答】解：去分母得：1﹣a+2＝x﹣2，‎ 解得：x＝5﹣a，‎ ‎5﹣a＞0，‎ 解得：a＜5，‎ 当x＝5﹣a＝2时，a＝3不合题意，‎ 故a＜5且a≠3．‎ 故答案为：a＜5且a≠3．‎ ‎17．（3分）如图，∠MAN＝60°，若△ABC的顶点B在射线AM上，且AB＝2，点C在射线AN上运动，当△ABC是锐角三角形时，BC的取值范围是　‎3‎‎＜‎BC‎＜2‎‎3‎　．‎ ‎【解答】解：如图，过点B作BC1⊥AN，垂足为C1，BC2⊥AM，交AN于点C2‎ 在Rt△ABC1中，AB＝2，∠A＝60°‎ ‎∴∠ABC1＝30°‎ ‎∴AC1‎=‎‎1‎‎2‎AB＝1，由勾股定理得：BC1‎=‎‎3‎，‎ 在Rt△ABC2中，AB＝2，∠A＝60°‎ ‎∴∠AC2B＝30°‎ ‎∴AC2＝4，由勾股定理得：BC2＝2‎3‎，‎ 当△ABC是锐角三角形时，点C在C1C2上移动，此时‎3‎‎＜‎BC＜2‎3‎．‎ 故答案为：‎3‎‎＜‎BC＜2‎3‎．‎ ‎18．（3分）如图，正方形ABCD的边长为4，E为BC上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为　‎5‎‎2‎　．‎ ‎【解答】解：由题意可知，点F是主动点，点G是从动点，点F在线段上运动，点G也一定在直线轨迹上运动 将△EFB绕点E旋转60°，使EF与EG重合，得到△EFB≌△EHG 从而可知△EBH为等边三角形，点G在垂直于HE的直线HN上 作CM⊥HN，则CM即为CG的最小值 作EP⊥CM，可知四边形HEPM为矩形，‎ 则CM＝MP+CP＝HE‎+‎‎1‎‎2‎EC＝1‎‎+‎3‎‎2‎=‎‎5‎‎2‎ 故答案为‎5‎‎2‎．‎ 三、解答题（本大题共10题，共96分，请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）‎ ‎19．（8分）计算：（‎1‎‎2‎）﹣1﹣（π﹣1）0+|1‎-‎‎3‎|．‎ ‎【解答】解：原式＝2﹣1‎+‎3‎-‎1‎ ‎=‎‎3‎‎．‎ ‎20．（8分）先化简，再求值：（1‎+‎‎1‎a-1‎）‎÷‎‎2aa‎2‎‎-1‎，其中a＝﹣2．‎ ‎【解答】解：原式‎=aa-1‎×‎‎(a+1)(a-1)‎‎2a ‎=‎a+1‎‎2‎‎，‎ 当a＝﹣2时，原式‎=‎-2+1‎‎2‎=-‎‎1‎‎2‎．‎ ‎21．（8分）如图，一次函数y＝kx+b的图象与反比例函数y‎=-‎‎5‎x的图象相交于点A（﹣1，m）、B（n，﹣1）两点．‎ ‎（1）求一次函数表达式；‎ ‎（2）求△AOB的面积．‎ ‎【解答】解：（1）把A（﹣1．m），B（n，﹣1）代入y‎=-‎‎5‎x，得m＝5，n＝5，‎ ‎∴A（﹣1，5），B（5，﹣1），‎ 把A（﹣1，5），B（5，﹣1）代入y＝kx+b得 ‎-k+b=5‎‎5k+b=-1‎‎，解得k=-1‎b=4‎，‎ ‎∴一次函数解析式为y＝﹣x+4；‎ ‎（2）x＝0时，y＝4，‎ ‎∴OD＝4，‎ ‎∴△AOB的面积＝S△AOD+S△BOD‎=‎1‎‎2‎×‎4×1‎+‎1‎‎2‎×4×5=‎12．‎ ‎22．（8分）如图，矩形ABCD中，AB＝4，BC＝2，点E、F分别在AB、CD上，且BE＝DF‎=‎‎3‎‎2‎．‎ ‎（1）求证：四边形AECF是菱形；‎ ‎（2）求线段EF的长．‎ ‎【解答】（1）证明：∵在矩形ABCD中，AB＝4，BC＝2，‎ ‎∴CD＝AB＝4，AD＝BD＝2，CD∥AB，∠D＝∠B＝90°，‎ ‎∵BE＝DF‎=‎‎3‎‎2‎，‎ ‎∴CF＝AE＝4‎-‎3‎‎2‎=‎‎5‎‎2‎，‎ ‎∴AF＝CE‎=‎2‎‎2‎‎+(‎‎3‎‎2‎‎)‎‎2‎=‎‎5‎‎2‎，‎ ‎∴AF＝CF＝CE＝AE‎=‎‎5‎‎2‎，‎ ‎∴四边形AECF是菱形；‎ ‎（2）解：过F作FH⊥AB于H，‎ 则四边形AHFD是矩形，‎ ‎∴AH＝DF‎=‎‎3‎‎2‎，FH＝AD＝2，‎ ‎∴EH‎=‎5‎‎2‎-‎3‎‎2‎=‎1，‎ ‎∴EF‎=FH‎2‎+HE‎2‎=‎2‎‎2‎‎+‎‎1‎‎2‎=‎‎5‎．‎ ‎23．（10分）为了解学生的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图．‎ 男、女生所选类别人数统计表 ‎ 类别 男生（人）‎ 女生（人）‎ 文学类 ‎12‎ ‎8‎ 史学类 m ‎5‎ 科学类 ‎6‎ ‎5‎ 哲学类 ‎2‎ n 根据以上信息解决下列问题 ‎（1）m＝　20　，n＝　2　；‎ ‎（2）扇形统计图中“科学类”所对应扇形圆心角度数为　79.2　°；‎ ‎（3）从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率．‎ ‎【解答】解：（1）抽查的总学生数是：（12+8）÷40%＝50（人），‎ m＝50×30%﹣5＝10，n＝50﹣20﹣15﹣11﹣2＝2；‎ 故答案为：20，2；‎ ‎（2）扇形统计图中“科学类”所对应扇形圆心角度数为360°‎×‎6+5‎‎50‎=‎79.2°；‎ 故答案为：79.2；‎ ‎（3）列表得：‎ 男1‎ 男2‎ 女1‎ 女2‎ 男1‎ ‎﹣﹣‎ 男2男1‎ 女1男1‎ 女2男1‎ 男2‎ 男1男2‎ ‎﹣﹣‎ 女1男2‎ 女2男2‎ 女1‎ 男1女1‎ 男2女1‎ ‎﹣﹣‎ 女2女1‎ 女2‎ 男1女2‎ 男2女2‎ 女1女2‎ ‎﹣﹣‎ 由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中所选取的两名学生都是男生的有2种可能，‎ ‎∴所选取的两名学生都是男生的概率为‎2‎‎12‎‎=‎‎1‎‎6‎．‎ ‎24．（10分）在Rt△ABC中，∠C＝90°．‎ ‎（1）如图①，点O在斜边AB上，以点O为圆心，OB长为半径的圆交AB于点D，交BC于点E，与边AC相切于点F．求证：∠1＝∠2；‎ ‎（2）在图②中作⊙M，使它满足以下条件：‎ ‎①圆心在边AB上；②经过点B；③与边AC相切．‎ ‎（尺规作图，只保留作图痕迹，不要求写出作法）‎ ‎【解答】解：（1）证明：如图①，连接OF，‎ ‎∵AC是⊙O的切线，‎ ‎∴OE⊥AC，‎ ‎∵∠C＝90°，‎ ‎∴OE∥BC，‎ ‎∴∠1＝∠OFB，‎ ‎∵OF＝OB，‎ ‎∴∠OFB＝∠2，‎ ‎∴∠1＝∠2．‎ ‎（2）如图②所示⊙M为所求．①‎ ‎①作∠ABC平分线交AC于F点，‎ ‎②作BF的垂直平分线交AB于M，以MB为半径作圆，‎ 即⊙M为所求．‎ 证明：∵M在BF的垂直平分线上，‎ ‎∴MF＝MB，‎ ‎∴∠MBF＝∠MFB，‎ 又∵BF平分∠ABC，‎ ‎∴∠MBF＝∠CBF，‎ ‎∴∠CBF＝∠MFB，‎ ‎∴MF∥BC，‎ ‎∵∠C＝90°，‎ ‎∴FM⊥AC，‎ ‎∴⊙M与边AC相切．‎ ‎25．（10分）宿迁市政府为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面上的实物图，图②是其示意图，其中AB、CD都与地面l平行，车轮半径为32cm，∠BCD＝64°，BC＝60cm，坐垫E与点B的距离BE为15cm．‎ ‎（1）求坐垫E到地面的距离；‎ ‎（2）根据经验，当坐垫E到CD的距离调整为人体腿长的0.8时，坐骑比较舒适．小明的腿长约为80cm，现将坐垫E调整至坐骑舒适高度位置E'，求EE′的长．‎ ‎（结果精确到0.1cm，参考数据：sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）‎ ‎【解答】解：（1）如图1，过点E作EM⊥CD于点M，‎ 由题意知∠BCM＝64°、EC＝BC+BE＝60+15＝75cm，‎ ‎∴EM＝ECsin∠BCM＝75sin64°≈67.5（cm），‎ 则单车车座E到地面的高度为67.5+32≈99.5（cm）；‎ ‎（2）如图2所示，过点E′作E′H⊥CD于点H，‎ 由题意知E′H＝80×0.8＝64，‎ 则E′C‎=E'Hsin∠ECH=‎64‎sin64°‎≈‎71，1，‎ ‎∴EE′＝CE﹣CE′＝75﹣71.1＝3.9（cm）．‎ ‎26．（10分）超市销售某种儿童玩具，如果每件利润为40元（市场管理部门规定，该种玩具每件利润不能超过60元），每天可售出50件．根据市场调查发现，销售单价每增加2元，每天销售量会减少1件．设销售单价增加x元，每天售出y件．‎ ‎（1）请写出y与x之间的函数表达式；‎ ‎（2）当x为多少时，超市每天销售这种玩具可获利润2250元？‎ ‎（3）设超市每天销售这种玩具可获利w元，当x为多少时w最大，最大值是多少？‎ ‎【解答】解：（1）根据题意得，y‎=-‎‎1‎‎2‎x+50；‎ ‎（2）根据题意得，（40+x）（‎-‎‎1‎‎2‎x+50）＝2250，‎ 解得：x1＝50，x2＝10，‎ ‎∵每件利润不能超过60元，‎ ‎∴x＝10，‎ 答：当x为10时，超市每天销售这种玩具可获利润2250元；‎ ‎（3）根据题意得，w＝（40+x）（‎-‎‎1‎‎2‎x+50）‎=-‎‎1‎‎2‎x2+30x+2000‎=-‎‎1‎‎2‎（x﹣30）2+2450，‎ ‎∵a‎=-‎1‎‎2‎＜‎0，‎ ‎∴当x＜30时，w随x的增大而增大，‎ ‎∴当x＝20时，w增大＝2400，‎ 答：当x为20时w最大，最大值是2400元．‎ ‎27．（12分）如图①，在钝角△ABC中，∠ABC＝30°，AC＝4，点D为边AB中点，点E 为边BC中点，将△BDE绕点B逆时针方向旋转α度（0≤α≤180）．‎ ‎（1）如图②，当0＜α＜180时，连接AD、CE．求证：△BDA∽△BEC；‎ ‎（2）如图③，直线CE、AD交于点G．在旋转过程中，∠AGC的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；‎ ‎（3）将△BDE从图①位置绕点B逆时针方向旋转180°，求点G的运动路程．‎ ‎【解答】解：（1）如图②中，‎ 由图①，∵点D为边AB中点，点E为边BC中点，‎ ‎∴DE∥AC，‎ ‎∴BDBA‎=‎BEBC，‎ ‎∴BDBE‎=‎BABC，‎ ‎∵∠DBE＝∠ABC，‎ ‎∴∠DBA＝∠EBC，‎ ‎∴△DBA∽△EBC．‎ ‎（2）∠AGC的大小不发生变化，∠AGC＝30°．‎ 理由：如图③中，设AB交CG于点O．‎ ‎∵△DBA∽△EBC，‎ ‎∴∠DAB＝∠ECB，‎ ‎∵∠DAB+∠AOG+∠G＝180°，∠ECB+∠COB+∠ABC＝180°，∠AOG＝∠COB，‎ ‎∴∠G＝∠ABC＝30°．‎ ‎（3）如图③﹣1中．设AB的中点为K，连接DK，以AC为边向右作等边△ACO，连接OG，OB．‎ 以O为圆心，OA为半径作⊙O，‎ ‎∵∠AGC＝30°，∠AOC＝60°，‎ ‎∴∠AGC‎=‎‎1‎‎2‎∠AOC，‎ ‎∴点G在⊙O上运动，‎ 以B为圆心，BD为半径作⊙B，当直线与⊙B相切时，BD⊥AD，‎ ‎∴∠ADB＝90°，‎ ‎∵BK＝AK，‎ ‎∴DK＝BK＝AK，‎ ‎∵BD＝BK，‎ ‎∴BD＝DK＝BK，‎ ‎∴△BDK是等边三角形，‎ ‎∴∠DBK＝60°，‎ ‎∴∠DAB＝30°，‎ ‎∴∠DOG＝2∠DAB＝60°，‎ ‎∴BG的长‎=‎60⋅π⋅4‎‎180‎=‎‎4π‎3‎，‎ 观察图象可知，点G的运动路程是BG的长的两倍‎=‎‎8π‎3‎．‎ ‎28．（12分）如图，抛物线y＝x2+bx+c交x轴于A、B两点，其中点A坐标为（1，0），与y轴交于点C（0，﹣3）．‎ ‎（1）求抛物线的函数表达式；‎ ‎（2）如图①，连接AC，点P在抛物线上，且满足∠PAB＝2∠ACO．求点P的坐标；‎ ‎（3）如图②，点Q为x轴下方抛物线上任意一点，点D是抛物线对称轴与x轴的交点，直线AQ、BQ分别交抛物线的对称轴于点M、N．请问DM+DN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．‎ ‎【解答】解：（1）∵抛物线y＝x2+bx+c经过点A（1，0），C（0，﹣3）‎ ‎∴‎1+b+c=0‎‎0+0+c=-3‎ 解得：‎b=2‎c=-3‎ ‎∴抛物线的函数表达式为y＝x2+2x﹣3‎ ‎（2）①若点P在x轴下方，如图1，‎ 延长AP到H，使AH＝AB，过点B作BI⊥x轴，连接BH，作BH中点G，连接并延长AG交BI于点F，过点H作HI⊥BI于点I ‎∵当x2+2x﹣3＝0，解得：x1＝﹣3，x2＝1‎ ‎∴B（﹣3，0）‎ ‎∵A（1，0），C（0，﹣3）‎ ‎∴OA＝1，OC＝3，AC‎=‎1‎‎2‎‎+‎‎3‎‎2‎=‎‎10‎，AB＝4‎ ‎∴Rt△AOC中，sin∠ACO‎=OAAC=‎‎10‎‎10‎，cos∠ACO‎=OCAC=‎‎3‎‎10‎‎10‎ ‎∵AB＝AH，G为BH中点 ‎∴AG⊥BH，BG＝GH ‎∴∠BAG＝∠HAG，即∠PAB＝2∠BAG ‎∵∠PAB＝2∠ACO ‎∴∠BAG＝∠ACO ‎∴Rt△ABG中，∠AGB＝90°，sin∠BAG‎=BGAB=‎‎10‎‎10‎ ‎∴BG‎=‎‎10‎‎10‎AB‎=‎‎2‎‎10‎‎5‎ ‎∴BH＝2BG‎=‎‎4‎‎10‎‎5‎ ‎∵∠HBI+∠ABG＝∠ABG+∠BAG＝90°‎ ‎∴∠HBI＝∠BAG＝∠ACO ‎∴Rt△BHI中，∠BIH＝90°，sin∠HBI‎=HIBH=‎‎10‎‎10‎，cos∠HBI‎=BIBH=‎‎3‎‎10‎‎10‎ ‎∴HI‎=‎‎10‎‎10‎BH‎=‎‎4‎‎5‎，BI‎=‎‎3‎‎10‎‎10‎BH‎=‎‎12‎‎5‎ ‎∴xH＝﹣3‎+‎4‎‎5‎=-‎‎11‎‎5‎，yH‎=-‎‎12‎‎5‎，即H（‎-‎‎11‎‎5‎，‎-‎‎12‎‎5‎）‎ 设直线AH解析式为y＝kx+a ‎∴k+a=0‎‎-‎11‎‎5‎k+a=-‎‎12‎‎5‎ 解得：‎k=‎‎3‎‎4‎a=-‎‎3‎‎4‎ ‎∴直线AH：y‎=‎‎3‎‎4‎x‎-‎‎3‎‎4‎ ‎∵y=‎3‎‎4‎x-‎‎3‎‎4‎y=x‎2‎+2x-3‎ 解得：x‎1‎‎=1‎y‎1‎‎=0‎（即点A），‎x‎2‎‎=-‎‎9‎‎4‎y‎2‎‎=-‎‎39‎‎16‎ ‎∴P（‎-‎‎9‎‎4‎，‎-‎‎39‎‎16‎）‎ ‎②若点P在x轴上方，如图2，‎ 在AP上截取AH'＝AH，则H'与H关于x轴对称 ‎∴H'（‎-‎‎11‎‎5‎，‎12‎‎5‎）‎ 设直线AH'解析式为y＝k'x+a'‎ ‎∴k'+a'=0‎‎-‎11‎‎5‎k'+a'=‎‎12‎‎5‎ 解得：‎k'=-‎‎3‎‎4‎a'=‎‎3‎‎4‎ ‎∴直线AH'：y‎=-‎‎3‎‎4‎x‎+‎‎3‎‎4‎ ‎∵y=-‎3‎‎4‎x+‎‎3‎‎4‎y=x‎2‎+2x-3‎ 解得：x‎1‎‎=1‎y‎1‎‎=0‎（即点A），‎x‎2‎‎=-‎‎15‎‎4‎y‎2‎‎=‎‎57‎‎16‎ ‎∴P（‎-‎‎15‎‎4‎，‎57‎‎16‎）‎ 综上所述，点P的坐标为（‎-‎‎9‎‎4‎，‎-‎‎39‎‎16‎）或（‎-‎‎15‎‎4‎，‎57‎‎16‎）．‎ ‎（3）DM+DN为定值 ‎∵抛物线y＝x2+2x﹣3的对称轴为：直线x＝﹣1‎ ‎∴D（﹣1，0），xM＝xN＝﹣1‎ 设Q（t，t2+2t﹣3）（﹣3＜t＜1）‎ 设直线AQ解析式为y＝dx+e ‎∴d+e=0‎dt+e=t‎2‎+2t-3‎ 解得：‎d=t+3‎e=-t-3‎ ‎∴直线AQ：y＝（t+3）x﹣t﹣3‎ 当x＝﹣1时，yM＝﹣t﹣3﹣t﹣3＝﹣2t﹣6‎ ‎∴DM＝0﹣（﹣2t﹣6）＝2t+6‎ 设直线BQ解析式为y＝mx+n ‎∴‎-3m+n-0‎mt+n=t‎2‎+2t-3‎ 解得：‎m=t-1‎n=3t-3‎ ‎∴直线BQ：y＝（t﹣1）x+3t﹣3‎ 当x＝﹣1时，yN＝﹣t+1+3t﹣3＝2t﹣2‎ ‎∴DN＝0﹣（2t﹣2）＝﹣2t+2‎ ‎∴DM+DN＝2t+6+（﹣2t+2）＝8，为定值．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:57:39；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎