- 2021-11-06 发布 |
- 37.5 KB |
- 3页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级下册数学教案32-2 第2课时 较复杂几何体的三视图 冀教版
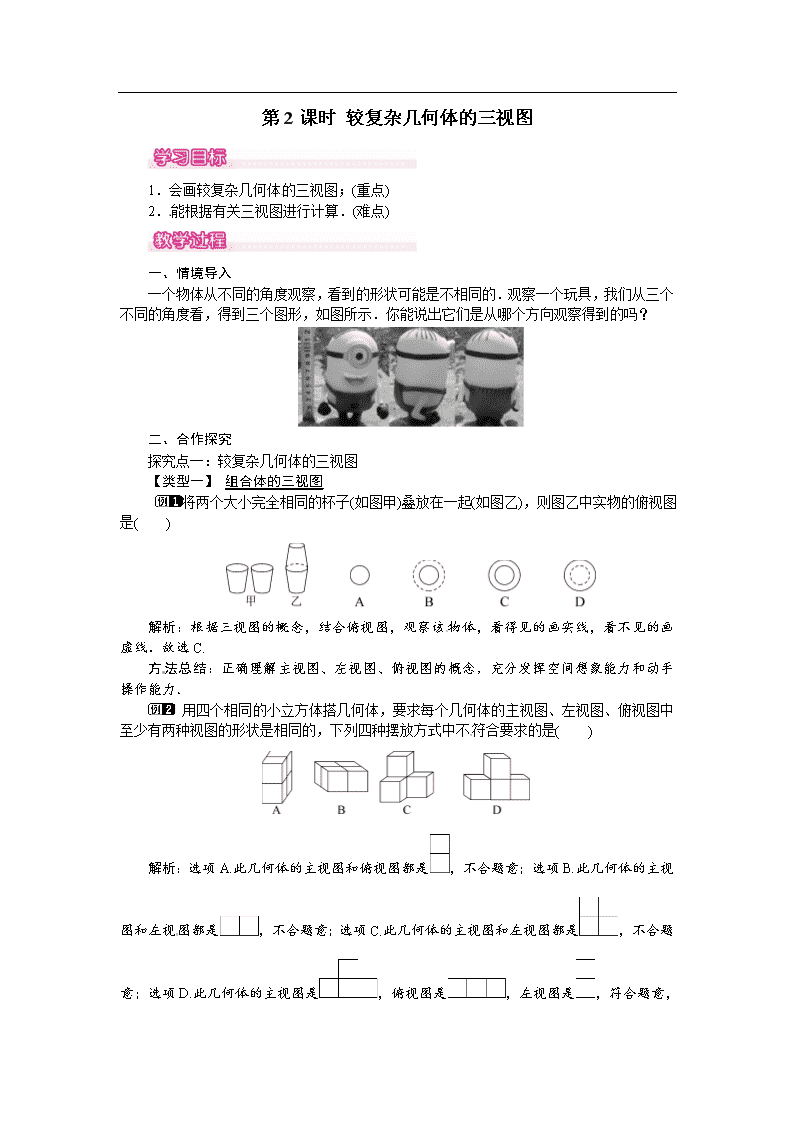
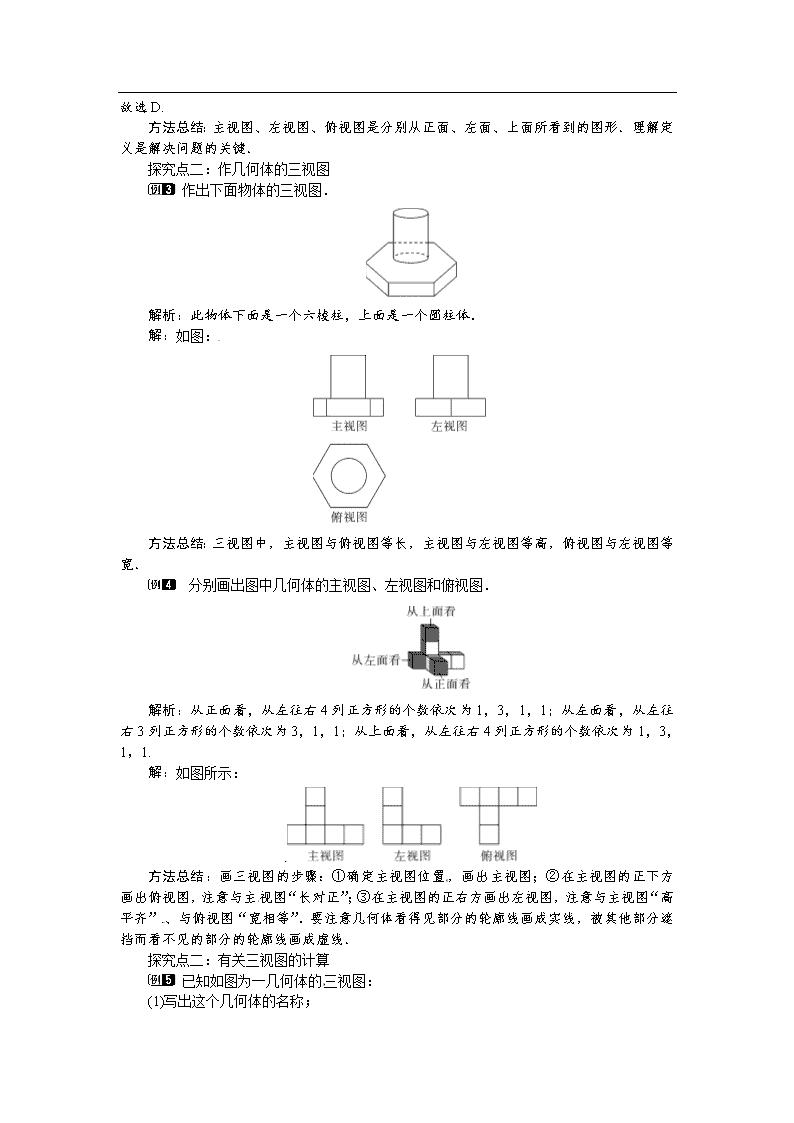
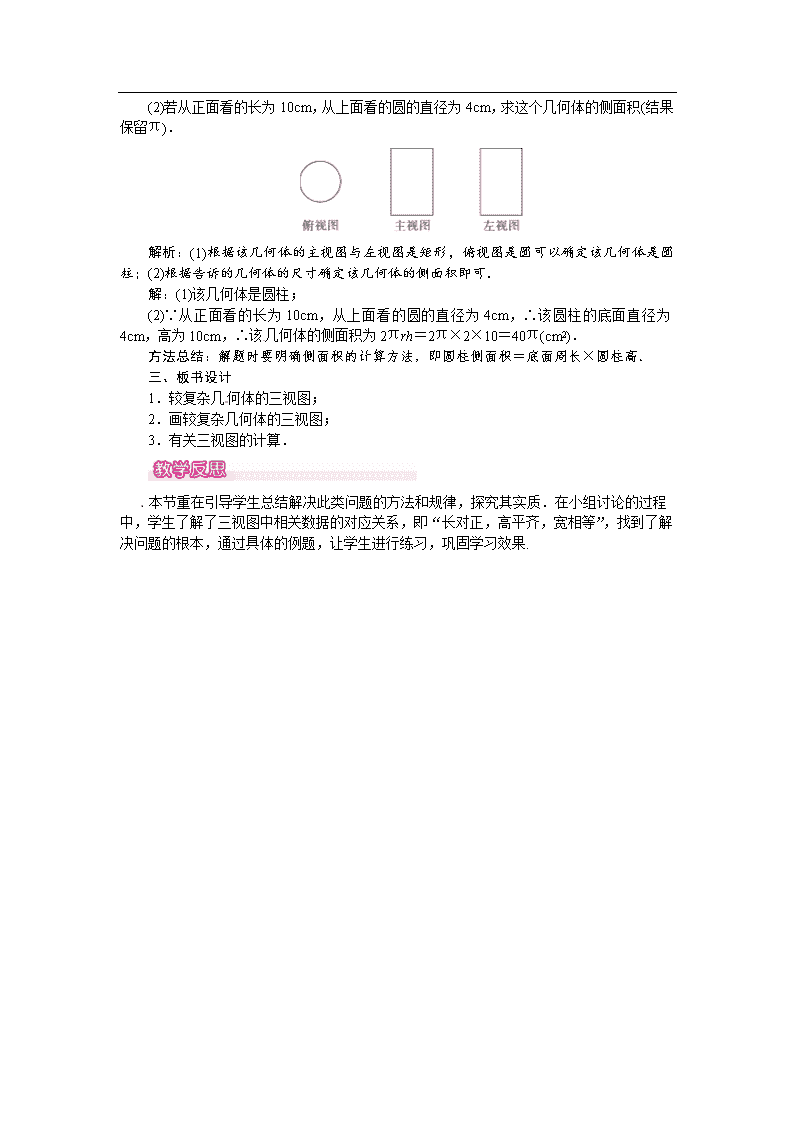
第2课时 较复杂几何体的三视图 1.会画较复杂几何体的三视图;(重点) 2.能根据有关三视图进行计算.(难点) [来源:学科网ZXXK] 一、情境导入 一个物体从不同的角度观察,看到的形状可能是不相同的.观察一个玩具,我们从三个不同的角度看,得到三个图形,如图所示.你能说出它们是从哪个方向观察得到的吗? 二、 合作探究 探究点一:较复杂几何体的三视图 【类型一】 组合体的三视图 将两个大小完全相同的杯子(如图甲)叠放在一起(如图乙),则图乙中实物的俯视图是( ) 解析:根据三视图的概念,结合俯视图,观察该物体,看得见的画实线,看不见的画虚线.故选C. 方法总结:正确理解主视图、左视图、俯视图的概念,充分发挥空间想象能力和动手操作能力. 用四个相同的小立方体搭几何体,要求每个几何体的主视图、左视图、俯视图中至少有两种视图的形状是相同的,下列四种摆放方式中不符合要求的是( ) [来源:学*科*网Z*X*X*K] 解析:选项A.此几何体的主视图和俯视图都是,不合题意;选项B.此几何体的主视图和左视图都是,不合题意;选项C.此几何体的主视图和左视图都是,不合题意;选项D.此几何体的主视图是,俯视图是,左视图是,符合题意, 故选D. 方法总结:主视图、左视图、俯视图是分别从正面、左面、上面所看到的图形.理解定义是解决问题的关键. 探究点二:作几何体的三视图 作出下面物体的三视图. 解析:此物体下面是一个六棱柱,上面是一个圆柱体. 解:如图: [来源:学科网ZXXK] 方法总结:三视图中,主视图与俯视图等长,主视图与左视图等高,俯视图与左视图等宽. 分别画出图中几何体的主视图、左视图和俯视图. 解析:从正面看,从左往右4列正方形的个数依次为1,3,1,1;从左面看,从左往右3列正方形的个数依次为3,1,1;从上面看,从左往右4列正方形的个数依次为1,3,1,1. 解:如图所示: 方法总结:画三视图的步骤:①确定主视图位置,画出主视图;②在主视图的正下方画出俯视图,注意与主视图“长对正”;③在主视图的正右方画出左视图,注意与主视图“高平齐”、与俯视图“宽相等”.要注意几何体看得见部分的轮廓线画成实线,被其他部分遮挡而看不见的部分的轮廓线画成虚线. 探究点二:有关三视图的计算[来源:Zxxk.Com] 已知如图为一几何体的三视图: (1)写出这个几何体的名称; (2)若从正面看的长为10cm,从上面看的圆的直径为4cm,求这个几何体的侧面积(结果保留π). 解析:(1)根据该几何体的主视图与左视图是矩形,俯视图是圆可以确定该几何体是圆柱;(2)根据告诉的几何体的尺寸确定该几何体的侧面积即可. 解:(1)该几何体是圆柱; (2)∵从正面看的长为10cm,从上面看的圆的直径为4cm,∴该圆柱的底面直径为4cm,高为10cm,∴该几何体的侧面积为2πrh=2π×2×10=40π(cm2). 方法总结:解题时要明确侧面积的计算方法,即圆柱侧面积=底面周长×圆柱高.[来源:Zxxk.Com] 三、板书设计 1.较复杂几何体的三视图; 2.画较复杂几何体的三视图; 3.有关三视图的计算. 本节重在引导学生总结解决此类问题的方法和规律,探究其实质.在小组讨论的过程中,学生了解了三视图中相关数据的对应关系,即“长对正,高平齐,宽相等”,找到了解决问题的根本,通过具体的例题,让学生进行练习,巩固学习效果.查看更多