2020九年级数学下册 第3章 三视图与表面展开图 3

2020九年级数学下册 第3章 三视图与表面展开图 3

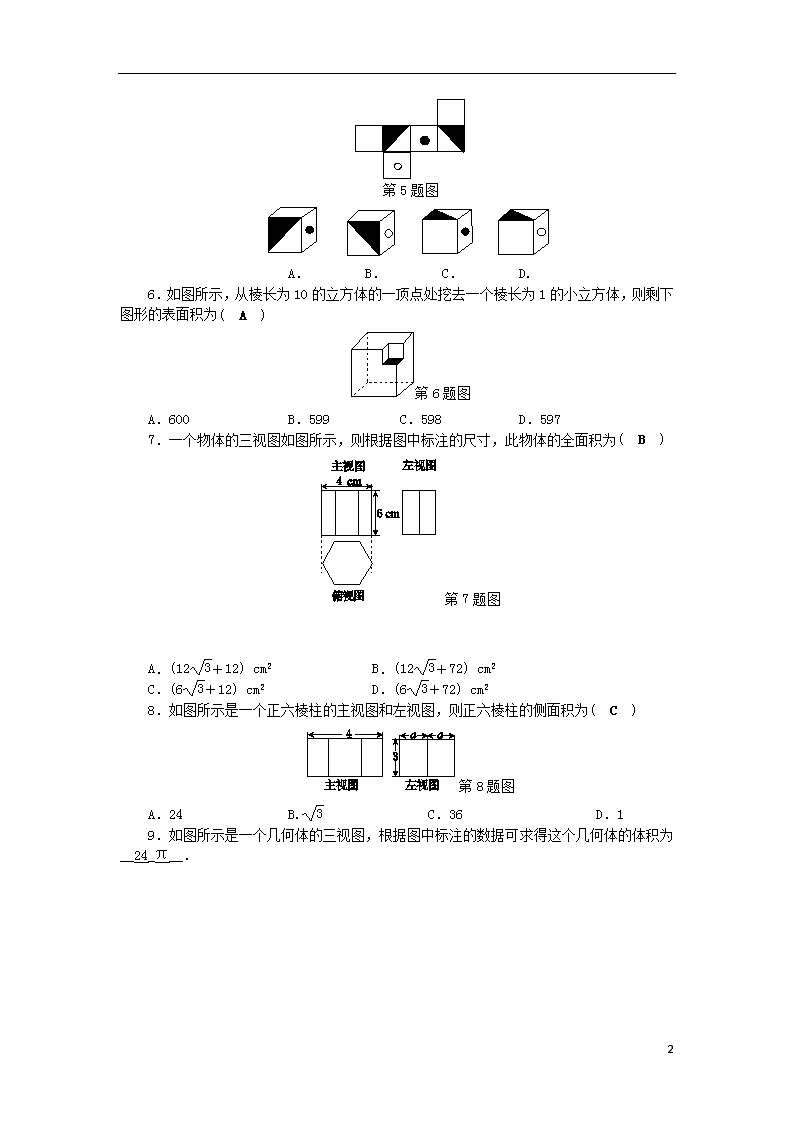
3.4 简单几何体的表面展开图(2)‎ ‎(见B本73页)‎ A　练就好基础　基础达标 ‎1．如图所示是某几何体的三视图，其侧面积为__6π__．‎ ‎2．用一个边长为‎4 cm的正方形折叠围成一个四棱柱的侧面，若该四棱柱的底面是一个正方形，则此正方形边长为__1__ cm.‎ ‎　 　　　　　　　　　 　　　 　　　　　‎ 第1题图 ‎　　第4题图 ‎3．用一个宽‎4 cm、长‎7cm的矩形卷成一个圆柱，则此圆柱的侧面积为__28_cm2__．‎ ‎4．如图所示是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度的取值范围为__12≤a≤13__．(罐壁的厚度和小圆孔的大小忽略不计)‎ ‎5．如图所示的展开图不可能拼成的立方体是(　B　)‎ 5‎ 第5题图 A．　　　　B．　　　　C．　　　　D.‎ ‎6．如图所示，从棱长为10的立方体的一顶点处挖去一个棱长为1的小立方体，则剩下图形的表面积为(　A　)‎ 第6题图 A．600 B．‎599 ‎ C．598 D．597‎ ‎7．一个物体的三视图如图所示，则根据图中标注的尺寸，此物体的全面积为(　B　)‎ 第7题图 A．(12＋12) cm2 B．(12＋72) cm2‎ C．(6＋12) cm2 D．(6＋72) cm2‎ ‎8．如图所示是一个正六棱柱的主视图和左视图，则正六棱柱的侧面积为(　C　)‎ 第8题图 A．24　　　 B.　　　 C．36　　　 D．1‎ ‎9．如图所示是一个几何体的三视图，根据图中标注的数据可求得这个几何体的体积为__24_π__．‎ 5‎ 第9题图 第10题图 ‎10．如图所示，有一个圆柱，底面圆的直径AB＝ cm，高BC＝‎12 cm，P为BC的中点，求蚂蚁从A点爬到P点的最短距离．‎ 第10题答图 解：圆柱的侧面展开图如图，‎ ‎∵圆柱底面直径AB＝ cm，高BC＝12 cm，P为BC的中点，‎ ‎∴圆柱底面圆的半径是 cm，BP＝6 cm，‎ ‎∴AB＝π×＝8 (cm)，‎ 在Rt△ABP中，AP＝＝10 (cm)．‎ 即蚂蚁从A点爬到P点的最短距离为10 cm.‎ B　更上一层楼　能力提升 ‎11．如图所示，透明的圆柱形容器(容器厚度忽略不计)的高为‎12 cm，底面周长为‎10 cm，在容器内壁离容器底部‎3 cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿‎3 cm的点A处，则蚂蚁吃到饭粒需爬行的最短路径是(　A　)‎ A．‎13 cm B．‎2 cm C. cm D．‎2 cm 第11题图 5‎ ‎　　　第12题图 ‎12．如图所示，在一个棱长为‎10 cm的立方体中挖去一个底面半径为‎3 cm的圆柱形小孔，这个物体的表面积约为__732__cm2.(保留整数)‎ ‎13．如图所示，已知矩形ABCD，AB＝‎2 cm，AD＝‎6 cm，求分别以AB，AD所在的直线为轴旋转后所得圆柱的侧面积．‎ 第13题图 解：依题意可知，分两种情况：‎ ‎(1)以AB所在的直线为轴旋转后所得圆柱的底面半径为BC，圆柱的底面周长为6×2π＝12π(cm)，侧面积为 12π×2＝24π(cm2)．‎ ‎(2)以AD所在的直线为轴旋转后所得圆柱的底面半径为AB，圆柱的底面周长为2×2π＝4π(cm)，侧面积为 4π×6＝24π(cm2)．‎ 所以以AB，AD所在直线为轴旋转后所得圆柱的侧面积都是24π cm2.‎ 第14题图 ‎14．如图所示是一个立方体的展开图，标注了字母A的面是立方体的正面，如果立方体的左面与右面所标注代数式的值相等，且标注的数字相同的不超过2个，求A的取值范围．‎ 解：由题意，得x2＝4x－4，即x2－4x＋4＝0，‎ ‎(x－2)2＝0，∴x＝2，那么x2＝4，4x－4＝4；则4有两个了，‎ ‎∵标注的数字相同的不超过2个，∴A≠4.‎ C　开拓新思路　拓展创新 ‎15．如图所示，MN是圆柱底面的直径，NO是圆柱的高，在圆柱的侧面上，过点M，P有一条绕了四周的路径最短的金属丝，现将圆柱侧面沿NO剪开，所得的侧面展开图可以是：__②__(填序号)．‎ 5‎ 第15题图 ‎16．如图所示，图(a)是过圆柱体木块底面的一条弦AD，沿母线AB剖开后得到的柱体，剖面是矩形ABCD，O为原圆柱体木块底面的圆心．图(b)是该柱体的主视图和俯视图．请你根据图中标注的数据解决以下问题．‎ ‎(1)求弦AD的长度；‎ ‎(2)求这个柱体的侧面积．(结果可保留π和根号)‎ 第16题图 第16题答图 解：(1)过点O作OM⊥AD于点M，连结OD，则△OMD是直角三角形，‎ 易得OD＝36÷2＝18(cm)，‎ OM＝27－18＝9(cm)，‎ ‎∴MD＝9 cm，∴AD＝2MD＝18 (cm)．‎ ‎(2)由(1)易得∠MOD＝60°，‎ 那么∠AOD＝120°，‎ 侧面积之和为18 ×40＋×40‎ ‎＝720 ＋960π(cm2)，‎ ‎∴这个柱体的侧面积为(720 ＋960π)cm2.‎ 5‎