苏州市高新区2012届初中毕业暨升学考试模拟试卷

苏州市高新区2012届初中毕业暨升学考试模拟试卷

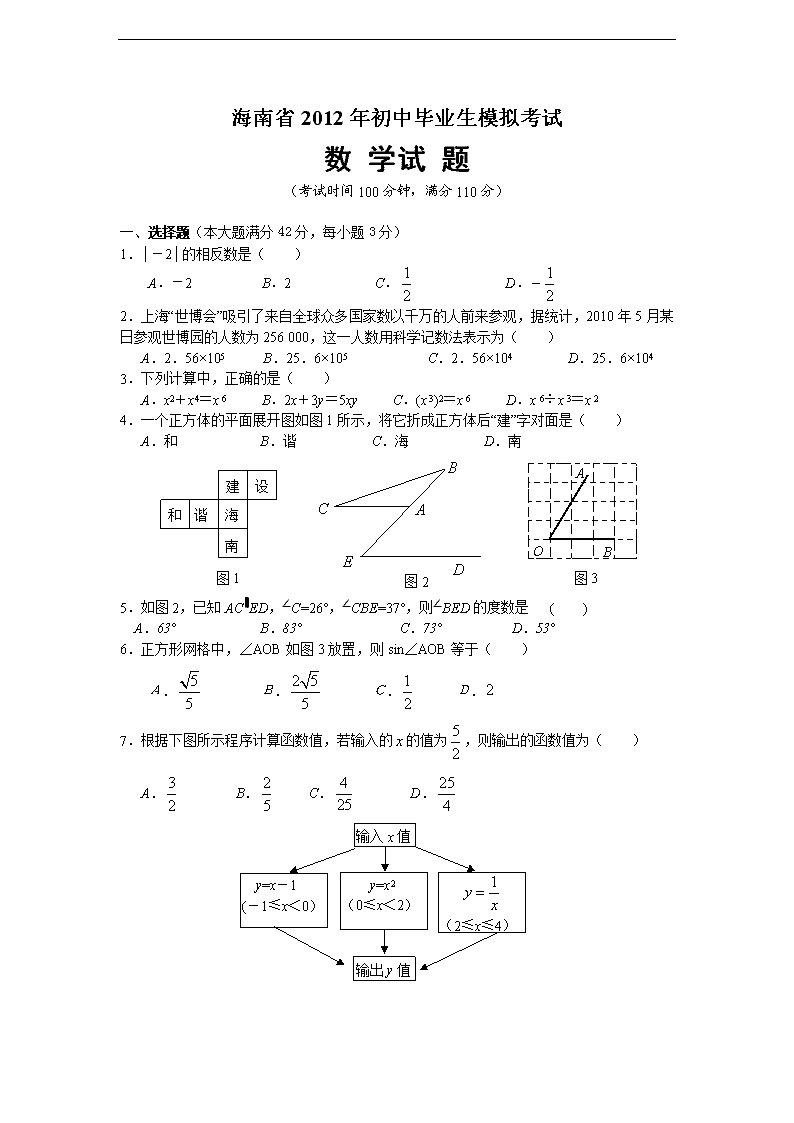
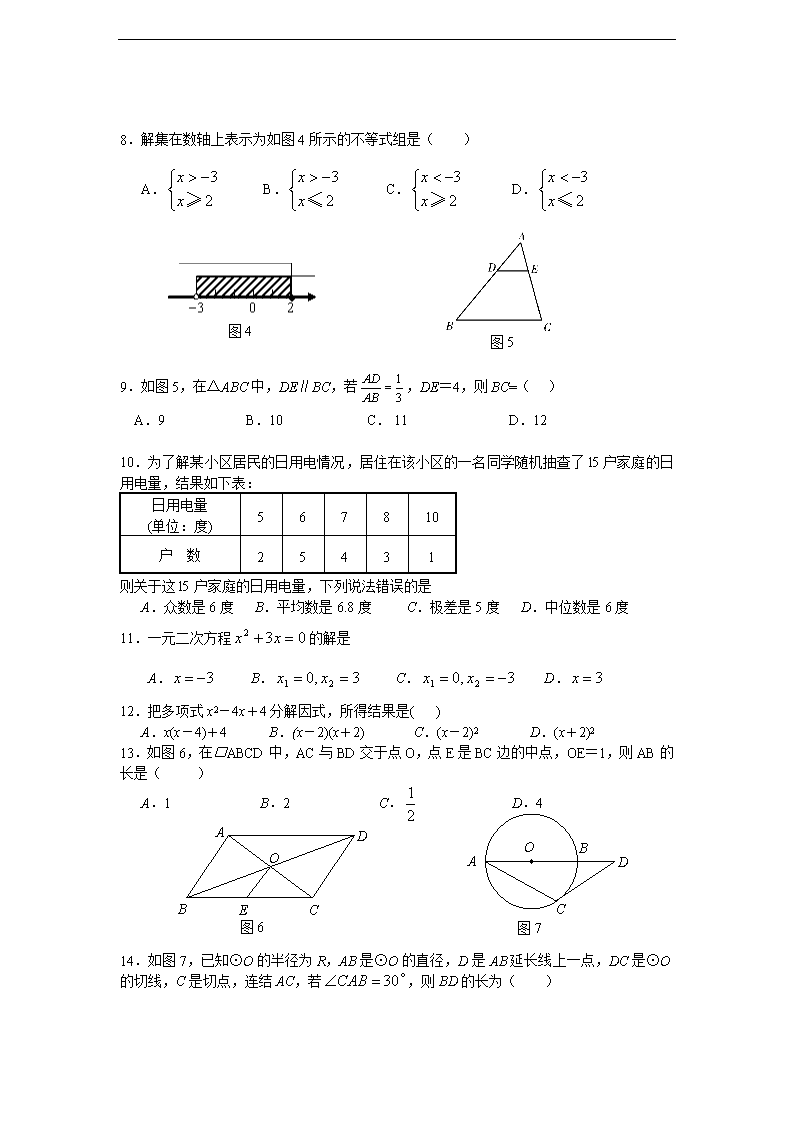
海南省2012年初中毕业生模拟考试 数 学试 题 ‎（考试时间100分钟，满分110分）‎ 一、 选择题（本大题满分42分，每小题3分）‎ ‎1．│－2│的相反数是（ ）‎ A．－2 B．‎2 C． D．‎ ‎2．上海“世博会”吸引了来自全球众多国家数以千万的人前来参观，据统计，2010年5月某日参观世博园的人数为256 000，这一人数用科学记数法表示为（ ）‎ A．2．56×105 B．25．6×‎105 ‎ C．2．56×104 D．25．6×104‎ ‎3．下列计算中，正确的是（ ）‎ A．x2＋x4＝x 6 B．2x＋3y＝5xy C．(x 3)2＝x 6 D．x 6÷x 3＝x 2‎ ‎4．一个正方体的平面展开图如图1所示，将它折成正方体后“建”字对面是（ ）‎ A．和 B．谐 C．海 D．南 A B O 图3‎ A B C D E 图2‎ 建 设 和 谐 海 南 图1‎ ‎5．如图2，已知AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是 ( ) A．63° B．83° C．73° D．53° ‎6．正方形网格中，∠AOB如图3放置，则sin∠AOB等于（ ）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎7．根据下图所示程序计算函数值，若输入的的值为，则输出的函数值为（ ）‎ 输入x值 y=x－1‎ ‎(－1≤x＜0）‎ ‎（2≤x≤4）‎ y=x2‎ ‎（0≤x＜2）‎ 输出y值 A．　　　　B． C．　 　　D．‎ ‎8．解集在数轴上表示为如图4所示的不等式组是（ ）‎ A． B． C． D．‎ 图5‎ 图4‎ ‎9．如图5，在△ABC中，DE∥BC，若，DE＝4，则BC=（    ）‎ ‎ A．9   B．‎10 C． 11         　　 D．12‎ ‎10．为了解某小区居民的日用电情况，居住在该小区的一名同学随机抽查了l5户家庭的日用电量，结果如下表： ‎ 日用电量 ‎(单位：度)‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ 户 数 ‎2‎ ‎5‎ ‎4‎ ‎3‎ l 则关于这l5户家庭的日用电量，下列说法错误的是 A．众数是6度 B．平均数是6.8度 C．极差是5度 D．中位数是6度 ‎11．一元二次方程的解是 A． B． C． D．‎ ‎12．把多项式x2－4x＋4分解因式，所得结果是( )‎ ‎ A．x(x－4)＋4 B．(x－2)(x＋2) C．(x－2)2 D．(x＋2)2‎ ‎13．如图6，在□ABCD中，AC与BD交于点O，点E是BC边的中点，OE＝1，则AB的长是（ ） ‎ O B C D A 图7‎ A O B C D E 图6‎ A．1 B．‎2 ‎C． D．4‎ ‎14．如图7，已知⊙O的半径为R，AB是⊙O的直径，D是AB延长线上一点，DC是⊙O的切线，C是切点，连结AC，若，则BD的长为（ ）‎ A． B． C． D．‎ 一、 选择题（本大题满分12分，每小题3分）‎ ‎15．若点（4，m）在反比例函数(x≠0)的图象上，则m的值是　　　　　　．‎ ‎16．京京玩转盘游戏，当他转动如图8所示的转盘，转盘停止时指针指向2的概率是________;‎ 图10‎ 图9‎ 图8‎ ‎17．如图9，点P在∠AOB的平分线上，若使△AOP≌△BOP，则需添加的一个条件是 ‎ （只写一个即可，不添加辅助线）;‎ ‎18．如图10，⊙O的直径CD＝10，弦AB＝8，AB⊥CD，垂足为M，则DM的长为 ．‎ 二、 选择题（本大题满分56分）‎ ‎19．（满分8分，每小题4分）‎ ‎（1）计算： ;‎ ‎（2）先化简，再求值：，其中.‎ ‎20．（满分8分）某酒店客房部有三人间、双人间客房，收费标准如下表 ：‎ 普通（元/间/天）‎ 豪华（元/间/天）‎ 三人间 ‎150‎ ‎300‎ 双人间 ‎140‎ ‎400‎ 为了吸引游客，实行团体入住五折优惠措施，一个50人的旅游团在优惠期间入住该酒店，住了一些三人普通间和双人普通间客房，若每间客房正好住满，且一天共花去的住宿费为 1510元 ，则该旅游团住了三人普通间和双人普通间客房各多少间？‎ ‎21．（满分8分）某校为了组织一项球类对抗赛，在本校随机调查了若干名学生，对他们每人最喜欢的一项球类运动进行了统计，并绘制成如图11①、②所示的条形和扇形统计图．‎ ‎0‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ ‎10‎ ‎16‎ ‎13‎ 学生人数 篮球 足球 乒乓球 羽毛球 其他 项目 ‎①‎ 足球 ‎20%‎ 篮球 ‎26%‎ 乒乓球 ‎32%‎ 羽毛球 ‎16%‎ 其 他 ‎②‎ 图11‎ 根据统计图中的信息，解答下列问题：‎ ‎（1）学校一共调查了 名学生；并补全条形统计图；‎ ‎（2）若全校有1 500名学生，请你估计该校最喜欢篮球运动的学生约为 人；‎ ‎（3）根据调查结果，请你为学校即将组织的一项球类对抗赛提出一条合理化建议．‎ O x A B ‎1‎ ‎1‎ 图12‎ y ‎22．（满分8分）如图12，在平面直角坐标系中，已知点，轴于A．‎ ‎（1）画出将△OAB绕原点旋转180°后所得的△OA1B1，‎ 并写出点A1、B1的坐标； ‎ ‎（2）将△OAB平移得到△O‎2A2B2，点A的对应 点是A2，点的对应点B2的坐标为，在坐 标系中作出△O‎2A2B2，并写出点O2、A2的坐标；‎ ‎（3）△OA1B1与△O‎2A2B2成中心对称吗？若是，找出 对称中心,并写出对称中心的坐标.‎ ‎23．（满分11分）如图13所示，已知E是边长为1的正方形ABCD对角线BD上一动点，点E从B点向D点运动(与B、D不重合)，过点E作直线GH平行于BC，交AB于点G，交CD于点H，EF⊥AE于点E，交CD(或CD的延长线)于点F.‎ ‎　　(1)如图13（1），求证：△AGE≌△EHF；‎ 图13(1)‎ 图13(2)‎ ‎　　(2)点E在运动的过程中(图13（1）、图13（2）)，四边形AFHG的面积是否发生变化？请说明理由.‎ ‎    ‎ y x 图14‎ A O B C E D ‎24．（满分14分）如图14，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=2，OC=3。‎ ‎（1）求抛物线的解析式；‎ ‎（2）作Rt△OBC的高OD，延长OD与抛物线在 第一象限内交于点E，求点E的坐标；‎ ‎（3）①在x轴上方的抛物线上，是否存在一点P，‎ 使四边形OBEP是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由；‎ ‎②在抛物线的对称轴上，是否存在上点Q，使得 ‎△BEQ的周长最小？若存在，求出点Q的坐标；‎ 若不存在，请说明理由。‎ 海南省2012年初中毕业生模拟考试 数学科试题参考答案 一、 选择题 AACDA BBBDD CCBC 二、 填空题 ‎15．2； 16．； 17．答案不唯一，如：OA=OB等； 18．8‎ 三、 解答题 ‎19．（1）1； （2）‎2a－4＝2×(－1) －4＝－6‎ ‎20．设三人普通客房和双人普通间客房分别住了x、y间，‎ 根据题意，得 ‎3x＋2y＝50‎ ‎150×0．5x＋140×0．5y＝1510‎ x＝8‎ 解得 ‎ y＝13‎ 答：三人普通客房和双人普通间客房分别住了8、13间。‎ ‎21．（1）50，图略； （2）390； （3）略。‎ ‎ 22．（1）图略，A1（－4，0） B1（－4，－2）；‎ ‎（2）图略，O2（－2，－4） A2（2，－4）；‎ ‎（3）图略，对称中心的坐标为（－1，－2）。‎ ‎23． (1)∵四边形ABCD是正方形，BD是对角线，且GH∥BC，‎ ‎　　∴四边形AGHD和四边形GHCB都是矩形，‎ ‎　　△GEB和△HDE都是等腰直角三角形.‎ ‎∴∠AGE=∠EHF=90°， GH=BC=AB ，EG =BG ‎∴GH－EG= AB－BG 即EH=AG ‎　　∴∠EFH+∠FEH=90°‎ ‎　　又∵EF⊥AE，∴∠AEG+∠FEH=90°.‎ ‎　　∴∠EFH=∠AEG ‎∴△AGE≌△EHF ‎　　(2)四边形AFHG的面积没有发生变化 ‎　　(i)当点E运动到BD的中点时，‎ 四边形AFHG是矩形，S四边形AFHG=‎ ‎(ii)当点E不在BD的中点时，点E在运动(与点B、D不重合)的过程中，四边形AFHG是直角梯形.‎ ‎　　由(1)知，△AGE≌△EHF ‎　　同理，图13（2），△AGE≌△EHF ‎　　∴FH =EG =BG.‎ ‎∴FH+AG=BG＋AG=AB=1‎ 这时，S四边形AFHG=（FH＋AG）·GH=‎ 综合(i)、(ii)可知四边形AFNM的面积没有发生改变，都是。‎ ‎24．（1）∵OA＝2，∴点A的坐标为（－2，0）.‎ ‎∵OC＝3，∴点C的坐标为（0，3）.‎ ‎∵把（－2，0），（0，3）代入，得 ‎0＝－2－2b＋c b＝‎ ‎ 解得 ‎3＝c c＝3‎ ‎∴抛物线解析式为。‎ ‎（2）把y＝0代入，‎ 解得x1＝－2, x2＝3‎ ‎∴点B的坐标为（3，0），∴OB＝OC＝3‎ ‎∵OD⊥BC，∴OD平分∠BOC ‎∴OE所在的直线为y＝x x 图14－1‎ A O B C E D P y＝x x1＝2， x2＝－3‎ 解方程组 得 y ‎ y1＝2， y2＝－3‎ ‎∵点E在第一象限内，∴点E的坐标为（2，2）。‎ ‎（3）存在，如图14－1，过点E作x轴的平行线与抛物线 交于另一点P，连接BE、PO，‎ 把y＝2代入，‎ 解得x1＝－1, x2＝2‎ ‎∴点P的坐标为（－1，2）‎ ‎∵PE∥OB，且PE＝OB＝3‎ x 图14－2‎ A O B C E D Q ‎∴四边形OBEP是平行四边形 ‎∴在x轴上方的抛物线上，存在一点P（－1，2），‎ 使得四边形OBEP是平行四边形。‎ ‎（4）存在，如图14－2，设Q是抛物线对称轴上的 一点，连接QA、QB、QE、BE ‎∵QA＝QB，‎ ‎∴△BEQ的周长等于BE＋QA＋QE 又∵BE的长是定值 ‎∴A、Q、E在同一直线上时，△BEQ的周长最小，‎ 由A（－2，0）、E（2，2）可得直线AE的解析式为 ‎∵抛物线的对称轴是x＝‎ ‎∴点Q的坐标为（，）‎ 所以，在抛物线的对称轴上，存在点Q（，），使得△BEQ的周长最小。‎