人教版九年级数学上册同步测试题课件（8）

人教版九年级数学上册同步测试题课件（8）

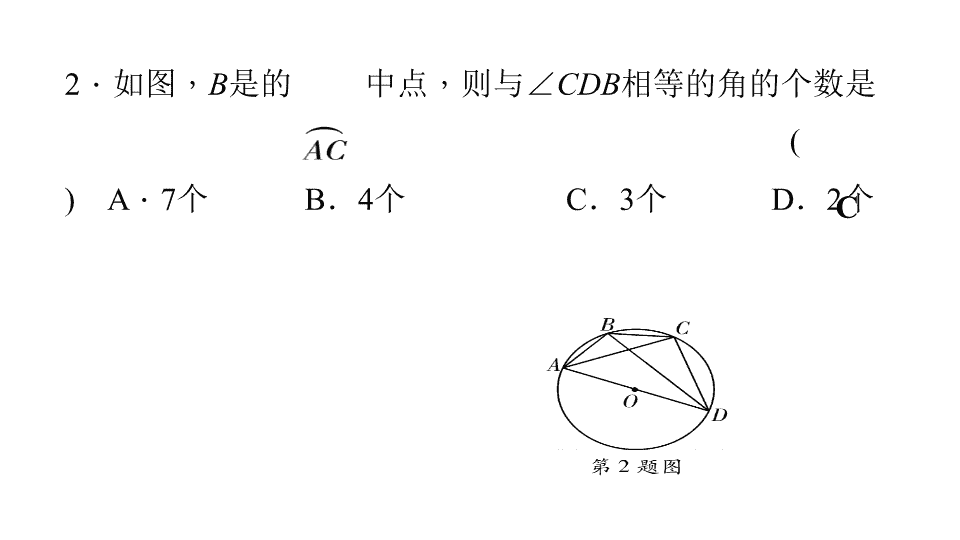
周周测 ( 八 )(24.1) 时间： 45 分钟　满分： 100 分　姓名： ________ 一、选择题 ( 每小题 3 分 ， 共 24 分 ) 1. 下 列说法： ① 直径是弦； ② 弦是半径； ③ 半圆是弧； ④ 弧是半圆，其中正确 的有 ( 　 　 ) A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个 B C 2 ． 如图 ， B 是的 中点 ， 则与 ∠ CDB 相等的角的个数是 ( 　 　 ) A ． 7 个 B ． 4 个 C ． 3 个 D ． 2 个 D 　 3 ． ( 广州中考 ) 如图 ， 在 ⊙ O 中 ， AB 是直径 ， CD 是弦 ， AB ⊥ CD ， 垂足为 E ， 连接 CO ， AD ， ∠ BAD ＝ 20° ， 则下列说法中正确的是 ( 　 　 ) C 4 ． ( 广东中考 ) 如图 ， 四边形 ABCD 内接于 ⊙ O ， DA ＝ DC ， ∠ CBE ＝ 50° ， 则 ∠ DAC 的大小为 ( 　　 ) A ． 130 ° B ． 100° C ． 65° D ． 50° B 5 ． 如图 ， 小华同 学设计了一个圆直径的测量器 ， 标有刻度的尺子 OA ， OB 在 O 点钉在一起 ， 并使它们保持垂直 ， 在测量直径时 ， 把 O 点靠在圆周上 ， 读得刻度 OE ＝ 8 个单位 ， OF ＝ 6 个单位 ， 则圆的直径为 （ ） ( 　 　 ) A 7 ． 已知 ⊙ O 是 △ ABC 的外接圆 ， ∠ B ＝ 60° ， ⊙ O 的 半径为 4 ， 则 AC 的长等于 ( 　 　 ) A ． 4 B ． 6 C ． 2 D ． 8 B 8 ． ★ 如图 ， 在 ⊙ O 中 ， ∠ AOB 的度数为 m ， C 是 上一点 ， D ， E 是 上不同的两点 ( 不与 A ， B 两点重合 ) ， 则 ∠ D ＋ ∠ E 的度数为 ( 　 　 ) 二、填空题 ( 每小题 4 分 ， 共 24 分 ) 9 ． 如图 ， AB ， CD 是 ⊙ O 的直径 ， 弦 DE ∥ AB ， 则 AC 与 AE 的大小关系是 10 ． ( 长沙中考 ) 如图 ， AB 为 ⊙ O 的直径 ， 弦 CD ⊥ AB 于点 E ， 已知 CD ＝ 6 ， EB ＝ 1 ， 则 ⊙ O 的半径为 11 ． 如图 ， 点 A ， B ， C 在 ⊙ O 上 ， CO 的延长线交 AB 于点 D ， ∠ A ＝ 50° ， ∠ B ＝ 30° ， 则 ∠ ADC 的度数为 12 ． 在圆内接四边形 ABCD 中 ， 若 ∠ A ， ∠ B ， ∠ C 的度数之比为 4 ∶ 3 ∶ 5 ， 则 ∠ D 的度数是 . 13 ． ( 常州中考 ) 如图 ， 四边形 ABCD 内接于 ⊙ O ， AB 为 ⊙ O 的直径 ， 点 C 为弧 BD 的中点 ， 若 ∠ DAB ＝ 40° ， 则 ∠ ABC ＝ . 14 ． ★ 如图 ， 将 ⊙ O 沿弦 AB 折叠 ， 点 C 在 上点 D 在 上 ， 若 ∠ ACB ＝ 70° ， 则 ∠ ADB ＝ . 三、解答题 ( 共 52 分 ) 15 ． (10 分 ) 如图 ， A ， B ， C ， D 四点在 ⊙ O 上 ， 且 AB ＝ CD ， 求证： AC ＝ BD . 证明： ∵ 四边形 ABCD 为圆内接四边形 ， ∴∠ BCD ＋ ∠ BAD ＝ 180° ， 又 ∠ BCD ＋ ∠ MCD ＝ 180° ， ∴∠ BAD ＝ ∠ MCD. ∵ CD 为 ∠ BCA 的外角的平分线 ， ∴∠ MCD ＝ ∠ DCA ， 又 ∠ DBA ＝ ∠ DCA ， ∴∠ BAD ＝ ∠ DBA ， ∴ DB ＝ DA ， ∴△ ABD 为等腰三角形． 16 ． (10 分 ) 如图 ， 在圆内接四边形 ABCD 中 ， CD 为 ∠ BCA 的外角的平分线 ， 求证： △ ABD 为等腰三角形． 17 ． (10 分 ) 如图所示 ， 某窗户是由矩形和弓形组成 ， 已知弓形的跨度 AB ＝ 3 m ， 弓形的高 EF ＝ 1 m ， 现计划安装玻璃 ， 请帮工程师求出 所在圆 O 的半径 r . 解：由题意知 OA ＝ OE ＝ r. ∵ EF ＝ 1 ， ∴ OF ＝ r － 1. ∵ OE ⊥ AB ， ∴ AF ＝ AB ＝ × 3 ＝ 1.5. 在 Rt △ OAF 中 ， OF 2 ＋ AF 2 ＝ OA 2 ， 即 ( r － 1 ) 2 ＋ 1.5 2 ＝ r 2 ， 解得 r ＝ . 即圆 O 的半径为 米． 18 ． (10 分 ) 如图所示 ， 已知 ⊙ O ′ 与平面直角坐标系交于 A ， O ， B 三点 ， 点 C 在 ⊙ O ′ 上 ， 点 A 的坐标为 (0 ， 2 ) ， ∠ COB ＝ 45° ， ∠ OBC ＝ 75° ， 求 ⊙ O ′ 的直径． 解：连接 AB. ∵ AB 是 ⊙ O′ 的弦 ， ∠ AOB ＝ 90° ， ∴ AB 为 ⊙ O′ 的直径． ∵∠ C ＝ 180° － 75° － 45° ＝ 60° ， ∴∠ OAB ＝ ∠ C ＝ 60° ， 在 Rt △ AOB 中 ， OA ＝ 2 ， ∴ AB ＝ 4. 即 ⊙ O′ 的直径为 4. 　 19 ． (12 分 ) 已知 ⊙ O 的直径为 10 ， 点 A ， 点 B ， 点 C 在 ⊙ O 上 ， ∠ CAB 的平分线交 ⊙ O 于点 D . (1) 如图 ① ， 若 BC 为 ⊙ O 的直径 ， AB ＝ 6 ， 求 AC ， BD ， CD 的长； (2) 如图 ② ， 若 ∠ CAB ＝ 60° ， 求 BD 的长． 解： ( 1 ) ∵CB 是直径 ， ∴∠ CDB ＝ ∠CAB ＝ 90°. ∵ AB ＝ 6 ， CB ＝ 10 ， ∴ AC ＝ 8 ， ∵ AD 平分 ∠CAB. ∴ ， ∴ CD ＝ BD ， ∴ 在 Rt △ CDB 中 ， CD ＝ DB ＝ 5 . ( 2 ) 连接 OB ， OD ， ∵∠ CAB ＝ 60° ， ∴∠ DAB ＝ 30° ， ∴∠ BOD ＝ 60° ， 又 ∵ OB ＝ OD ， ∴△ OBD 是等边三角形 ， ∴ BD ＝ 5.