北师大版八年级上册第4章：一次函数与菱形（含解析）

北师大版八年级上册第4章：一次函数与菱形（含解析）

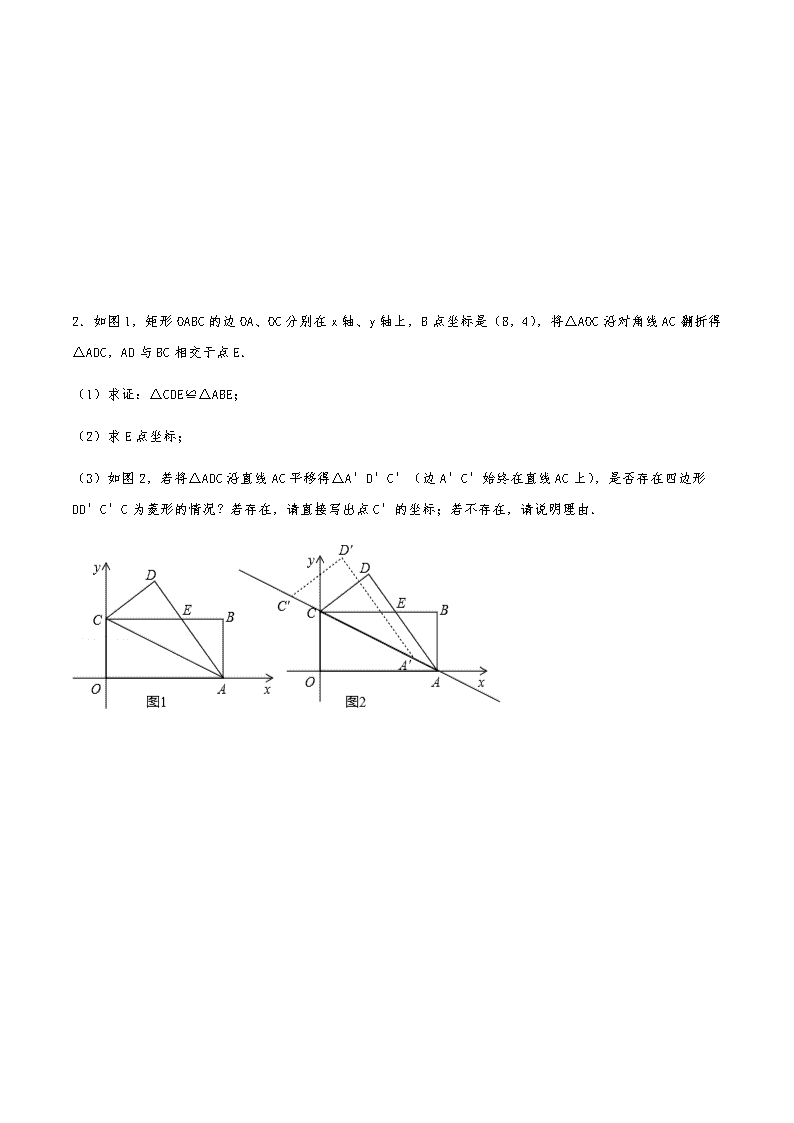
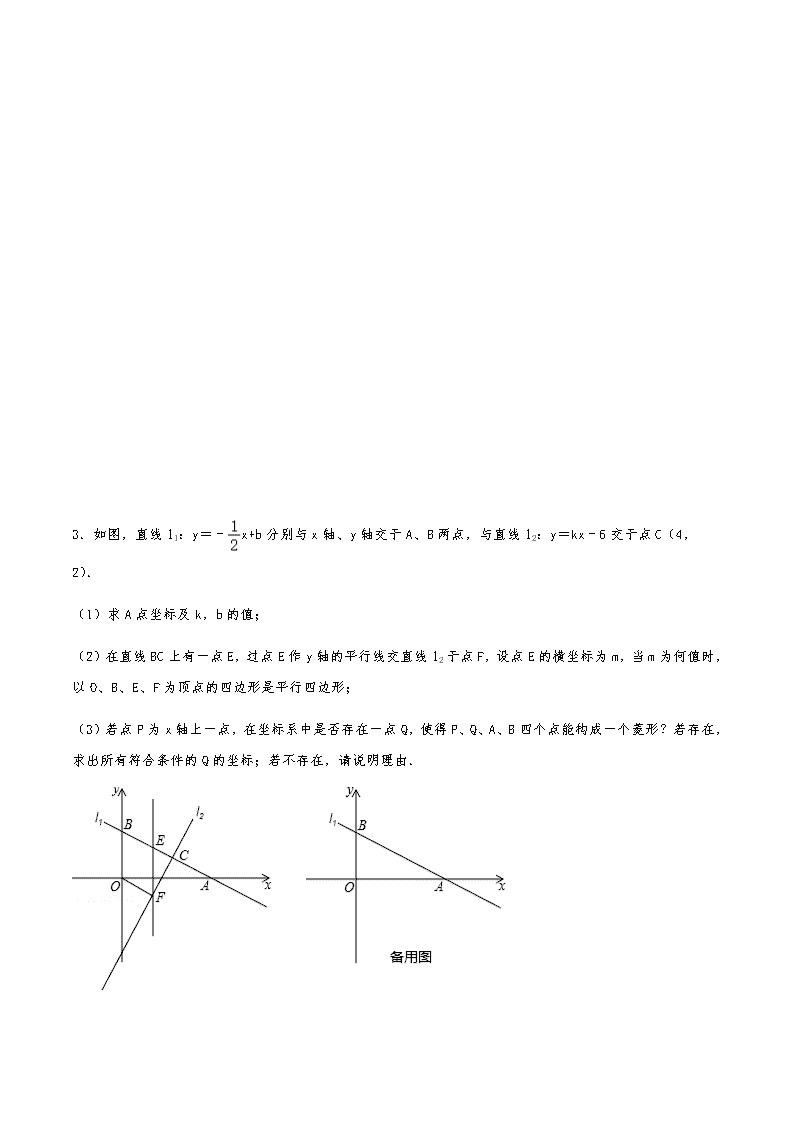
一次函数压轴题之菱形1．如图，直线l1：y＝﹣x+b分别与x轴、y轴交于A、B两点，与直线l2：y＝kx﹣6交于点C（4，2）（1）求直线l1和直线l2的解析式；（2）点E是射线BC上一动点，其横坐标为m，过点E作EF∥y轴，交直线l2于点F，若以O、B、E、F为顶点的四边形是平行四边形，求m值；（3）若点P为x轴上一点，则在平面直角坐标系中是否存在一点Q，使得以P、Q、A、B为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由． 2．如图1，矩形OABC的边OA、OC分别在x轴、y轴上，B点坐标是（8，4），将△AOC沿对角线AC翻折得△ADC，AD与BC相交于点E．（1）求证：△CDE≌△ABE；（2）求E点坐标；（3）如图2，若将△ADC沿直线AC平移得△A′D′C′（边A′C′始终在直线AC上），是否存在四边形DD′C′C为菱形的情况？若存在，请直接写出点C′的坐标；若不存在，请说明理由． 3．如图，直线l1：y＝﹣x+b分别与x轴、y轴交于A、B两点，与直线l2：y＝kx﹣6交于点C（4，2）．（1）求A点坐标及k，b的值；（2）在直线BC上有一点E，过点E作y轴的平行线交直线l2于点F，设点E的横坐标为m，当m为何值时，以O、B、E、F为顶点的四边形是平行四边形；（3）若点P为x轴上一点，在坐标系中是否存在一点Q，使得P、Q、A、B四个点能构成一个菱形？若存在，求出所有符合条件的Q的坐标；若不存在，请说明理由． 4．在平面直角坐标系中，BC∥OA，BC＝3，OA＝6，AB＝3（1）直接写出点B的坐标；（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2BE，直线DE交x轴于点F，求直线DE的解析式；（3）在（2）的条件下，点M是直线DE上的一点，在x轴上方是否存在另一个点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由． 5．如图，在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+b与坐标轴交于C，D两点，直线AB与坐标轴交于A，B两点，线段OA，OC的长是方程x2﹣3x+2＝0的两个根（OA＞OC）．（1）求点A，C的坐标；（2）直线AB与直线CD交于点E，若点E是线段AB的中点，求直线AB的解析式；（3）在（2）的条件下，点M在直线CD上，坐标平面内是否存在点N，使以点B，E，M，N为顶点的四边形是菱形？若存在，请直接写出满足条件的点N的坐标；若不存在，请说明理由． 6．在平面直角坐标系中，直线y＝﹣x+b分别与x轴、y轴交于点A、B，且点A坐标为（8，0），点C为AB中点．（1）请直接写出点B坐标（　　，　　）．（2）点M为x轴上的一个动点，过点M作x轴的垂线，分别与直线AB、直线OC交于点P、Q，设点M的横坐标为m，线段PQ的长度为d，求d与m的函数关系式，并直接写出自变量m的取值范围．（3）在（2）条件下，当点M在线段OA（点M不与O、A重合）上运动时，在坐标系内是否存在一点N，使得以O、B、P、N为顶点的四边形为菱形？若存在，求出N点的坐标若不存在，请说明理由． 7．如图，平面直角坐标系中，矩形OABC的对角线AC＝12，∠ACO＝30°，（1）求B、C两点的坐标；（2）把矩形沿直线DE对折使点C落在点A处，DE与AC相交于点F，求直线DE的解析式；（3）若点M在直线DE上，平面内是否存在点N，使以O、F、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由． 8．如图，已知点A（﹣12，0），B（3，0），点C在y轴的正半轴上，且∠ACB＝90°．（1）求点C的坐标；（2）求Rt△ACB的角平分线CD所在直线l的解析式； （3）在l上求出满足S△PBC＝S△ABC的点P的坐标；（4）已知点M在l上，在平面内是否存在点N，使以O、C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在．请说明理由． 9．如图，在平面直角坐标系中，▱OABC的顶点A在y轴的正半轴上，顶点B在x轴的正半轴上，对角线AC、OB交于点D，且OA、OB的长是方程x2﹣12x+32＝0的两根（OA＜OB）．（1）求直线AC的函数解析式；（2）若点P从A点出发，以每秒1个单位的速度沿射线AC运动，连接OP．设△OPD的面积为S，点P的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围；（3）若点M是直线AC上一点，则在平面上是否存在点N，使以A、B、M、N为顶点四边形为菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由． 10．如图，在平面直角坐标系中，直角梯形OABC的边OC、OA分别与x轴、y轴重合，AB∥OC，∠AOC＝90°，∠BCO＝45°，BC＝12，点C的坐标为（﹣18，0）．（1）求点B的坐标；（2）若直线DE交梯形对角线BO于点D，交y正半轴于点E，且OE＝4，OD＝2BD，求直线DE的解析式；（3）若点P是（2）中直线DE上的一个动点，在坐标平面内是否存在点Q，使以O、E、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由． 11．如图，在Rt△OAB中，∠A＝90°，∠ABO＝30°，OB＝，边AB的垂直平分线CD分别与AB、x轴、y轴交于点C、G、D．（1）求点G的坐标；（2）求直线CD的解析式；（3）在直线CD上和平面内是否分别存在点Q、P，使得以O、D、P、Q为顶点的四边形是菱形？若存在，求出点Q的坐标；若不存在，请说明理由． 12．已知直线y＝x+4与x轴、y轴分别交于A、B两点，∠ABC＝60°，BC与x轴交于点C．（1）试确定直线BC的解析式．（2）若动点P从A点出发沿AC向点C运动（不与A、C重合），同时动点Q从C点出发沿CBA向点A运动（不与C、A重合），动点P的运动速度是每秒1个单位长度，动点Q的运动速度是每秒2个单位长度．设△APQ的面积为S，P点的运动时间为t秒，求S与t的函数关系式，并写出自变量的取值范围．（3）在（2）的条件下，当△APQ的面积最大时，y轴上有一点M，平面内是否存在一点N，使以A、Q、M、N为顶点的四边形为菱形？若存在，请直接写出N点的坐标；若不存在，请说明理由． 13．如图，在平面直角坐标系中，已知点A为第二象限内一点，过点A作x轴垂线交x轴于点B，点C为x轴正半轴上一点，且OB、OC的长分别为方程x2﹣4x+3＝0的两根（OB＜OC）．（1）求B、C两点的坐标；（2）作直线AC，过点C作射线CE⊥AC于C，在射线CE上有一点M（5，2），求直线AC的解析式；（3）在（2）的条件下，坐标平面内是否存在点Q和点P（点P在直线AC上），使以O、C、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点坐标；若不存在，请说明理由． 14．如图1，直线y＝﹣x+6与y轴交于点A，与x轴交于点D，直线AB交x轴于点B，△AOB沿直线AB折叠，点O恰好落在直线AD上的点C处．（1）求OB的长；（2）如图2，F，G是直线AB上的两点，若△DFG是以FG为斜边的等腰直角三角形，求点F的坐标；（3）如图3，点P是直线AB上一点，点Q是直线AD上一点，且P，Q均在第四象限，点E是x轴上一点，若四边形PQDE为菱形，求点E的坐标． 1．【解答】解：（1）将点C的坐标代入l1、l2表达式得：2＝﹣4+b，2＝4k﹣6，解得：b＝4，k＝2，故直线l1和直线l2的解析式分别为：y＝﹣x+4，y＝2x﹣6， 则点A、B的坐标分别为（8，0）、（0，4）；（2）设点E（m，﹣m+4），点F（m，2m﹣6），当以O、B、E、F为顶点的四边形是平行四边形时，则EF＝OB，即|﹣m+4﹣2m+6|＝4，解得：m＝或；（3）①当AB是菱形的一条边时，则AP＝AB＝＝4，则点P的坐标为（8+4，0）或（8﹣4，0）或（﹣8，0），则点Q（4，4）或（﹣4，4）或（0，﹣4）；②当AB是菱形的对角线时，设点P（m，0），点Q（s，t），由中点公式得：8＝m+s，4＝t…①，由菱形性质知：PA＝PB得：（m﹣8）2＝m2+16…②，联立①②并解得：t＝4，s＝5，故点Q（5，4），综上，点Q（4，4）或（﹣4，4）或（5，4）或（0，﹣4）．2．【解答】解：（1）证明：∵四边形OABC为矩形，∴AB＝OC，∠B＝∠AOC＝90°，∴CD＝OC＝AB，∠D＝∠AOC＝∠B，又∠CED＝∠ABE，∴△CDE≌△ABE（AAS），∴CE＝AE； （2）∵B（8，4），即AB＝4，BC＝8．∴设CE＝AE＝n，则BE＝8﹣n，可得（8﹣n）2+42＝n2，解得：n＝5，∴E（5，4）；（3）设点C在水平方向上向左移动m个单位，则在垂直方向上向上移动了个单位，则点C′坐标为（﹣m，4m），则∵四边形DD′C′C为菱形，∴CC′2＝（﹣m）2+（m）2＝m2＝CD2＝16，解得：m＝±，故点C′的坐标为（，4+）或（，4﹣）．3．【解答】解：（1）将C（4，2）代入y＝kx﹣6，y＝﹣x+b得：2＝4k﹣6，2＝﹣×4+b，解得：k＝2，b＝4∴直线l1：y＝﹣x+4，直线l2：y＝2x﹣6在y＝﹣x+4中，令x＝0，得y＝4，∴B（0，4）令y＝0，得0＝﹣x+4，解得：x＝8，∴A（8，0）；（2）设E（m，﹣m+4），则F（m，2m﹣6），如图1，当0≤m≤4时，EF＝10，∵四边形OBEF是平行四边形 ∴OB＝EF即4＝10，解得：m＝，如图2，当m＞4时，∵四边形OBFE是平行四边形∴OB＝FE，即4＝m﹣10，解得：m＝，∴m＝或m＝；（3）存在．如图3，①当以AB为边时，∵点A（8，0），B（0，4）∴AB＝＝＝4，∵以P、Q、A、B为顶点的四边形是菱形∴AP＝AB＝4，∴P（8﹣4，0）或P（8+4，0），∴Q（﹣4，4）或（4，4），当Q与B关于原点对称时，Q（0，﹣4）也存在满足条件的菱形，②当以AB为对角线时，设对角线的交点为M，则M（4，2），因此设AP＝BP＝x，则OP＝8﹣x，∴在Rt△BOP中，42+（8﹣x）2＝x2，解得：x＝5，∴P（3，0），则Q（5，4）， 综上所述，符合条件的Q的坐标为：Q（﹣4，4）或（4，4）或（5，4）或（0，﹣4）．4．【解答】解：（1）如图1，过B作BG⊥OA于点G， ∵BC＝3，OA＝6，∴AG＝OA﹣OG＝OA﹣BC＝6﹣3＝3，在Rt△ABG中，由勾股定理可得AB2＝AG2+BG2，即（3）2＝32+BG2，解得BG＝6，∴OC＝6，∴B（3，6）；（2）由OD＝5可知D（0，5），∵B（3，6），OE＝2BE，∴E（2，4），设直线DE的解析式是y＝kx+b把D（0，5）E（2，4）代入得，∴直线DE的解析式是y＝﹣x+5；（3）当OD为菱形的边时，则MN＝OD＝5，且MN∥OD，∵M在直线DE上，∴设M（t，﹣t+5），①当点N在点M上方时，如图2，则有OM＝MN， ∵OM2＝t2+（﹣t+5）2，∴t2+（﹣t+5）2＝52，解得t＝0或t＝4，当t＝0时，M与D重合，舍去，∴M（4，3），∴N（4，8）；②当点N在点M下方时，如图3，则有MD＝OD＝5，∴t2+（﹣t+5﹣5）2＝52，解得t＝2或t＝﹣2，当t＝2时，N点在x轴下方，不符合题意，舍去，∴M（﹣2，+5），∴N（﹣2，）；当OD为对角线时，则MN垂直平分OD， ∴点M在直线y＝2.5上，在y＝﹣x+5中，令y＝2.5可得x＝5，∴M（5，2.5），∵M、N关于y轴对称，∴N（﹣5，2.5），综上可知存在满足条件的点N，其坐标为（4，8）或（﹣5，2.5）或（﹣2，）．5．【解答】解：（1）x2﹣3x+2＝（x﹣1）（x﹣2）＝0，∴x1＝1，x2＝2，∵OA＞OC，∴OA＝2，OC＝1，∴A（﹣2，0），C（1，0）．（2）将C（1，0）代入y＝﹣x+b中，得：0＝﹣1+b，解得：b＝1，∴直线CD的解析式为y＝﹣x+1．∵点E为线段AB的中点，A（﹣2，0），B的横坐标为0，∴点E的横坐标为﹣1．∵点E为直线CD上一点，∴E（﹣1，2）．设直线AB的解析式为y＝kx+b，则有，解得， ∴直线AB的解析式为y＝2x+4．（3）假设存在，设点M的坐标为（m，﹣m+1），以点B，E，M，N为顶点的四边形是菱形分两种情况（如图所示）：①以线段BE为边时，∵E（﹣1，2），A（﹣2，0），E为线段AB的中点，∴B（0，4），∴BE＝AB＝＝．∵四边形BEMN为菱形，∴EM＝BE或BE＝BM．当EM＝BE时，有EM＝＝BE＝，解得：m1＝，m2＝，∴M（，2+）或（，2﹣），∵B（0，4），E（﹣1，2），∴N（﹣，4+）或（，4﹣）；当BE＝BM时，有BM＝＝BE＝，解得：m3＝﹣1（舍去），m4＝﹣2，∴M（﹣2，3），∵B（0，4），E（﹣1，2），∴N（﹣3，1）；②以线段BE为对角线时，MB＝ME， ∴＝，解得：m3＝﹣，∴M（﹣，），∵B（0，4），E（﹣1，2），∴N（0﹣1+，4+2﹣），即（，）．综上可得：坐标平面内存在点N，使以点B，E，M，N为顶点的四边形是菱形，点N的坐标为（﹣，4+）或（，4﹣）或（﹣3，1）或（，）；6．【解答】解：（1）∵直线y＝﹣x+b过点A（8，0），∴0＝﹣6+b，解得：b＝6，∴直线AB的解析式为y＝﹣x+6．令y＝﹣x+6中x＝0，则y＝6，∴点B的坐标为（0，6）．故答案是：（0，6）． （2）依照题意画出图形，如图3所示．∵A（8，0），B（0，6），且点C为AB的中点，∴C（4，3）．设直线OC的解析式为y＝kx（k≠0），则有3＝4k，解得：k＝，∴直线OC的解析式为y＝x．∵点P在直线AB上，点Q在直线OC上，点P的横坐标为m，PQ⊥x轴，∴P（m，﹣m+6），Q（m，m）．当m＜4时，d＝﹣m+6﹣m＝﹣m+6；当m＞4时，d＝m﹣（﹣m+6）＝m﹣6．故d与m的函数解析式为d＝；（3）假设存在，设点P的坐标为（n，﹣n+6）（0＜n＜8）．∵点P在第一象限，∴以O，B，P，N为顶点的四边形为菱形有两种情况：①以BP为对角线时，如图4所示．∵四边形OPNB为菱形，B（0，6），∴OP＝OB＝6＝，解得：n＝或n＝0（舍去）， ∴点P（，），∴点N（+0﹣0，6+﹣0），即（，）②以OP为对角线时，如图5所示．PN∥OB，PN＝ON＝OB＝6．∴MN＝PN﹣PM＝m．在直角△ONM中，OM2+MN2＝ON2，即m2+（m）2＝62．解得m＝（舍去负值）．此时N（，﹣）；③当OB为对角线时，N（﹣4，3）．综上得：当点P在线段AB（点M不与A，B重合）上运动时，在坐标系第一象限内存在一点N，使得以O，B，P，N为顶点的四边形为菱形，N点坐标为（，）或（，﹣）或N（﹣4，3）． 7．【解答】解：（1）在直角△OAC中，tan∠ACO＝＝，∴设OA＝x，则OC＝3x，根据勾股定理得：（3x）2+（x）2＝AC2，即9x2+3x2＝144，解得：x＝2．故C的坐标是：（6，0），B的坐标是（6，6）；（2）直线AC的斜率是：﹣＝﹣，则直线DE的斜率是：．F是AC的中点，则F的坐标是（3，3），设直线DE的解析式是y＝x+b，则9+b＝3，解得：b＝﹣6，则直线DE的解析式是：y＝x﹣6；（3）OF＝AC＝6，∵直线DE的斜率是：．∴DE与x轴夹角是60°，当FM是菱形的边时（如图1），ON∥FM， 则∠NOC＝60°或120°．当∠NOC＝60°时，过N作NG⊥y轴，则NG＝ON•sin30°＝6×＝3，OG＝ON•cos30°＝6×＝3，则N的坐标是（3，3）；当∠NOC＝120°时，与当∠NOC＝60°时关于原点对称，则坐标是（﹣3，﹣3）；当OF是对角线时（如图2），MN关于OF对称．∵F的坐标是（3，3），∴∠FOD＝∠NOF＝30°，在直角△ONH中，OH＝OF＝3，ON＝＝＝2．作NL⊥y轴于点L．在直角△ONL中，∠NOL＝30°，则NL＝ON＝，OL＝ON•cos30°＝2×＝3．故N的坐标是（，3）．当DE与y轴的交点时M，这个时候N在第四象限，此时点的坐标为：（3，﹣3）．则N的坐标是：（3，﹣3）或（3，3）或（﹣3，﹣3）或（，3）． 8．【解答】解：（1）由△AOC∽△COB，可得OC2＝OA×OB＝36，∴OC＝6又∵点C在y轴的正半轴上，∴点C的坐标是（0，6）；（2）过点D作DE⊥BC于点E．设DB的长为m．在Rt△DEB中，DE＝DB•sinB＝m•＝m，BE＝DB•cosB＝m在Rt△DEC中，∠DCE＝45°，于是CE＝DE＝m由CE+BE＝BC，即m+m＝3，解得m＝5又由OA＞OB，知点D在线段OA上，OB＝3，所以OD＝2，故点D（﹣2，0）；设直线l的解析式为：y＝kx+b，把C（0，6）和D（﹣2，0）代入y＝kx+b中，得，解得．故直线l的解析式为：y＝3x+6；（3）①取AB的中点F（﹣4.5，0），过点F作BC的平行线交直线l于点P1，连接CF．易知S△P1BC＝S△FBC＝S△ACB，∴点P1为符合题意的点． 直线P1F可由直线BC向左平移BF个单位得到（即向左平移7.5个单位）而直线BC的解析式为y＝﹣2x+6，即直线P1F的解的式为y＝﹣2（x+7.5）+6即y＝﹣2x﹣9，由得点P1（﹣3，﹣3）②在直线l上取点P2使CP2＝CP1，此时有S△P2BC＝S△P1BC＝S△ACB，∴点符P2合题意．由CP2＝CP1，过P1点作P1M⊥MO，垂足为M，过P2点作P2N⊥NO，垂足为N，由CP2＝CP1易知MC＝NC，可得点P2的坐标为（3，15），∴点P（﹣3，﹣3）或P（3，15）可使S△PBC＝S△ABC；（4）①当OC是菱形的对角线时（如图1所示），OC的中点的坐标是（0，3），则把y＝3代入l的解析式得：3x+6＝3，解得：x＝﹣1．则M的坐标是（﹣1，3），N的坐标是（1，3）；②当CM为菱形的对角线时（如图2所示），此时M2O＝CO，设M2的坐标为（m，3m+6），所以m2+（3m+6）2＝62，解得m＝﹣，则M2（﹣，﹣），又M2N2∥OC且M2N2＝OC，易知N2（﹣，）； ③当OC和CM均为菱形的边时，此时M3N3＝CO，设M3的坐标为（m，3m+6），所以m2+（3m+6﹣6）2＝62，解得m＝﹣或﹣，易知N点的坐标为（，）或（﹣，﹣）．综上所述，N的坐标是（1，3）或（﹣，）或（，）或（﹣，﹣）．9．【解答】解：（1）∵OA、OB的长x2﹣12x+32＝0的两根，OA＜OB，∴OA＝4，OB＝8，点A坐标为（0，4），点B坐标为（8，0），又∵四边形ABCD是平行四边形，∴可得点C的横坐标等于点B的横坐标，点C的纵坐标等于点A的纵坐标的相反数，故点C的坐标为（8，﹣4），设直线AC的解析式为：y＝kx+b，则， 解得：，故直线AC的解析式为：y＝﹣x+4；（2）由（1）可得OB＝8，根据平行四边形的性质可得点D坐标为（4，0），即OA＝OD，∠OAD＝∠ODA＝45°，AD＝4，①当点P在线段AD上时，此时t＜4；过点P作PE⊥OA，PF⊥OB，则可得AP＝t，在RT△AEP中，EP＝t，即点P的横坐标为t，∵点P在直线AC上，∴点P的纵坐标为：﹣t+4，此时S△OPD＝OD×P纵坐标＝8﹣t（t＜4）；②当点P在射线DC上时，此时t＞4 PD＝AP﹣AD＝t﹣4，在RT△PDM中，PM＝DPcos∠DPM＝DP×＝t﹣4，此时S△OPD＝OD×P纵坐标＝t﹣8（t＞4）；（3）存在符合题意的点N的坐标．①当AB＝AM时，在RT△MAH中，MH＝AMcos∠MAH＝AMcos∠ADO＝2，AH＝2，故点M的坐标为（﹣2，4+2），又∵MN平行且相等AB，设点N坐标为（x，y），则（x+0，y+4）＝（﹣2+8，4+2+0） ∴x＝8﹣2，y＝2，∴点N的坐标为（8﹣2，2）．②当BM＝AB时，设点M坐标为（x，﹣x+4），点N坐标为（a，b），∵四边形ABMN是菱形，点A（0，4），点B（8，0），∴（x+0，﹣x+4+4）＝（a+8，b+0），∴a＝x﹣8，b＝﹣x+8，即点N坐标为（x﹣8，﹣x+8），又∵BM＝AB＝4，∴＝4，解得：x＝12或x＝0，故此时点N的坐标为（4，﹣4）或（0，4）；③当AB为对角线时， 设点M坐标为（x，﹣x+4），则点N坐标为（8﹣x，x），∵此时AM＝AN，即可得：＝，解得：x＝，则此时点N的坐标为（，）．综上可得符合题意的点N的坐标为（8﹣2，2）或（0，4）或（4，﹣4）或（，）；10．【解答】解：（1）过点B作BF⊥x轴于F在Rt△BCF中∵∠BCO＝45°，BC＝12∴CF＝BF＝12∵C的坐标为（﹣18，0）∴AB＝OF＝6∴点B的坐标为（﹣6，12）．（2）过点D作DG⊥y轴于点G， ∵AB∥DG，∴△ODG∽△OBA，∵＝＝＝，AB＝6，OA＝12，∴DG＝4，OG＝8，∴D（﹣4，8），E（0，4）设直线DE解析式为y＝kx+b（k≠0）∴∴；∴直线DE解析式为y＝﹣x+4．（3）结论：存在．设直线y＝﹣x+4分别与x轴、y轴交于点E、点F，则E（0，4），F（4，0），OE＝OF＝4，EF＝4．如答图2所示，有四个菱形满足题意．①菱形OEP1Q1，此时OE为菱形一边．则有P1E＝P1Q1＝OE＝4，P1F＝EF﹣P1E＝4﹣4．易知△P1NF为等腰直角三角形，∴P1N＝NF＝P1F＝4﹣2；设P1Q1交x轴于点N，则NQ1＝P1Q1﹣P1N＝4﹣（4﹣2）＝2，又ON＝OF﹣NF＝2，∴Q1（2，﹣2）；②菱形OEP2Q2，此时OE为菱形一边．此时Q2与Q1关于原点对称，∴Q2（﹣2，2）；③菱形OEQ3P3，此时OE为菱形一边． 此时P3与点F重合，菱形OEQ3P3为正方形，∴Q3（4，4）；④菱形OP4EQ4，此时OE为菱形对角线．由菱形性质可知，P4Q4为OE的垂直平分线，由OE＝4，得P4纵坐标为2，代入直线解析式y＝﹣x+4得横坐标为2，则P4（2，2），由菱形性质可知，P4、Q4关于OE或y轴对称，∴Q4（﹣2，2）．综上所述，存在点Q，使以O、E、P、Q为顶点的四边形是菱形；点Q的坐标为：Q1（2，﹣2），Q2（﹣2，2），Q3（4，4），Q4（﹣2，2）．11．【解答】解：（1）∵DC是AB垂直平分线，OA垂直AB，∴G点为OB的中点， ∵OB＝，∴G（，0）．（2）过点C作CH⊥x轴于点H，在Rt△ABO中，∠ABO＝30°，OB＝，∴cos30°＝＝，即AB＝×＝4，又∵CD垂直平分AB，∴BC＝2，在Rt△CBH中，CH＝BC＝1，BH＝，∴OH＝﹣＝，∴C（，﹣1），∵∠DGO＝60°，∴OG＝OB＝，∴OD＝tan60°＝4，∴D（0，4），设直线CD的解析式为：y＝kx+b，则，解得： ∴y＝﹣x+4；（3）存在点Q、P，使得以O、D、P、Q为顶点的四边形是菱形．①如图，当OD＝DQ＝QP＝OP＝4时，四边形DOPQ为菱形，设QP交x轴于点E，在Rt△OEP中，OP＝4，∠OPE＝30°，∴OE＝2，PE＝2，∴Q（2，4﹣2）．②如图，当OD＝DQ＝QP＝OP＝4时，四边形DOPQ为菱形，延长QP交x轴于点F，在Rt△POF中，OP＝4，∠FPO＝30°，∴OF＝2，PF＝2，∴QF＝4+2∴Q（﹣2，4+2）． ③如图，当PD＝DQ＝QO＝OP＝时，四边形DOPQ为菱形，在Rt△DQM中，∠MDQ＝30°，∴MQ＝DQ＝∴Q（，2）．④如图，当OD＝OQ＝QP＝DP＝4时，四边形DOQP为菱形，设PQ交x轴于点N，此时∠NOQ＝∠ODQ＝30°，在Rt△ONQ中，NQ＝OQ＝2， ∴ON＝2，∴Q（2，﹣2）；综上所述，满足条件的点Q共有四点：（2，4﹣2），（﹣2，4+2），（，2），（2，﹣2）．12．【解答】解：（1）由已知得A点坐标（﹣4，0），B点坐标（0，4），∵OB＝OA，∴∠BAO＝60°，∵∠ABC＝60°，∴△ABC是等边三角形，∵OC＝OA＝4，∴C点坐标（4，0），设直线BC解析式为y＝kx+b，， ∴，∴直线BC的解析式为y＝﹣；2）当P点在AO之间运动时，作QH⊥x轴．∵，∴，∴QH＝t∴S△APQ＝AP•QH＝t•t＝t2（0＜t≤4），同理可得S△APQ＝t•（8）＝﹣（4≤t＜8）；（3）存在．∵S△APQ＝t•（8）＝﹣＝﹣（t﹣4）2+8，∴当t＝4时，△APQ的面积取得最大值，∵AO＝4，BC＝8，所以此时Q点和B点重合，①当AQ是菱形的边时，如图所示，M1，M2和M3所对应的菱形，在菱形AM1N1Q中，N1O＝AO＝4，所以N点的坐标为（4，0），在菱形AQM2N2中，AN2＝AQ＝8，所以N2点的坐标为（﹣4，8），在菱形AQM3N3中，AN3＝AB＝8，所以N3点的坐标为（﹣4，﹣8）， ②当AQ为菱形的对角线时，如图所示的菱形AM4QN4，设菱形的边长为x，则在Rt△AM4O中，AM42＝AO2+M4O2，即x2＝42+（4﹣x）2，解得x＝，所以N4（﹣4，）．综上可得，平面内满足条件的N点的坐标为（4，0）或（﹣4，8）或（﹣4，﹣8）或（﹣4，）．13．【解答】解：（1）解方程x2﹣4x+3＝0得x1＝1，x2＝3．依题意得点B的坐标是（﹣1，0），C（3，0）． （2）设CE的直线解析式为y＝kx+b，把点C，M的坐标代入可得⇒．得出CE的直线解析式为y＝x﹣3，又因为直线CE⊥AC，故直线AC的解析式为y＝﹣x+3．（3）存在．Q1（3，3）；Q2（）；Q3（）；Q4（，﹣）．14．【解答】解：（1）对于直线y＝﹣x+6，令x＝0，得到y＝6，可得A（0，6），令y＝0，得到x＝8，可得D（8，0），∴AC＝AO＝6，OD＝8，AD＝＝10，∴CD＝AD﹣AC＝4，设BC＝OB＝x，则BD＝8﹣x，在Rt△BCD中，∵BC2+CD2＝BD2，∴x2+42＝（8﹣x）2，∴x＝3，∴B（3，0）．（2）设直线AB的解析式为y＝kx+6，∵B（3，0），∴3k+6＝0，∴k＝﹣2，∴直线AB的解析式为y＝﹣2x+6， 作GM⊥x轴于M，FN⊥x轴于N，∵△DFG是等腰直角三角形，∴DG＝FD，∠1＝∠2，∠DMG＝∠FND＝90°，∴△DMG≌△FND（AAS），∴GM＝DN，DM＝FN，设GM＝DN＝m，DM＝FN＝n，∵G、F在直线AB上，则：m＝﹣2（8﹣n）+6，﹣n＝﹣2（8﹣m）+6，解得：m＝2，n＝6∴F（6，﹣6）．（3）①当点E在y轴左侧时，如图，设Q（a，﹣a+6），∵PQ∥x轴，且点P在直线y＝﹣2x+6上，∴P（a，﹣a+6），∴PQ＝a，作QH⊥x轴于H． ∴DH＝a﹣8，QH＝a﹣6，∴＝，由勾股定理可知：QH：DH：DQ＝3：4：5，∴QH＝DQ＝a，∴a＝a﹣6，∴a＝16，∴Q（16，﹣6），P（6，﹣6），∵ED∥PQ，ED＝PQ，D（8，0），∴E（﹣2，0）．②当点E在y轴右侧时，同理可得：点E（3.4，0）（舍去）；故点E的坐标为（﹣2，0）．