人教版九年级数学上册 第二十四章 园 单元复习

人教版九年级数学上册 第二十四章 园 单元复习

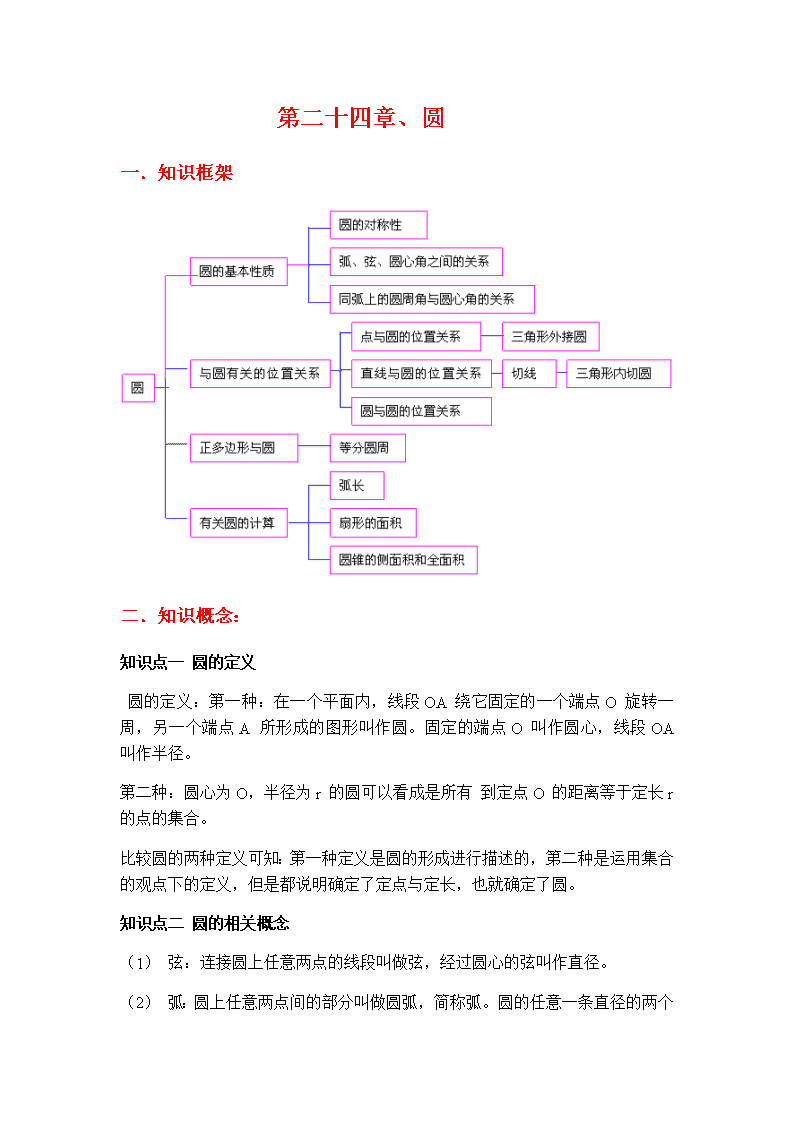
第二十四章、圆一．知识框架二．知识概念：知识点一圆的定义圆的定义：第一种：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫作圆。固定的端点O叫作圆心，线段OA叫作半径。第二种：圆心为O，半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合。比较圆的两种定义可知：第一种定义是圆的形成进行描述的，第二种是运用集合的观点下的定义，但是都说明确定了定点与定长，也就确定了圆。知识点二圆的相关概念（1）弦：连接圆上任意两点的线段叫做弦，经过圆心的弦叫作直径。（2） 弧：圆上任意两点间的部分叫做圆弧，简称弧。圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。（3）等圆：等够重合的两个圆叫做等圆。（4）等弧：在同圆或等圆中，能够互相重合的弧叫做等弧。弦是线段，弧是曲线，判断等弧首要的条件是在同圆或等圆中，只有在同圆或等圆中完全重合的弧才是等弧，而不是长度相等的弧。知识点三垂径定理C（1）垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧。如图所示，直径为CD，AB是弦，且CD⊥AB，BAMD垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧如上图所示，直径CD与非直径弦AB相交于点M，注意：因为圆的两条直径必须互相平分，所以垂径定理的推论中，被平分的弦必须不是直径，否则结论不成立。 典型例题：1.下列说法中正确的是(　B　)A．等弦所对的弧相等B．等弧所对的弦相等C．圆心角相等，它们所对的弦也相等D．等弦所对的圆心角相等2.下列说法中，正确的是(　B　)A．垂直于半径的直线是圆的切线B．经过半径的外端且垂直于这条半径的直线是圆的切线C．经过半径的端点且垂直于这条半径的直线是圆的切线D．到圆心的距离等于直径的直线是圆的切线3.如图，已知AB是半圆O的直径，弦CD∥ AB，点P，Q分别在线段OC，CD上，且DQ＝OP.求证：AP＝OQ.证明：连接OD.∵OC＝OD，∴∠C＝∠D.∵CD∥AB，∴∠C＝∠AOP，∴∠D＝∠AOP.又∵OP＝DQ，OA＝OD，∴△AOP≌△ODQ，∴AP＝OQ.知识点四弦、弧、圆心角的关系（1）弦、弧、圆心角之间的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。（2）在同圆或等圆中，如果两个圆心角，两条弧，两条弦中有一组量相等，那么它们所对应的其余的各组量也相等。（3）注意不能忽略同圆或等圆这个前提条件，如果丢掉这个条件，即使圆心角相等，所对的弧、弦也不一定相等，比如两个同心圆中，两个圆心角相同，但此时弧、弦不一定相等。知识点五圆周角定理 （1）圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。（2）圆周角定理的推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对弦是直径。（3）圆周角定理揭示了同弧或等弧所对的圆周角与圆心角的大小关系。“同弧或等弧”是不能改为“同弦或等弦”的，否则就不成立了，因为一条弦所对的圆周角有两类。典型例题：1.在半径为6cm的圆中，长为2πcm的弧所对的圆周角的度数为(　　)A．30°B．45°C．60°D．90°2.如图，点A，B，C在☉O上，BC=6，∠BAC=30°，则☉O的半径为　　　　. 3.若圆锥的侧面积是15π，母线长是5，则该圆锥底面圆的半径是_______．4.如图，⊙O的半径为3，P是CB延长线上一点，OP＝5，PA切⊙O于点A，则PA＝_______.知识点六圆内接四边形及其性质 圆内接多边形：如果一个多边形的所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆。圆内接四边形的性质：圆内接四边形的对角互补。典型例题：1.(2019•益阳)如图，PA、PB为圆O的切线，切点分别为A、B，PO交AB于点C，PO的延长线交圆O于点D，下列结论不一定成立的是()A．PA=PBB．∠BPD=∠APD C．AB⊥PDD．AB平分PD2.2019·安徽月考如图，正五边形ABCDE内接于⊙O，过点A作⊙O的切线交对角线DB的延长线于点F，则下列结论不成立的是(　　)A．AE∥BFB．AF∥CDC．DF＝AFD．AB＝BF知识点七点与圆的位置关系（1）点与圆的位置关系有：点在圆外，点在圆上，点在圆内三种。 （2）用数量关系表示：若设⊙O的半径是r，点P到圆的距离OP=d，则有：点P在圆外d＞r；点p在圆上d=r；点p在圆内d＜r。知识点八三角形的外接圆与外心（1）经过三角形三个顶点可以作一个圆，这个圆叫做三角形的外接圆。（2）外接圆的圆心是三角形三条边的垂直平分线的交点，叫做这个三角形的外心。知识点九反证法（1）反证法：假设命题的结论不成立，经过推理得出矛盾，由矛盾断定所作假设不正确，从而得到原命题成立，这种证明命题的方法叫做反证法。（2）反证法的一般步骤：①假设命题的结论不成立；②从假设出发，经过逻辑推理，推出或与定义，或与公理，或与定理，或与已知等相矛盾的结论；③由矛盾判定假设不正确，从而得出原命题正确。知识点十直线与圆的位置关系（1）直线与圆的位置关系有：相交、相切、相离三种。（2）直线与圆的位置关系可以用数量关系表示若设⊙O的半径是r，直线l与圆心0的距离为d，则有：直线l和⊙O相交d＜r；直线l和⊙O相切d=r；直线l和⊙O相离d＞r知识点十一切线的判定和性质 （1）切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。（2）切线的性质定理：圆的切线垂直于过切点的半径。（3）切线的其他性质：切线与圆只有一个公共点；切线到圆心的距离等于半径；经过圆心且垂直于切线的直线必过切点；必过切点且垂直于切线的直线必经过圆心。典型例题：1.如图，AB为⊙O的直径，C，D是半圆O的三等分点，过点C作AD延长线的垂线CE，垂足为E.(1)求证：CE是⊙O的切线；(2)若⊙O的半径为2，求图中阴影部分的面积．【答案】解：(1)证明：连接OC.∵C，D为半圆O的三等分点，∴＝＝，∴∠DAC＝∠BAC.∵OA＝OC，∴∠BAC＝∠ACO，∴∠DAC＝∠ACO，∴OC∥AD. ∵CE⊥AD，∴CE⊥OC，∴CE为⊙O的切线．(2)连接OD.∵＝＝，∴∠AOD＝∠COD＝∠BOC＝×180°＝60°.又∵OC＝OD，∴△COD为等边三角形，∴∠CDO＝60°＝∠AOD，∴CD∥AB，∴S△ACD＝S△COD，∴图中阴影部分的面积＝S扇形COD＝＝.知识点十二切线长定理（1）切线长的定义：经过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长。（2）切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。（3）注意：切线和切线长是两个完全不同的概念，必须弄清楚切线是直线，是不能度量的；切线长是一条线段的长，这条线段的两个端点一个是在圆外一点，另一个是切点。 典型例题：1.如图，△ABC是等边三角形，AO⊥BC，垂足为O，⊙O与AC相切于点D，BE⊥AB交AC的延长线于点E，与⊙O相交于G，F两点．(1)求证：AB与⊙O相切；(2)若等边三角形ABC的边长是4，求线段BF的长．解：(1)证明：如图，过点O作OM⊥AB，垂足为M.∵⊙O与AC相切于点D，∴OD⊥AC.∵△ABC是等边三角形，∴AB＝AC.又∵AO⊥BC，∴∠DAO＝∠MAO.又∵OM⊥AB，OD⊥AC，∴OM＝OD，∴AB与⊙O相切．(2)如图，过点O作ON⊥BE，垂足为N，连接OF.依题意得O是BC的中点，∴OB＝2.∵在Rt△OBM中，∠ABC＝60°，OB＝2，∴BM＝1，OM＝. ∵BE⊥AB，OM⊥AB，ON⊥BE，∴四边形OMBN是矩形，∴ON＝BM＝1，BN＝OM＝.在Rt△NOF中，∵OF＝OM＝，ON＝1，∴由勾股定理得NF＝，∴BF＝BN＋NF＝＋.知识点十三三角形的内切圆和内心（1）三角形的内切圆定义：与三角形各边都相切的圆叫做三角形的内切圆。这个三角形叫做圆的外切三角形。(2)三角形的内心：三角形内切圆的圆心叫做三角形的内心。(3)注意：三角形的内心是三角形三条角平分线的交点，所以当三角形的内心已知时，过三角形的顶点和内心的射线，必平分三角形的内角。典型例题：1、边长为6的正三角形的内切圆半径是__√3____，外接圆半径是2√32、如图，⊙O内切于△ABC，切点为D、E、F，若∠B=50°,∠C=60°，连接OE、OF、DE、DF，则∠EDF等于 3.如图，已知等腰直角三角形ABC，∠ACB＝90°，D是斜边AB的中点，且AC＝BC＝16分米，以点B为圆心，BD长为半径画弧，交BC于点F，以点C为圆心，CD长为半径画弧，与AC，BC分别交于点E，G.求阴影部分的面积．【答案】解：连接CD.∵△ABC是等腰直角三角形，D是斜边AB的中点，∴CD⊥AB.由已知，得AB＝16，∠DBF＝45°，∴BF＝BD＝AB＝CD＝8，∴阴影部分的面积是－－[×－]＝64(分米2)．答：阴影部分的面积是64平方分米．知识点十四圆与圆的位置关系（1）圆与圆的位置关系有五种：①如果两个圆没有公共点，就说这两个圆相离，包括外离和内含两种；②如果两个圆只有一个公共点，就说这两个圆相切，包括内切和外切两种；③如果两个圆有两个公共点，就说这两个圆相交。（2）圆与圆的位置关系可以用数量关系来表示：若设两圆圆心之间的距离为d，两圆的半径分别是r1r2,且r1＜r2，则有 ①两圆外离d＞r1+r2②两圆外切d=r1+r2③两圆相交r2-r1＜d＜r1+r2④两圆内切d=r2-r1⑤两圆内含d＜r2-r1典型例题：1、已知圆的半径r等于5厘米，点到圆心的距离为d，（1）当d＝2厘米时，有d__《__r，点在圆_____内_________（2）当d＝7厘米时，有d__》__r，点在圆____外__________（3）当d＝5厘米时，有d__=__r，点在圆______上________2、已知圆的半径r等于12厘米，圆心到直线l的距离为d，（1）当d＝10厘米时，有d__《__r，直线l与圆__相交__（2）当d＝12厘米时，有d_=___r，直线l与圆_相切___（3）当d＝15厘米时，有d__》__r，直线l与圆_相离___3、已知⊙O1的半径为6厘米，⊙O2的半径为8厘米，圆心距为d，则：R＋r＝___8厘米_____，R－r＝___2厘米_________；24.3正多边形和圆 知识点十五正多边形的外接圆和圆的内接正多边形正多边形与圆的关系非常密切，把圆分成n（n是大于2的自然数）等份，顺次连接各分点所得的多边形是这个圆的内接正多边形，这个圆就是这个正多边形的外接圆。正多边形的中心：一个正多边形的外接圆的圆心叫做这个正多边形的中心。正多边形的半径：外接圆的半径叫做正多边形的半径。正多边形的中心角：正多边形每一条边所对的圆心角叫做正多边形的中心角。正多边形的边心距：中心到正多边形一边的距离叫做正多边形的边心距。知识点十六正多边形的性质（1）正n边形的半径和边心距把正多边形分成2n个全等的直角三角形。（2）所有的正多边形都是轴对称图形，每个正n边形共有n条对称轴，每条对称轴都经过正n边形的中心；当正n边形的边数为偶数时，这个正n边形也是中心对称图形，正n边形的中心就是对称中心。（3）正n边形的每一个内角等于，中心角和外角相等，等于典型例题：1、如图，正五边形ABCDE的顶点都在⊙O上，P是上一点，则∠BPC=____36°_______2、如图，小明在操场上从点O出发，沿直线前进5米后向左转，再沿直线前进5米后，又向左转，……照这样走下去，他第一次回到出发地O点时，一共走了__45___米。 知识点十七弧长和扇形面积弧长公式在半径为R的圆中，360°的圆心角所对的弧长就是圆的周长C=2πR，所以n°的圆心角所对的弧长的计算公式。知识点十八扇形面积公式在半径为R的圆中，360°的圆心角所对的扇形面积就是圆的面积，所以圆心角为n°的扇形的面积为。比较扇形的弧长公式和面积公式发现：所以知识点十九圆锥的侧面积和全面积圆锥的侧面积是曲面，沿着圆锥的一条母线将圆锥的侧面展开，容易得到圆锥的侧面展开图是一个扇形。设圆锥的母线长为l，底面圆的半径为r，那么这个扇形的半径为l，扇形的弧长为2πr，因此圆锥的侧面积圆锥侧。圆锥的全面积为。 典型例题：(答案保留π)1.如图中的小方格都是边长为1的正方形，则以格点为圆心，半径为1和2的两种弧围成的“叶状”(阴影部分)图案的面积为__2π－4　______．2.如图，分别以正三角形的3个顶点为圆心，边长为半径画弧，三段弧围成的图形称为莱洛三角形．若正三角形的边长为6cm，则该莱洛三角形的周长为___6π_____cm.第二十四章圆单元复习练习题一、选择题1．如图，C为线段BE上一动点不与点B，E重合，在BE同侧分别作等边ABC和等边CDE、BD与AE交于点P，BD与AC交于点M，AE与CD交于点N，连结MN．以下四个结论：①CM=CN；②∠APB=60°；③PA+PC=PB；④PC平分∠BPE；恒成立的结论有（） A．①②④B．①②③④C．①③④D．①④2．如图，在正方形ABCD中，BC=2，点P，Q均为AB边上的动点，BE⊥CP，垂足为E，则QD+QE的最小值为（）A．2B．3C．D．3．如图,点A是以BC为直径的半圆的中点，连接AB，点D是直径BC上一点，连接AD，分别过点B、点C向AD作垂线，垂足为E和F，其中，EF=2，CF=6，BE=8，则AB的长是（）A．4B．6C．8D．104．如图，以等边的一边为直径的半圆交于点，交于点，若，则阴影部分的面积是（　　） A．B．C．D．5．如图，在中，直径垂直弦于点，且.点为上一点（点不与点，重合），连结，，，，.过点作于点.给出下列结论:①是等边三角形；②在点从的运动过程中，的值始终等于.则下列说法正确的是（）A．①，②都对B．①对，②错C．①错，②对D．①，②都错6．如图，在平面直角坐标系中,若在直线上存在点满足,则的取值范围是（）A．B．C．D．7．如图，DB=DC,∠BAC=∠BDC=120°，DM⊥AC，E为BA延长线上的点，∠BAC的角平分线交BC于N，∠ABC的外角平分线交CA的延长线于点P，连接PN交AB于K，连接CK，则下列结论正确的是：①∠ABD=∠ACD；②DA平分∠EAC；③当点A在DB左侧运动时，为定值；④∠CKN=30°() A．①③④B．②③④C．①②④D．①②③8．已知⊙O的半径为13，弦AB∥CD，AB=24，CD=10，则四边形ACDB的面积是（　　）A．119B．289C．77或119D．119或2899．如图，在平面直角坐标系中，Q（3，4），P是在以Q为圆心，2为半径的⊙Q上一动点，设P点的横坐标为x，A（1，0）、B（-1，0），连接PA、PB，则PA2+PB2的最大值是A．64B．98C．100D．12410．如图，△ABC中，AC＝3，BC＝，∠ACB＝60°，过点A作BC的平行线l，P为直线l上一动点，⊙O为△APC的外接圆，直线BP交⊙O于E点，则AE的最小值为（）A．-1B．7-4C．D．1二、填空题11．如图，⊙O是△ABC的外接圆，AO⊥BC于F，D为的中点，E是BA延长线上一点，若∠DAE＝，则∠CAD＝_______． 12．如图，在Rt△中，，，，点是平面内到点的距离等于4的任意一点，点是的中点，则的取值范围是______．13．如图，AB为⊙O的直径，C为⊙O上一点，其中AB=4，∠AOC=120°，P为⊙O上的动点，连接AP，取AP中点Q，连CQ，则线段CQ的最大值为__________14．如图，∠AOB=45°，点P、Q都在射线OA上，OP=2，OQ=6．M是射线OB上的一个动点，过P、Q、M三点作圆，当该圆与OB相切时，其半径的长为______．15．如图，正方形中，为中点，，，交于，则的度数为_________． 三、解答题16．如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于、、、四点，点坐标为．抛物线与轴交于点，与直线交于点、，且、分别与圆相切于点和点．（1）求抛物线的解析式．（2）过点作圆的切线交的延长线于点，判断点是否在抛物线上，说明理由．（3）抛物线对称轴交轴于点，连接并延长交于点，求点的坐标．17． 我们知道，圆可以看成到定点的距离等于定长的点的集合．我们又知道了在平面内点与圆有三种位置关系．如图1，点P在⊙O外，点A是⊙O上一个动点，连接PO交⊙O于点B，我们发现，当点A与点B重合时，线段PA长最短．（1）利用图1，说明PA>PB；（2）如图2，一架10米长的梯子沿墙壁下滑，一只距离墙壁12米，距离地面5米的小鸟看到梯子的中点位置有食物，小鸟想用最短时间吃到食物，请在图中画出小鸟飞行的路径，并计算出小鸟飞行的距离；（3）如图3，矩形ABCD中，AB=2，AD=3，点E、F分别为AD、DC边上的点，且EF=2，点G为EF的中点，点P为BC上一动点，直接写出PA+PG的最小值． 18．如图1所示，在中，，，以所在直线为轴，边的垂直平分线为轴建立平面直角坐标系，将绕点顺时针旋转．（1）填空：当点旋转到轴正半轴时，则旋转后点坐标为______；（2）如图2所示，若边与轴交点为，边与直线的交点为，求证：的周长为定值；（3）在（2）的条件下，求内切圆半径的最大值． 19．如图1，中，，，为内一点，将绕点按逆时针方向旋转角得到，点的对应点分别为点，且三点在同一直线上．（1）填空：______（用含的代数式表示）；（2）如图2，若，请补全图形，再过点作于点，然后探究线段，，之间的数量关系，并证明你的结论； （3）如图3，若，，直接写出四边形面积的最大值______．20．如图，凸四边形ABCD中，AD＝BD，AD⊥BD． （1）若BC//AD，以顶点D为圆心，DA的长为半径作圆，请指出⊙D与直线BC的位置关系，并说明理由；（2）当AB＝2，∠BCD＝30°时，求四边形ABCD的面积的最大值；（3）若BC＝1，CD＝2，AC＝3，求∠BCD的度数． 21．如图，抛物线y＝x2+bx+c与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为M，对称轴交x轴于E，点D在第一象限，且在抛物线的对称轴上，DE＝OC，DM＝．（1）求抛物线的对称轴方程；（2）若DA＝DC，求抛物线的解析式；（3）在（2）的条件下，点P是抛物线对称轴上的一个动点，若在直线BM上只存在一个点Q，使∠PQC＝45°，求点P的坐标．