2012年广西自治区梧州市中考数学试题（含答案）

2012年广西自治区梧州市中考数学试题（含答案）

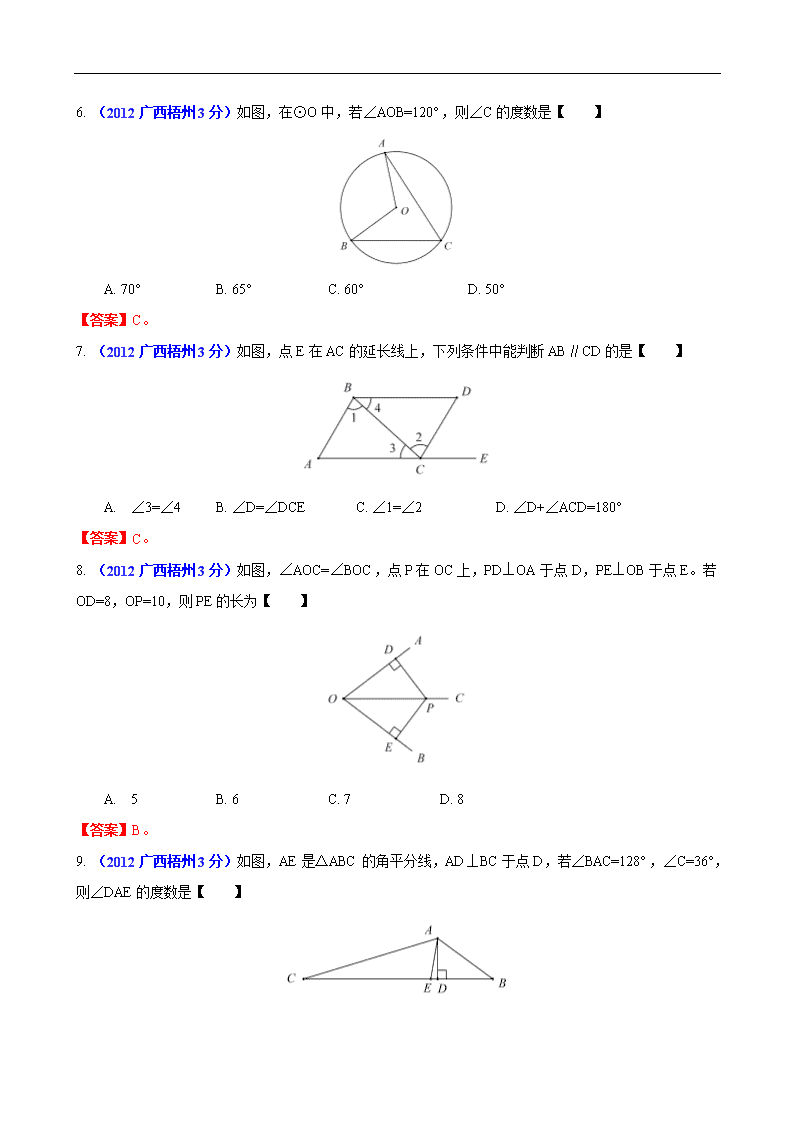
‎2012年中考数学试题（广西梧州卷）‎ ‎（本试卷满分120分，考试时间120分钟）‎ 一、选择题（本大题共12小题，每小题3分，共36分。在每小题给出的四个选项中，只有一项是正确的，每小题选对得3分，选错、不选或多选均得零分。‎ ‎1.（2012广西梧州3分）等于【 】‎ ‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】C。‎ ‎2. （2012广西梧州3分）某个物体的三视图形状、大小相同，则这个物体可能是【 】‎ ‎ A. 圆柱 B. 圆锥 C. 三棱柱 D. 球 ‎【答案】D。‎ ‎3. （2012广西梧州3分）我市某镇被自治区列为五个重点建设的广西特色工贸强镇之一。按规划，该镇 造1 000 000 000元特色工业集中区。把数1 000 000 000用科学记数法表示为【 】‎ ‎ A. 1.0×106 B. 1.0×107 C. 1.0×108 D. 1.0×109 ‎ ‎【答案】D。‎ ‎4. （2012广西梧州3分）下面调查中，适宜采用全面调查方式的是【 】‎ ‎ A. 调查亚洲中小学生身体素质状况 ‎ B. 调查梧州市冷饮市场某种品牌冰淇淋的质量情况 ‎ C. 调查某校甲班学生出生日期 ‎ D. 调查我国居民对汽车废气污染环境的看法 ‎【答案】C ‎5. （2012广西梧州3分）如图，直线AB和CD相交于点O，若∠AOC=125°，则∠AOD=【 】‎ ‎ A. 50° B. 55° C. 60° D. 65°‎ ‎【答案】B。‎ ‎6. （2012广西梧州3分）如图，在⊙O中，若∠AOB=120°，则∠C的度数是【 】‎ ‎ A. 70° B. 65° C. 60° D. 50°‎ ‎【答案】C。‎ ‎7. （2012广西梧州3分）如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是【 】‎ ‎ A. ∠3=∠4 B. ∠D=∠DCE C. ∠1=∠2 D. ∠D+∠ACD=180°‎ ‎【答案】C。‎ ‎8. （2012广西梧州3分）如图，∠AOC=∠BOC，点P在OC上，PD⊥OA于点D，PE⊥OB于点E。若 OD=8，OP=10，则PE的长为【 】‎ ‎ A. 5 B. 6 C. 7 D. 8‎ ‎【答案】B。‎ ‎9. （2012广西梧州3分）如图，AE是△ABC的角平分线，AD⊥BC于点D，若∠BAC=128°，∠C=36°，‎ 则∠DAE的度数是【 】‎ ‎ A. 10° B. 12° C. 15° D. 18°‎ ‎【答案】A。‎ ‎10. （2012广西梧州3分）关于x的分式方程无解，则m的值是【 】‎ ‎ A. 1 B. 0 C. 2 D. –2‎ ‎【答案】A。‎ ‎11. （2012广西梧州3分）关于x的一元二次方程(a+1) x2–4x–1=0有两个不相等的实数根，则a的取值范 围是【 】‎ ‎ A. a>–5 B. a>–5且a≠–1 C. a<–5 D. a≥–5且a≠–1‎ ‎【答案】B。‎ ‎12. （2012广西梧州3分）直线y=kx+k（k为正整数）与坐标轴所构成的直角三角形的面积为Sk，当k 分别为1，2，3，…，199，200时，则S1+S2+S3+…+S199+S200=【 】‎ ‎ A. 10000 B. 10050 C. 10100 D 10150‎ ‎【答案】B。‎ 二、填空题（本大题共6小题，每小题3分，共18分。）‎ ‎13. （2012广西梧州3分）方程x–5=0的解是x= ▲ ‎ ‎【答案】5。‎ ‎14. （2012广西梧州3分）计算： ▲ ‎ ‎【答案】2。‎ ‎15. （2012广西梧州3分）如图，在△ABC中，AB=AD=DC，∠BAD=32°，则∠BAC= ▲ ‎ ‎【答案】69°。‎ ‎16. （2012广西梧州3分）如图，正方形ABCD的边长为4，点A的坐标为（–1，1），AB平行于x轴，‎ 则点C的坐标为 ▲ ‎ ‎【答案】（3，5）。‎ ‎17. （2012广西梧州3分）如图，A点是y轴正半轴上一点，过点A作x轴的平行线交反比例函数的图象于点B，交反比例函数的图象于点C，若AB：AC=3：2，则k的值是 ▲ ‎ ‎【答案】。‎ ‎18. （2012广西梧州3分）如图，在矩形ABCD中，AB=6，BC=8，以D为旋转中心，顺时针旋转180°‎ 后停止，矩形ABCD在旋转过程中所扫过的面积是 ▲ ‎ ‎【答案】。‎ 三、解答题（本大题共8小题，满分66分）‎ ‎19. （2012广西梧州6分）化简：‎ ‎【答案】解：。‎ ‎20. （2012广西梧州6分）某电脑店有A、B两种型号的打印机和C、D、E三种芯片出售。每种型号的 打印机均需要一种芯片配套才能打印。‎ ‎（1）下列是该店用树形图或列表设计的配套方案，①的位置应填写______，②的位置应填写______‎ ‎（2）若仅有B型打印机与E种芯片不配套，则上面（1）中的方案配套成功率是______‎ ‎ 芯片 ‎ 配套方案 打印机 C D E A ‎(A,C)‎ ‎(A,D)‎ ‎②‎ B ‎(B,C)‎ ‎(B,D)‎ ‎(B,E)‎ ‎【答案】解；（1）E；（A，E）。‎ ‎ （2）。‎ ‎21. （2012广西梧州8分）如图，某校为搞好新校区的绿化，需要移植树木。该校九年级数学兴趣小组对 某棵树木进行测量，此树木在移植时需要留出根部（即CD）1.3米。他们在距离树木5米的E点观测（即 CE=5米），测量仪的高度EF=1.2米，测得树顶A的仰角∠BFA=40°，求此树的整体高度AD。（精确到0.1‎ 米）（参考数据：sin40°=0.6428， cos40°=0.7660，tan40°=0.8391）‎ ‎【答案】解：在矩形BCEF中，BC=EF=1.2，BF=EC=5，‎ 在Rt△ABF中，tan∠BFA=，即tan40°=，‎ ‎ ∴AB=BF×tan40°=5×0.8391=4.1955，‎ ‎ AD=AB+BC+CD=4.1955+1.2+1.3=6.6955≈6.7。‎ ‎ 答：此树的整体高度约为6.7米。‎ ‎22. （2012广西梧州8分）如图，等腰梯形ABCD中，AD∥BC，点E是AD延长线上的一点，且CE=CD。‎ 求证：∠B=∠E ‎【答案】证明：∵四边形ABCD是等腰梯形，∴∠B=∠1。‎ ‎ ∵AD∥BC，∴∠1=∠2。‎ ‎ ∵CE=CD，∴∠2=∠E。‎ ‎∴∠B=∠E。‎ ‎23. （2012广西梧州8分）今年5月，在中国武汉举办了汤姆斯杯羽毛球团体赛。在27日的决赛中，中 国队占胜韩国队夺得了冠军。某羽毛球协会组织一些会员到现场观看了该场比赛。已知该协会购买了每张 ‎300元和每张400元的两种门票共8张，总费用为2700元。请问该协会购买了这两种门票各多少张？‎ ‎【答案】解：设每张300元的门票买了x张，则每张400元的门票买了（8–x）张，根据题意得 ‎ 300x+400(8–x)=2700‎ ‎ 解得，x=5。‎ ‎ 8–x=8–5=3。‎ 答：每张300元的门票购买了5张，每张400元的门票购买了3张。‎ ‎24. （2012广西梧州10分）某文具店到批发市场选购A、B两种文具，批发价分别为14元/个、10元/个。‎ 若该店零售A、B两种文具的每天销量y（个）与零售价x（元/个）都是一次函数y=kx+20的关系，如图 所示。‎ ‎（1）求此一次函数的关系式；‎ ‎（2）现批发市场进行促销活动，凭会员卡（240元/张）在该批发市场购买所有物品均进行打折优惠，若 文具店购买A、B两种文具各50个，问打折小于多少折时，采用购买会员卡的方式合算；‎ ‎（3）在文具店不购买会员卡的情况下，若A种文具零售价比B种文具零售价高2元/个，求这两种文具每 天的销售总利润W(元)与A种文具零售价x（元/个）之间的函数关系式，并说明当A种文具的零售价为多 少时，每天的销售利润最大。‎ ‎（说明：本题不要求写出自变量x的取值范围）‎ ‎【答案】解：（1）根据题意，把（10，10）代入y=kx+20得10=10k+20，k= –1。‎ ‎ ∴一次函数的关系式为y= –x+20。‎ ‎（2）设打折为a折时，购买会员卡的方式合算，依题意得，‎ ‎ 50×14×0.1a+50×10×0.1a<50×14+50×10，‎ ‎ 解得，a<8。‎ ‎ 答：当打折小于8折时，采用购买会员卡的方式合算。‎ ‎（3）W=(x–14)(–x+20)+(x–2––10)[–(x–2)+20]= –2(x–17)2+34。‎ ‎ ∴当x=17时，每天的销售利润W最大。‎ ‎25. （2012广西梧州10分）如图，AB是⊙O的直径，CO⊥AB于点O，CD是⊙O的切线，切点为D.连 接BD，交OC于点E。‎ ‎（1）求证：∠CDE=∠CED；‎ ‎（2）若AB=13，BD=12，求DE的长。‎ ‎【答案】解：（1）证明：连接OD，‎ ‎ ∵CD是⊙O的是切线，∴∠ODC=90°。‎ ‎ ∵OD=OB，∴∠B=∠ODB。‎ ‎∵OC⊥AB，∴∠CED=∠OEB=90°–∠B。‎ ‎ 又∵∠CDE=90°–∠ODB，∴∠CDE=∠CED。‎ ‎（2）连接AD，‎ ‎∵AB是⊙O的直径，∴∠ADB=90°。‎ ‎ ∵AB=13，∴OB=。‎ ‎ ∵∠ADB=∠BOE=90°，∠B=∠B，∴△ABD∽△EBO。‎ ‎ ∴。∴。∴EB=。‎ ‎∴DE=BD–EB=12–=，即DE的长为。‎ ‎26. （2012广西梧州10分）如图，抛物线的顶点为A，对称轴AB与x轴交于点B.‎ 在x轴上方的抛物线上有C、D两点，它们关于AB对称，并且C点在对称轴的左侧，CB⊥DB。‎ ‎（1）求出此抛物线的对称轴和顶点A的坐标；‎ ‎（2）在抛物线的对称轴上找出点Q，使它到A、C两点的距离相等，并求出点Q的坐标；‎ ‎（3）延长DB交抛物线于点E，在抛物线上是否存在点P，使得△DEP的面积等于△DEC的面积，若存 在，请你直接写出点P的坐标，若不存在，请说明理由。‎ ‎【提示：抛物线的对称轴为，顶点坐标为】‎ ‎【答案】解：（1）∵‎ ‎ ∴此抛物线的对称轴为x=6，顶点A的坐标（6，6）。‎ ‎（2）过C作CG⊥x轴于G，CD交AB于点J。‎ ‎∵C、D关于AB对称，‎ ‎ ∴BC=BD，CD∥x轴。‎ ‎ 又∵CB⊥DB，‎ ‎ ∴△BCD是等腰直角三角形。‎ ‎ ∴∠DCB=∠CBO=45°。‎ ‎ ∴△BCG为等腰直角三角形。‎ ‎ ∴GB=GC。‎ ‎ 设C的横坐标为a，则GC=GB=6–a。‎ ‎ 将C（a，6–a）代入得6–a= –a2+12a–30，‎ ‎ 解得，a=4，a=9（不符合题意，舍去）。‎ ‎ ∴C（4，2）。‎ 设Q（6，m）则AQ=6–m，CQ=。‎ ‎ ∵AQ=CQ，∴=6–m，解得m=。‎ ‎ ∴Q（6，）。‎ ‎（3）存在。P1（7，5）；P2（）；P3（）。‎