2020九年级数学上册 第一章 二次函数检测卷同步测试 （新版）浙教版

2020九年级数学上册 第一章 二次函数检测卷同步测试 （新版）浙教版

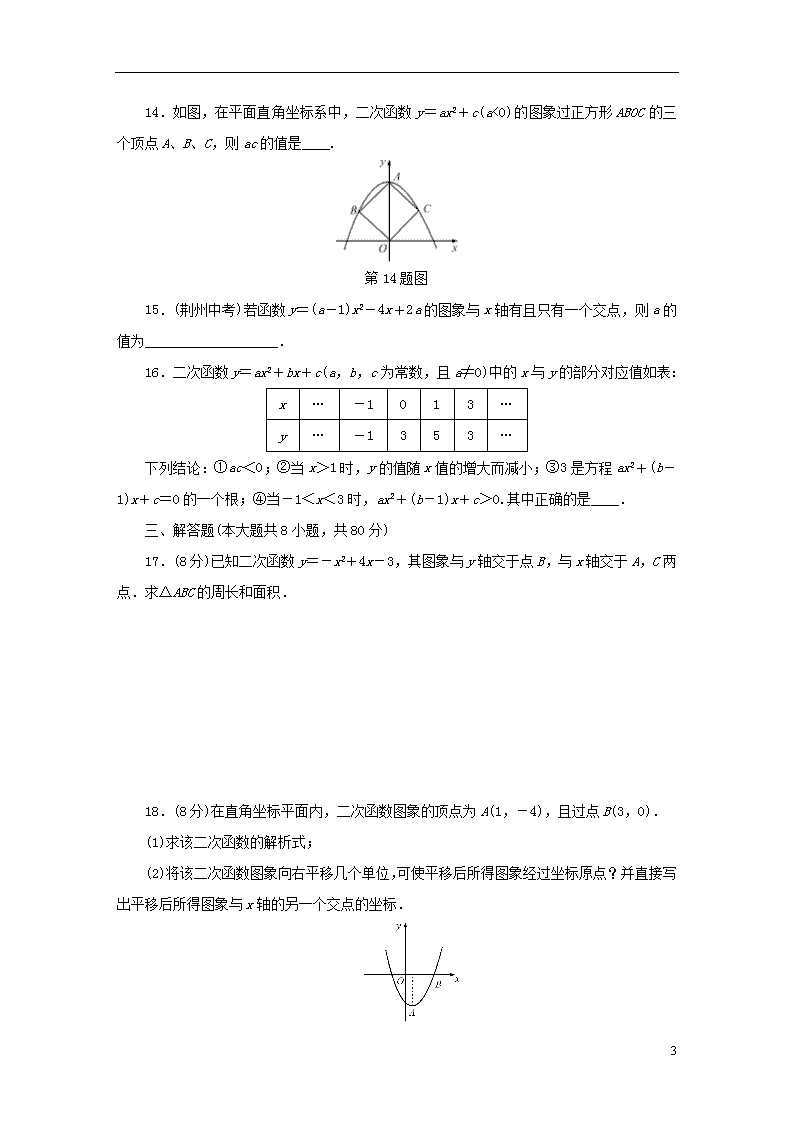
第1章　二次函数检测卷 一、选择题(本大题共10小题，每小题4分，共40分)‎ ‎1．下列各点不在抛物线y＝x2－2图象上的是( )‎ A．(－1，－1) B．(2，2) C．(－2，0) D．(0，－2)‎ ‎2．二次函数y＝(x－3)(x＋2)的图象的对称轴是( )‎ A．x＝3 B．x＝－‎2 C．x＝－ D．x＝ ‎3．抛物线y＝－3x2＋2x－1与坐标轴的交点个数为( )‎ A．0个 B．1个 C．2个 D．3个 ‎4．童装专卖店销售一种童装，若这种童装每天获利y(元)与销售单价x(元)满足关系y＝－x2＋50x－500，若要想获得最大利润，则销售单价x为( )‎ A．25元 B．20元 C．30元 D．40元 5． 二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，则下列结论中正确的是( )‎ 第5题图 A．a＞0 ‎ B．当－1＜x＜3时，y＞0‎ C．c＜0 ‎ D．当x≥1时，y随x的增大而增大 ‎6．若A(－，y1)、B(－1，y2)、C(，y3)为二次函数y＝－x2－4x＋k的图象上的三点，则y1、y2、y3的大小关系是( )‎ A．y1＜y2＜y3 B．y3＜y2＜y‎1 C．y3＜y1＜y2 D．y2＜y1＜y3‎ ‎7．把抛物线y＝2x2先向左平移3个单位，再向上平移4个单位，所得抛物线的函数表达式为( )‎ A．y＝2(x＋3)2＋4 B．y＝2(x＋3)2－4‎ C．y＝2(x－3)2－4 D．y＝2(x－3)2＋4‎ ‎8．若二次方程(x－a)(x－b)－2＝0的两根是m，n，且a0，且m≠2)．‎ 第24题图 ‎(1)求这条抛物线的解析式；‎ ‎(2)求矩形PQMN的周长C与m之间的函数关系式；‎ ‎(3)当矩形PQMN是正方形时，求m的值．‎ 活页参考答案 上册 第1章　二次函数检测卷 1． C 2.D 3.B 4.A 5.B 6.C 7.A 8.A 9.B 10.D ‎ ‎11.6 ‎ ‎12.y＝－x2＋3x＋4或y＝x2－3x－4‎ ‎13．12 ‎ ‎14.－2 ‎ ‎15.－1或2或1 ‎ ‎16.①③④ ‎ ‎17.令x＝0，得y＝－3，故B点坐标为(0，－3)，解方程－x2＋4x－3＝0，得x1＝1，x2‎ 10‎ ‎＝3.故A、C两点的坐标为(1，0)，(3，0)．所以AC＝3－1＝2，AB＝＝，BC＝＝3，OB＝│－3│＝3.C△ABC＝AB＋BC＋AC＝2＋＋3；S△ABC＝AC·OB＝×2×3＝3. ‎ ‎18.(1)y＝(x－1)2－4，即y＝x2－2x－3; (2)令y＝0，得x2－2x－3＝0，解方程，得x1＝－1，x2＝3.所以二次函数图象与x轴的两个交点坐标分别为(3，0)和(－1，0)．所以二次函数图象向右平移1个单位后经过坐标原点．平移后所得图象与x轴的另一个交点坐标为(4，0)．‎ ‎19．(1)a＝3时，方程组为②×2得，4x－2y＝2③，①＋③得，5x＝5，解得x＝1，把x＝1代入①得，1＋2y＝3，解得y＝1，所以，方程组的解是 (2)方程组的两个方程相加得，3x＋y＝a＋1，所以S＝a(3x＋y)＝a(a＋1)＝a2＋a，所以，当a＝－＝－时，S有最小值．　‎ ‎20.‎ 第20题图 ‎(1)过点A作AC⊥x轴，过点B作BD⊥x轴，垂足分别为C，D，则∠ACO＝∠ODB＝90°，∴∠AOC＋∠OAC＝90°.∵∠AOB＝90°，∴∠AOC＋∠BOD＝90°.∴∠OAC＝∠BOD.又∵AO＝BO，∴△ACO≌△ODB(AAS)．∴OD＝AC＝1，DB＝OC＝3.∴点B的坐标为(1，3)；　(2)∵抛物线过原点，∴可设抛物线的函数表达式为y＝ax2＋bx.将点A(－3，1)，B(1，3)的坐标代入，得解得∴所求抛物线的函数表达式为y＝x2＋x; (3)由(2)得，抛物线的对称轴为直线x＝－，点B的坐标为(1，3)，∴点B′的坐标为.设BB′边上的高为h，则h＝3－1＝2.|BB′|＝1＋＝.∴S△AB′B＝·h＝××2＝.‎ ‎21．(1)根据题意可知，抛物线经过(0，)，顶点坐标为(4，4)，则可设其解析式为y＝a(x－4)2＋4，解得a＝－.则所求抛物线的解析式为y＝－(x－4)2＋4.又篮圈的坐标是(7，3)，‎ 10‎ 代入解析式得，y＝－(7－4)2＋4＝3.所以能够投中；　(2)当x＝1时，y＝3，此时3.1＞3，故乙队员能够拦截成功．　‎ ‎22.(1)∵令y＝0得：x2＋x＝0，解得：x1＝0，x2＝－1，∴抛物线与x轴的交点坐标为(0，0)，(－1，0)．作直线y＝1，交抛物线于A、B两点，分别过A、B两点，作AC⊥x轴，垂足为C，BD⊥x轴，垂足为D，点C和点D的横坐标即为方程的根．根据图1可知方程的解为x1≈－1.6，x2≈0.6；　(2)∵将x＝0代入y＝x＋得y＝，将x＝1代入得：y＝2，∴直线y＝x＋经过点(0，)，(1，2)．直线y＝x＋的图象如图2所示，由函数图象可知：当x＜－1.5或x＞1时，一次函数的值小于二次函数的值；(3)先向上平移个单位，再向左平移个单位，平移后的顶点坐标为P(－1，1)．平移后的表达式为y＝(x＋1)2＋1，即y＝x2＋2x＋2.点P在y＝x＋的函数图象上．理由：∵把x＝－1代入得y＝1，∴点P的坐标符合直线的解析式．∴点P在直线y＝x＋的函数图象上．‎ ‎　　‎ 第22题图 ‎23．(1)根据表格中数据可得出：y与x是一次函数关系，设解析式为：y＝ax＋b，则解得： ‎∴函数解析式为：y＝－x＋8; (2)根据题意得：z＝(x－20)y－40＝(x－20)(－x＋8)－40＝－x2＋10x－200＝－(x2－100x)－200＝－[(x－50)2－2500]－200＝－(x－50)2＋50，∵－＜0，∴x＝50，z最大＝50.∴该公司销售这种计算器的净得利润z与销售价格x的函数解析式为z＝－x2＋10x－200，销售价格定为50元/个时净得利润最大，最大值是50万元； ‎ 10‎ 第23题图 ‎(3)当公司要求净得利润为40万元时，即－(x－50)2＋50＝40，解得：x1＝40，x2＝60.作函数图象的草图，通过观察函数y＝－(x－50)2＋50的图象，可知按照公司要求使净得利润不低于40万元，则销售价格的取值范围为：40≤x≤60.而y与x的函数关系式为：y＝－x＋8，y随x的增大而减少，∴若还需考虑销售量尽可能大，销售价格应定为40元/个．‎ ‎24．(1)把A(3，0)、B(2，2)两点坐标代入y＝ax2＋bx，得计算得出故抛物线所对应的函数表达式为y＝－x2＋3x. (2)∵点P在抛物线y＝－x2＋3x上，∴可以设P(m，－m2＋‎3m)，∵PQ∥y轴，∴Q(m，m)．①当02时，如图2中，PQ＝m－(－m2＋‎3m)＝m2－‎2m，C＝2(m2－‎2m)＋2＝‎2m2‎－‎4m＋2. (3)∵矩形PQMN是正方形，∴PQ＝PN＝1，当02时，如图4中，m2－‎2m＝1，计算得出m＝1＋(或1－不合题意舍弃)．‎ ‎ ‎ ‎ ‎ 第24题图 10‎