2020八年级数学上册第13章13

2020八年级数学上册第13章13

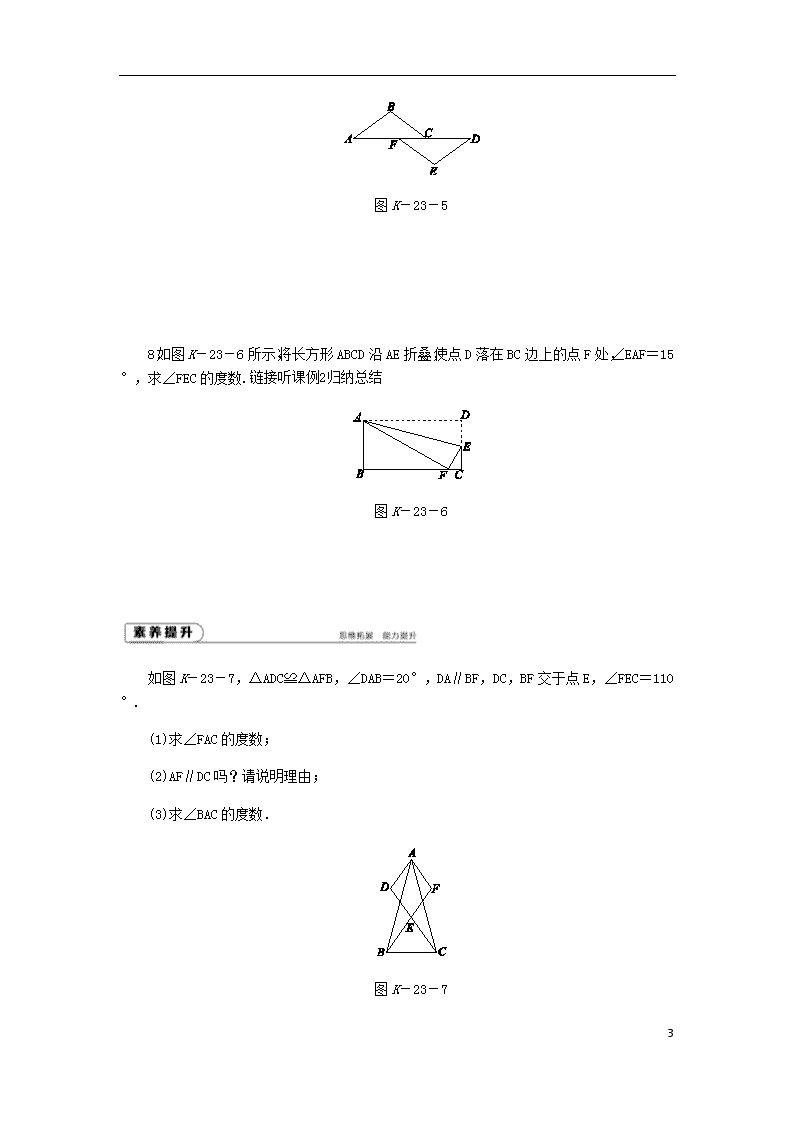
‎ [13.2　1.全等三角形　2.全等三角形的判定条件]‎ ‎　　　　　　　　　　　‎ 一、选择题 ‎1．已知△ABC≌△DEF，且∠A与∠D是对应角，∠C与∠F是对应角，则下列说法中正确的是(　　)‎ A．AC与DF是对应边　B．AC与DE是对应边 C．AC与EF是对应边　D．不能确定 ‎2．下列说法正确的有(　　)‎ ‎(1)如果两个三角形的一个角对应相等，那么它们全等；(2) 如果两个三角形有一边相等，那么它们全等； (3)如果两个三角形的三个角对应相等，那么它们全等；(4)如果两个三角形的两边对应相等，那么它们全等；(5)如果两个三角形的三个角对应相等，三条边也对应相等，那么它们全等．‎ A．1个 B．2个 C．3个 D．4个 ‎3．2017·长春朝阳期中如图K－23－1，△ABE≌△ACF.若AB＝5，AE＝2，则CE的长度是(　　)‎ A．2 B．‎3 C．25 D．5‎ 图K－23－1‎ ‎4.如图K－23－2，在△ABC中，∠BAC＝90°，将△ABC绕点C按逆时针方向旋转48°得到△A′B′C，点A在边B′C上，则∠B′的度数为(　　)‎ ‎　　　‎ 6‎ 图K－23－2‎ A．42° B．48° C．52° D．58°‎ 二、填空题 ‎5．如图K－23－3，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B的度数为________．‎ 图K－23－3‎ ‎.如图K－23－4，△ADE≌△CBF，若AD＝‎8 cm，CD＝‎5 cm，则BD的长为________．‎ ‎　　　‎ 图K－23－4‎ 三、解答题 ‎7．如图K－23－5，图中的两个三角形是全等三角形，其中A和D，B和E是对应点．‎ ‎(1)用符号“≌”表示这两个三角形全等(要求对应顶点写在对应位置上)；‎ ‎(2)写出图中相等的线段和相等的角；‎ ‎(3)写出图中互相平行的线段，并说明理由．‎ 6‎ 图K－23－5‎ ‎8．如图K－23－6所示，将长方形ABCD沿AE折叠，使点D落在BC边上的点F处，∠EAF＝15°，求∠FEC的度数. 图K－23－6‎ ‎　　　　　　　　‎ 如图K－23－7，△ADC≌△AFB，∠DAB＝20°，DA∥BF，DC，BF交于点E，∠FEC＝110°.‎ ‎(1)求∠FAC的度数；‎ ‎(2)AF∥DC吗？请说明理由；‎ ‎(3)求∠BAC的度数．‎ 图K－23－7‎ 6‎ 6‎ 详解详析 ‎【课时作业】‎ ‎[课堂达标]‎ ‎1．A ‎2．A ‎3．[解析] B　∵△ABE≌△ACF，∴AB＝AC＝5，∴CE＝AC－AE＝5－2＝3.‎ ‎4．[解析] A　∵在△ABC中，∠BAC＝90°，将△ABC绕点C按逆时针方向旋转48°得到△A′B′C，∴∠A′＝∠BAC＝90°，∠ACA′＝48°，∴∠B′＝90°－∠ACA′＝42°.故选A.‎ ‎5．120°‎ ‎6．[答案] ‎‎3 cm ‎[解析] ∵△ADE≌△CBF，∴AD＝CB.‎ 又∵AD＝AC＋CD，CB＝BD＋CD，‎ ‎∴BD＝AC＝AD－CD＝‎3 cm.‎ 故BD的长为‎3 cm.‎ ‎7．解：(1)△ABC≌△DEF.‎ ‎(2)相等的线段：AB＝DE，BC＝EF，AC＝DF，AF＝DC；相等的角：∠A＝∠D，∠B＝∠E，∠ACB＝∠DFE，∠BCD＝∠EFA.‎ ‎(3)BC∥EF，AB∥DE.‎ 理由：∵△ABC≌△DEF，‎ ‎∴∠A＝∠D，∠ACB＝∠DFE，‎ ‎∴AB∥DE，BC∥EF.‎ ‎8．[导学号：90702252]‎ 解：由题意知△AFE与△ADE关于直线AE对称，∴△AFE≌△ADE，‎ 6‎ ‎∴∠EAF＝∠EAD，∠AEF＝∠AED.‎ 又∵∠EAF＝15°，∴∠EAD＝15°，‎ ‎∴∠AED＝180°－90°－15°＝75°，‎ ‎∴∠AEF＝75°，‎ ‎∴∠FEC＝180°－75°－75°＝30°.‎ ‎[素养提升]‎ ‎[导学号：90702253]‎ 解：(1)∵△ADC≌△AFB，‎ ‎∴∠DAC＝∠FAB，‎ ‎∴∠DAC－∠BAC＝∠FAB－∠BAC，‎ ‎∴∠FAC＝∠DAB＝20°.‎ ‎(2)AF∥DC.‎ 理由：∵DA∥BF，‎ ‎∴∠DAF＋∠F＝180°.‎ ‎∵△ADC≌△AFB，∴∠D＝∠F，‎ ‎∴∠DAF＋∠D＝180°，∴AF∥DC.‎ ‎(3)∵AF∥DC，∴∠F＝∠FEC＝110°.‎ ‎∵AD∥BF，‎ ‎∴∠DAF＋∠F＝180°，‎ ‎∴∠DAF＝180°－110°＝70°，‎ ‎∴∠BAC＝∠DAF－∠DAB－∠FAC＝70°－20°－20°＝30°.‎ 6‎