八上时 轴对称二

八上时 轴对称二

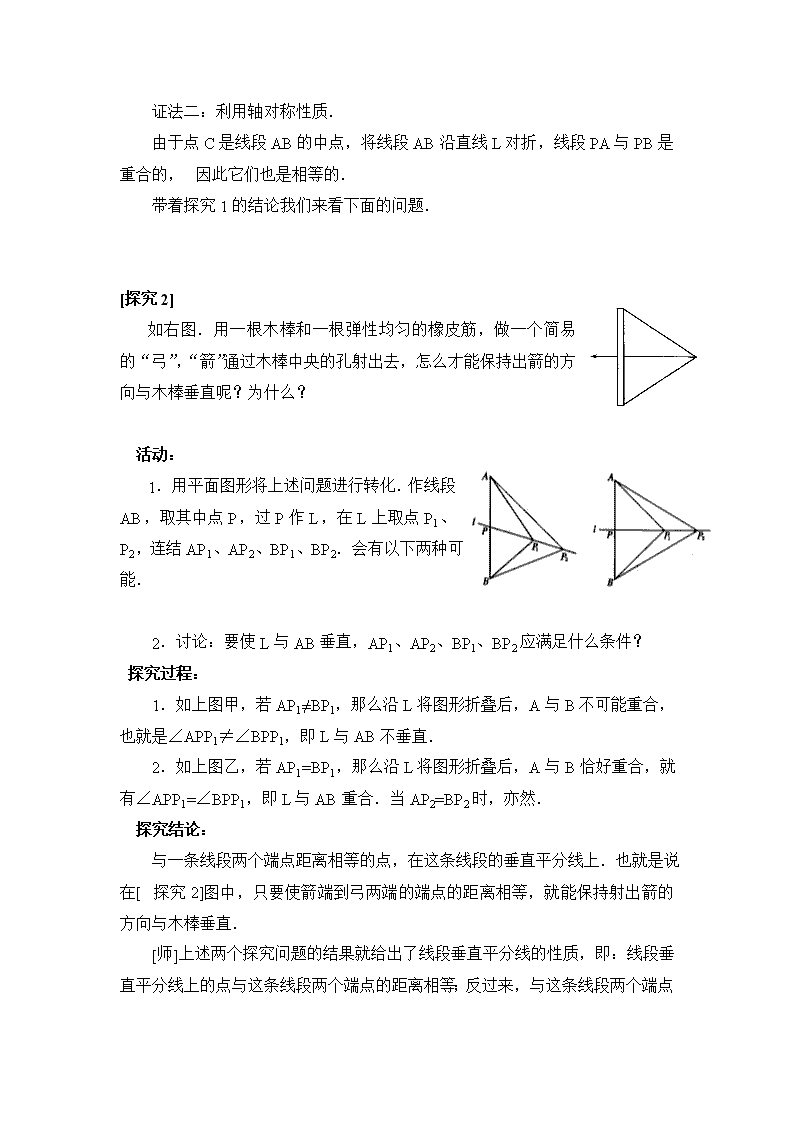
‎§14．1．2 轴对称（二）‎ ‎ 教学目标 ‎ 1．了解两个图形成轴对称性的性质，了解轴对称图形的性质．‎ ‎ 2．探究线段垂直平分线的性质．‎ ‎ 3．经历探索轴对称图形性质的过程，进一步体验轴对称的特点，发展空间观察．‎ ‎ 教学重点 ‎ 1．轴对称的性质．‎ ‎ 2．线段垂直平分线的性质．‎ ‎ 教学难点 ‎ 体验轴对称的特征．‎ ‎ 教学过程 ‎ Ⅰ．创设情境，引入新课 ‎ 上节课我们共同探讨了轴对称图形，知道现实生活中由于有轴对称图形，而使得世界非常美丽．那么大家想一想，什么样的图形是轴对称图形呢？‎ ‎ 今天继续来研究轴对称的性质．‎ ‎ Ⅱ．导入新课 观看投影并思考．‎ ‎ 如图，△ABC和△A′B′C′关于直线MN对称，点A′、B′、C′分别是点A、B、C的对称点，线段AA′、BB′、CC′与直线MN有什么关系？‎ ‎ 图中A、A′是对称点，AA′与MN垂直，BB′和CC′也与MN垂直．‎ ‎ AA′、BB′和CC′与MN除了垂直以外还有什么关系吗？‎ ‎ △ABC与△A′B′C′关于直线MN对称，点A′、B′、C′分别是点A、B、C的对称点，设AA′交对称轴MN于点P，将△ABC和△A′B′C′沿MN对折后，点A与A′重合，于是有AP=A′P，∠MPA=∠MPA′=90°．所以AA′、BB′和CC′与MN除了垂直以外，MN还经过线段AA′、BB′和CC′的中点．‎ ‎ 对称轴所在直线经过对称点所连线段的中点，并且垂直于这条线段．我们把经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线．‎ ‎ 自己动手画一个轴对称图形，并找出两对称点，看一下对称轴和两对称点连线的关系．‎ ‎ 我们可以看出轴对称图形与两个图形关于直线对称一样，对称轴所在直线经过对称点所连线段的中点，并且垂直于这条线段．‎ ‎ 归纳图形轴对称的性质：‎ ‎ 如果两个图形关于某条直线对称，那么对称轴是任何一对对称点所连线段的垂直平分线．类似地，轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线．‎ ‎ 下面我们来探究线段垂直平分线的性质．‎ ‎ [探究1]‎ 如下图．木条L与AB钉在一起，L垂直平分AB，P1，P2，P3，…是L上的点，分别量一量点P1，P2，P3，…到A与B的距离，你有什么发现？‎ ‎ 1．用平面图将上述问题进行转化，先作出线段AB，过AB中点作AB的垂直平分线L，在L上取P1、P2、P3…，连结AP1、AP2、BP1、BP2、CP1、CP2…‎ ‎ 2．作好图后，用直尺量出AP1、AP2、BP1、BP2、CP1、CP2…讨论发现什么样的规律．‎ ‎ 探究结果：‎ ‎ 线段垂直平分线上的点与这条线段两个端点的距离相等．即AP1=BP1，AP2=BP2，…‎ ‎ 证明．‎ ‎ 证法一：利用判定两个三角形全等．‎ ‎ 如下图，在△APC和△BPC中，‎ ‎ ‎ ‎ △APC≌△BPC PA=PB.‎ ‎ 证法二：利用轴对称性质．‎ ‎ 由于点C是线段AB的中点，将线段AB沿直线L对折，线段PA与PB是重合的，因此它们也是相等的．‎ ‎ 带着探究1的结论我们来看下面的问题．‎ ‎ ‎ ‎[探究2]‎ 如右图．用一根木棒和一根弹性均匀的橡皮筋，做一个简易的“弓”，“箭”通过木棒中央的孔射出去，怎么才能保持出箭的方向与木棒垂直呢？为什么？‎ ‎ 活动：‎ ‎1．用平面图形将上述问题进行转化．作线段AB，取其中点P，过P作L，在L上取点P1、P2，连结AP1、AP2、BP1、BP2．会有以下两种可能．‎ ‎ 2．讨论：要使L与AB垂直，AP1、AP2、BP1、BP2应满足什么条件？‎ ‎ 探究过程：‎ ‎ 1．如上图甲，若AP1≠BP1，那么沿L将图形折叠后，A与B不可能重合，也就是∠APP1≠∠BPP1，即L与AB不垂直．‎ ‎ 2．如上图乙，若AP1=BP1，那么沿L将图形折叠后，A与B恰好重合，就有∠APP1=∠BPP1，即L与AB重合．当AP2=BP2时，亦然．‎ ‎ 探究结论：‎ ‎ 与一条线段两个端点距离相等的点，在这条线段的垂直平分线上．也就是说在[探究2]图中，只要使箭端到弓两端的端点的距离相等，就能保持射出箭的方向与木棒垂直．‎ ‎ [师]‎ 上述两个探究问题的结果就给出了线段垂直平分线的性质，即：线段垂直平分线上的点与这条线段两个端点的距离相等；反过来，与这条线段两个端点距离相等的点都在它的垂直平分线上．所以线段的垂直平分线可以看成是与线段两端点距离相等的所有点的集合．‎ ‎ Ⅲ．随堂练习 课本P121练习 1、2．‎ ‎ Ⅳ．课时小结 ‎ 这节课通过探索轴对称图形对称性的过程，了解了线段的垂直平分线的有关性质，同学们应灵活运用这些性质来解决问题．‎ ‎ Ⅴ．课后作业 ‎ （一）课本习题14．1─3、4、9题．‎ ‎ 课后作业：＜＜课堂感悟与探究＞＞‎ Ⅵ．活动与探究 ‎ 如图甲，△ABC和△A′B′C′关于直线L对称，延长对应线段AB和A′B′，两条延长线相交吗？交点与对称轴L有什么关系？延长其他对应线段呢？在图乙中，AC与A′C′又如何呢？再找几个成轴对称的图形观察一下，能发现什么规律吗？‎ ‎ 过程：在图甲中，AB与A′B′不平行，所以它们肯定会相交．下面来研究交点与对称轴L的关系．‎ ‎ 问题1：点和直线有几种位置关系？‎ ‎ 有两种．一种是点不在直线上，另一种是点在直线上．‎ ‎ 问题2：先来假设一下交点不在对称轴L上，看是否成立．‎ ‎ 如果交点（P）不在对称轴L上，那么在L的另一侧一定有另外一点（P ‎′）与交点（P）关于直线L对称，且该点（P′）也是两延长线的交点．但是由于两条直线相交只可能有一个交点，所以这两点是重合的．即交点（P）只能在对称轴L上．所以交点一定在对称轴上．延长其他的对应线段，结果也一样．‎ ‎ 再看图乙，我们来讨论下一个问题．‎ ‎ AC与A′C′是平行的，它们的两条延长线也不会相交．‎ ‎ 结论：成轴对称的两个图形，对应线段的延长线如果相交，交点一定在对称轴上；对应线段的延长线如果不相交，也就是对应线段所在的直线平行，那么它们也与对称轴平行．‎ ‎ ‎ 板书设计 ‎ §14．1．2 轴对称（二）‎ ‎ 一、复习：轴对称图形．‎ ‎ 二、线段垂直平分线的定义：经过线段中点并且垂直于这条线段的直线，叫做线段的垂直平分线．‎ ‎ 三、图形轴对称的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对称点所连线段的垂直平分线．类似地，轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线．‎ ‎ 四、线段垂直平分线的性质：线段垂直平分线的点到这条线段两个端点的距离相等；反过来，与这条线段两个端点距离相等的点都在它的垂直平分线上．‎ ‎ ‎