等腰三角形导学案(1)

等腰三角形导学案(1)

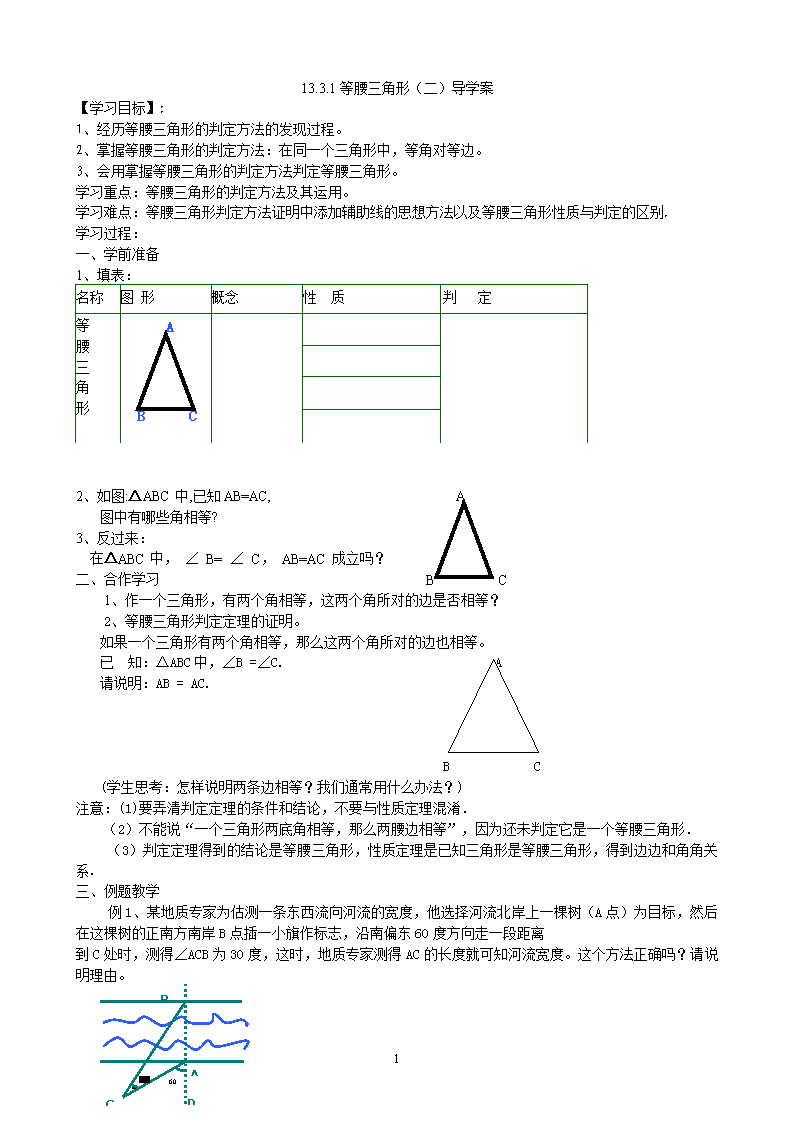
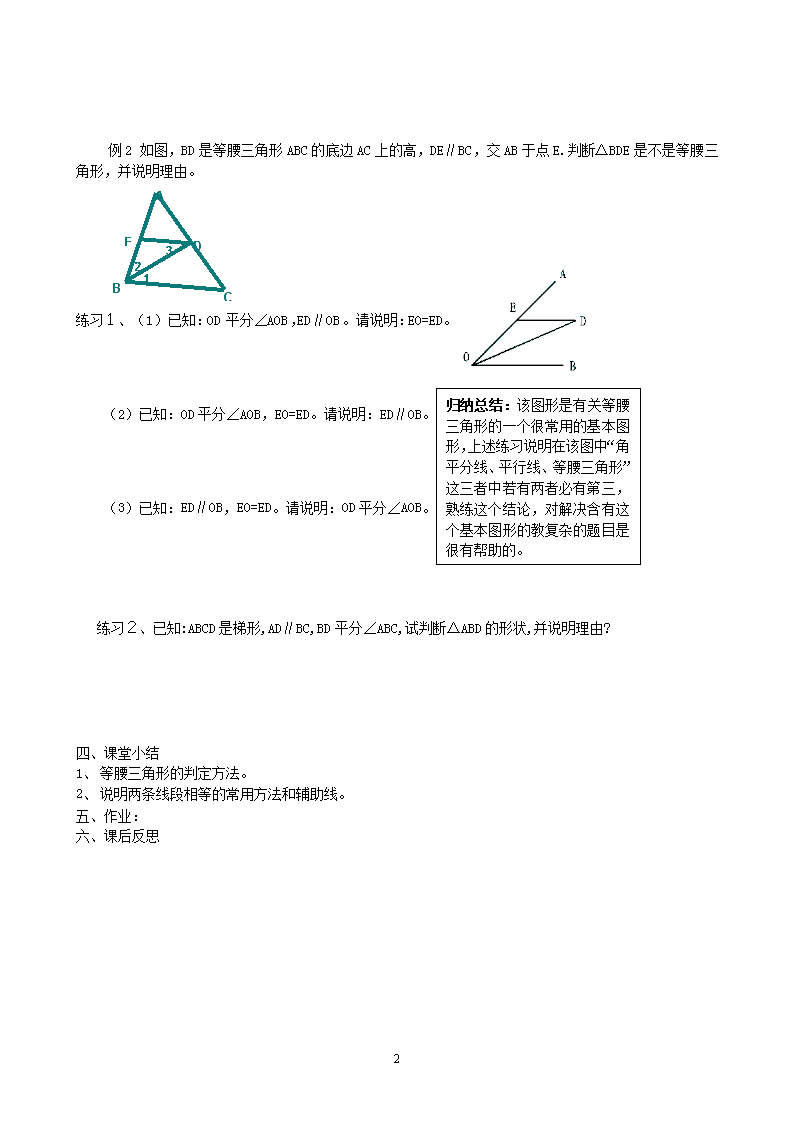
‎13.3.1等腰三角形（二）导学案 ‎【学习目标】:‎ ‎1、经历等腰三角形的判定方法的发现过程。‎ ‎2、掌握等腰三角形的判定方法：在同一个三角形中，等角对等边。‎ ‎3、会用掌握等腰三角形的判定方法判定等腰三角形。 ‎ 学习重点：等腰三角形的判定方法及其运用。‎ 学习难点：等腰三角形判定方法证明中添加辅助线的思想方法以及等腰三角形性质与判定的区别.‎ 学习过程：‎ 一、学前准备 ‎1、填表：‎ 名称 图 形 概念 性 质 ‎ 判 定 等 ‎ 腰 ‎ 三 ‎ 角 ‎ 形 ‎ ‎A B C ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎2、如图:ΔABC中,已知AB=AC, 　　　　A 图中有哪些角相等?‎ ‎3、反过来：‎ 在ΔABC中， ∠ B= ∠ C， AB=AC成立吗？‎ 二、合作学习 　　　　B C ‎ 1、作一个三角形，有两个角相等，这两个角所对的边是否相等？‎ ‎2、等腰三角形判定定理的证明。‎ 如果一个三角形有两个角相等，那么这两个角所对的边也相等。‎ 已　知：ΔABC中，∠B =∠C. 　　　　　　　　　　　 A 请说明：AB = AC.‎ ‎ 　　　 　　　　　　　 B C ‎(学生思考：怎样说明两条边相等？我们通常用什么办法？)‎ 注意：(1)要弄清判定定理的条件和结论，不要与性质定理混淆．‎ ‎　　（2）不能说“一个三角形两底角相等，那么两腰边相等”，因为还未判定它是一个等腰三角形．‎ ‎（3）判定定理得到的结论是等腰三角形，性质定理是已知三角形是等腰三角形，得到边边和角角关系. ‎ 三、例题教学 例1、某地质专家为估测一条东西流向河流的宽度，他选择河流北岸上一棵树（A点）为目标，然后在这棵树的正南方南岸B点插一小旗作标志，沿南偏东60度方向走一段距离 到C处时，测得∠ACB为30度，这时，地质专家测得AC的长度就可知河流宽度。这个方法正确吗？请说明理由。‎ B C A D 2‎ 例2 如图，BD是等腰三角形ABC的底边AC上的高，DE∥BC，交AB于点E.判断ΔBDE是不是等腰三角形，并说明理由。‎ A B C D E ‎1‎ ‎2‎ ‎3‎ 练习１、（1）已知：OD平分∠AOB，ED∥OB。请说明：EO=ED。‎ 归纳总结：该图形是有关等腰三角形的一个很常用的基本图形，上述练习说明在该图中“角平分线、平行线、等腰三角形”这三者中若有两者必有第三，熟练这个结论，对解决含有这个基本图形的教复杂的题目是很有帮助的。‎ ‎（2）已知：OD平分∠AOB，EO=ED。请说明：ED∥OB。‎ ‎（3）已知：ED∥OB，EO=ED。请说明：OD平分∠AOB。‎ ‎ 练习２、已知:ABCD是梯形,AD∥BC,BD平分∠ABC,试判断△ABD的形状,并说明理由?‎ 四、课堂小结 1、 等腰三角形的判定方法。‎ 2、 说明两条线段相等的常用方法和辅助线。‎ 五、作业：‎ 六、课后反思 2‎