八年级下数学课件：18-2-3 正方形 （共23张PPT）_人教新课标

八年级下数学课件：18-2-3 正方形 （共23张PPT）_人教新课标

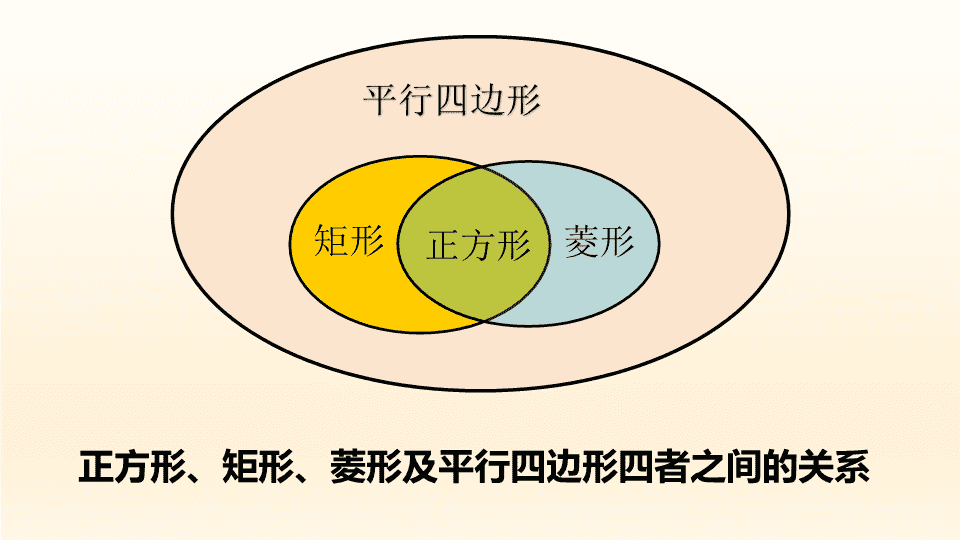
平行四边形 一个角是直角 矩形 菱形 一组邻边相等 平行四边形 探 究 新 知 1．矩形具有而菱形不具有的性质是( ) A．两组对边分别平行 B．对角线相等 C．对角线互相平分 D．两组对角分别相等 B 正方形、矩形、菱形及平行四边形四者之间的关系 矩形 菱形正方形 18.2　特殊的平行四边形 18.2.3正方形 正方形：有一个角是直角且一组邻边相等的平行四边形 一个角是直角 正方形 一组邻边相等 平行四边形 正方形 一个角是直角 菱形 正方形 一组邻边相等 矩形 正方形的性质 正方形的 两条对角线互相平分 垂直且相等,每条对角线平分一 组对角 正方形的对边平行 四边相等 正方形的四个角都是直角 边 对角线 角 A B C D O 二、正方形的性质 正方形的四个角都是直角，四条边都相等 正方形的两条对角线相等，并且互相垂直平分、 每条对角线平分一组对角 A B C D O 想一想 已知：四边形ABCD是正方形，对角线 AC、BD 相交于点O． 求证：△ABO、△BCO、△CDO、 △DAO是全等的等腰直角三角形． A B C D O 性质对比 边 角 对角线 平行四边形 矩形 菱形 正方形 对边平行且相等 对角相等 邻角互补 两条对角线互相平分 对边平行且相等 四个角都是直角 两条对角线平分且相 等 四条边都相等 对角相等邻角互补 两条对角线相互平分 垂直，且每条对角线 平分一组对角 四条边都相等 四个角都是直角 两条对角线相互平分 垂直且相等，且每条 对角线平分一组对角 练习题 1、周长为20cm的正方形,边长是 对角线长是 面 积是 。 2、正方形两条对角线的和为8cm，它的面积为____________. 3、正方形具有而矩形不一定有的性质是( ) A.四个角是直角 B.对角线互相垂直 C.对角线互相平分 D.对角线相等 4.矩形,菱形,正方形都具有的性质是( ) A.邻边相等 B. 邻角相等 C.对边相等 D. 对角互补 B 5√2 25 8 5 C 5.[反思] 判断以下命题的对错： 1．矩形的对角线相等且互相平分． (　　) 2．矩形的对角线相等且互相垂直． (　　) 3．菱形的对角线相等且互相平分． (　　) 4．菱形的对角线互相垂直且平分． (　　) 5．正方形的对角线相等且互相平分． (　　) 6．正方形的对角线互相垂直且平分． (　　) 7．正方形的对角线相等且互相垂直平分． (　　) √ × × √ √ √ √ 7.如图，E为正方形ABCD内一点，且△EBC是等 边三角形，求∠ECD与∠EAD的度数． 1．操作：将一张矩形纸片沿图18－2－30中所示的 箭头方向折叠，然后沿虚线剪开，所得的四边形ABCD是 ___________． 图18－2－30 正方形 正方形 平行四边形 一个角是直角 一组邻边相等 一组邻边相等 一个角是直角 菱形 矩形 n 1如图，将一张长方形纸片对折两次，然后剪下一个角，打开．如果要剪出一个正方形，那么 剪口线与折痕成（ ） n A．22.5°角B．30°角 C．45°角 D．60°角 n 2．下列判断中，正确的是(　　) n A．四边相等的四边形是正方形 n B．四角相等的四边形是正方形 n C．对角线互相垂直的平行四边形是正方形 n D．对角线互相垂直平分且相等的四边形是正方形 C D 例3如图，已知平行四边形ABCD中，对角线AC，BD相交于点 O，E是BD延长线上的点，且△ACE是等边三角形． (1)求证：四边形ABCD是菱形； (2)若∠AED＝2∠EAD，求证：四边形ABCD是正方形． n 如图，E，F，M，N分别是正方形ABCD四条边上的点，且AE＝BF＝CM＝DN.试判断四边形 EFMN是什么图形，并证明你的结论． 答案：四边形EFMN是正方形． 证明：∵四边形ABCD是正方形， ∴AB＝BC＝CD＝DA. 又∵AE＝BF＝CM＝DN， ∴AN＝DM＝CF＝BE. 由勾股定理可得EF＝FM＝MN＝EN. 易证△NAE≌△EBF，∴∠ANE＝∠BEF. ∵∠ANE＋∠AEN＝90°， ∴∠BEF＋∠AEN＝90°，∴∠NEF＝90°. ∴四边形EFMN是正方形． 一、正方形的定义 正方形：有一组邻边相等并且有一个角是直角的平行四边形是正方 形。 ①、正方形既是邻边相等的特殊矩形，又是有一个角是直角的特殊 菱形。 ②、正方形既具有矩形的性质有具有菱形的性质。 平行四边形 矩 形 菱 形 正 方 形 完全正方形 完全正方形，就是用一些大小不等的正方形，拼出来的一个大正方形．有 人可能以为，作出一个完全正方形是一件十分容易的事．其实不然，直到 本世纪30年代，还没有人能够作出一个完全正方形呢！当时，有些数学家 甚至断言，完全正方形是根本不存在的．半个多世纪之前，英国剑桥大学 有4个年轻的学生，．他们在理论的指导下，终于发现了一个由39个小正方 形组成的完全正方形．1976年，他们又在电子计算机的帮助下，又发现了 一个由21个小正方形组成的完全正方形(如图)． （图中的数字表示各个小正方形的边长） （图中的数字表示各个小正方形的边长） 17 19