《同步课时卷》北师版八年级数学（下册）1

《同步课时卷》北师版八年级数学（下册）1

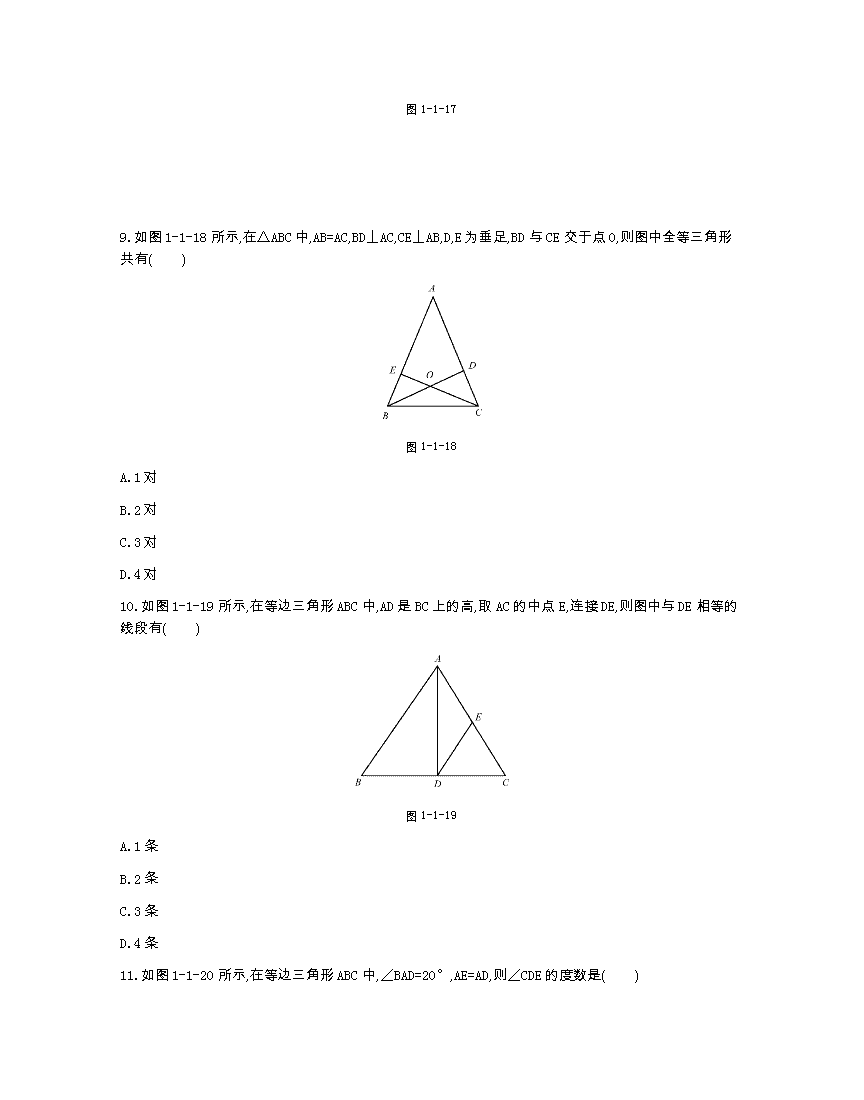
‎《同步课时卷》北师版八年级数学（下册）‎ ‎1.1等腰三角形（第二课时）‎ ‎1.“三线合一”是指等腰三角形顶角的平分线、底边上的　　、　　互相重合. ‎ ‎2.等边三角形的三个内角都　　,并且每个角都等于60°. ‎ ‎3.如图1-1-12所示,在△ABC中,已知AB=AC,BE,CD分别是∠ABC,∠ACB的角平分线,下列结论:①∠ABE=∠ACD;②BE=CD;③CD⊥AB,BE⊥AC.其中正确的是(　　)‎ 图1-1-12‎ A.①③‎ B.①②③‎ C.①②‎ D.②③‎ ‎4.如图1-1-13所示,在△ABC中,AB=AC,BD,CE为△ABC的两腰AC,AB上的中线,则图中全等三角形有(　　)‎ 图1-1-13‎ A.0对 B.1对 C.2对 D.3对 ‎5.如图1-1-14所示,AC=CD=DA=BC=DE,则∠BAE的度数为(　　)‎ 图1-1-14‎ A.100°‎ B.110°‎ C.120°‎ D.150°‎ ‎6.如图1-1-15所示,O为等边三角形ABC内一点,∠OCB=∠ABO,则∠BOC的度数是　. ‎ ‎　图1-1-15‎ ‎7.如图1-1-16所示,在△ABC中,AB=AC,AD⊥BC,D为垂足,点E,F分别是AC,AB上的点,要使DF=DE,则需要补充的条件是　　. ‎ 图1-1-16‎ ‎8.如图1-1-17所示,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE.求证:AD=CE.‎ 图1-1-17‎ ‎9.如图1-1-18所示,在△ABC中,AB=AC,BD⊥AC,CE⊥AB,D,E为垂足,BD与CE交于点O,则图中全等三角形共有(　　)‎ 图1-1-18‎ A.1对 B.2对 C.3对 D.4对 ‎10.如图1-1-19所示,在等边三角形ABC中,AD是BC上的高,取AC的中点E,连接DE,则图中与DE相等的线段有(　　)‎ 图1-1-19‎ A.1条 B.2条 C.3条 D.4条 ‎11.如图1-1-20所示,在等边三角形ABC中,∠BAD=20°,AE=AD,则∠CDE的度数是(　　)‎ 图1-1-20‎ A.10°‎ B.12.5°‎ C.15°‎ D.20°‎ ‎12.如图1-1-21所示,点D,E分别在等边三角形ABC的边BC,AC上,且BD=CE,连接AD,BE相交于点P,求∠APE的度数.‎ 图1-1-21‎ ‎13.已知:如图1-1-22所示,在△ABC中,AB=AC,AD=AE,BE,CD交于点O.求证:DO=EO.‎ 图1-1-22‎ 参考答案 ‎1.中线、高线 ‎2.相等 ‎3.C ‎4.D ‎5.C ‎6.120°‎ ‎7.DF⊥AB,DE⊥AC或BF=CE或AF=AE(答案不唯一)‎ ‎8.证明:∵△ABC为等边三角形,‎ ‎∴CA=AB,∠CAE=∠ABD,‎ 在△CAE和△ABD中,‎ ‎∴△CAE≌△ABD(SAS).‎ ‎∴AD=CE.‎ ‎9.C ‎10.D ‎11.A ‎12.解:∵△ABC是等边三角形,‎ ‎∴AB=BC,∠ABD=∠C=60°.‎ 又∵BD=CE,‎ ‎∴△ABD≌△BCE(SAS),‎ ‎∴∠BAD=∠CBE.‎ ‎∵∠APE=∠ABP+∠BAD,‎ ‎∴∠APE=∠ABP+∠CBE=∠ABC=60°.‎ ‎13.证明:∵AB=AC,AD=AE,‎ 又∵∠A=∠A,‎ ‎∴△AEB≌△ADC,‎ ‎∴∠1=∠2.‎ ‎∵BD=AB-AD,CE=AC-AE,‎ ‎∴BD=CE.‎ 又∵∠BOD=∠COE,‎ ‎∴△BOD≌△COE,‎ ‎∴DO=EO.‎