- 2021-11-01 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版数学九年级上册期末复习拓展
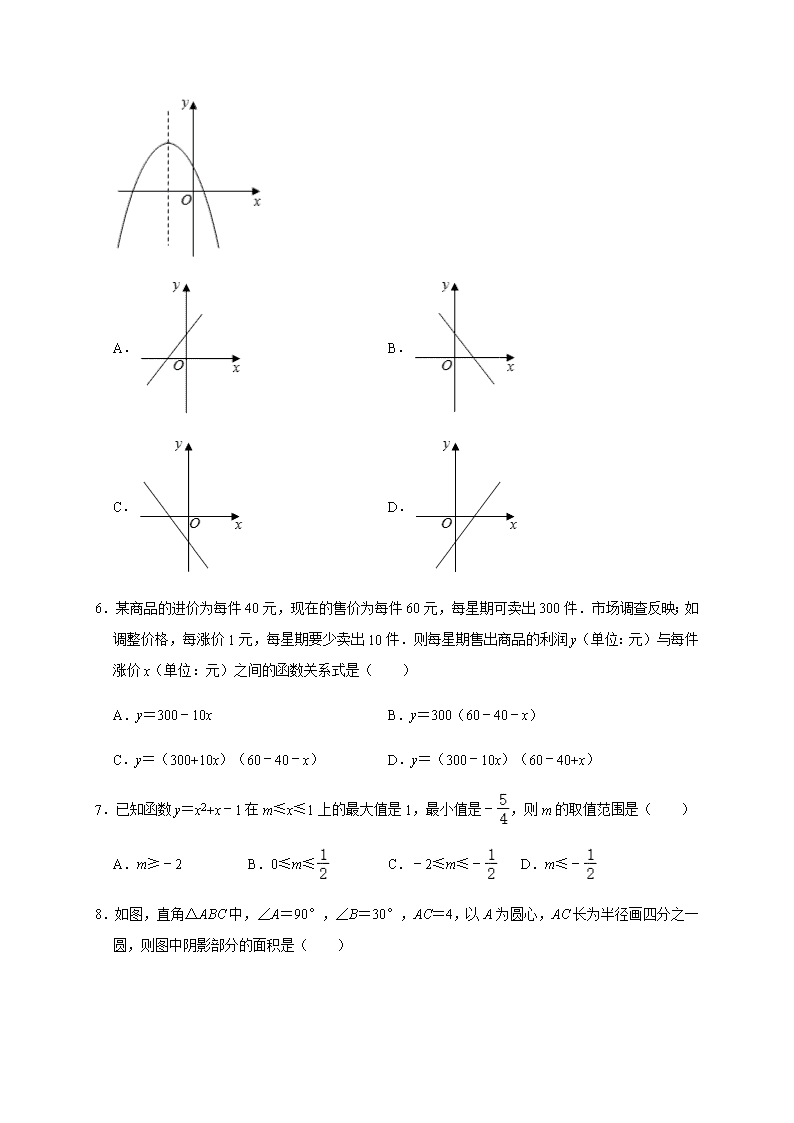
人教版数学九年级上册期末复习拓展 一.选择题 1.下列四个圆形图案中,既是轴对称图形,又是中心对称图形的是( ) A. B. C. D. 2.若一个圆内接正多边形的内角是 108°,则这个多边形是( ) A.正五边形 B.正六边形 C.正八边形 D.正十边形 3.用配方法解一元二次方程 x2﹣9x+19=0,配方后的方程为( ) A.(x﹣ )2= B.(x+ )2= C.(x﹣9)2=62 D.(x+9)2=62 4.某小区 2018 年屋顶绿化面积为 2000m2,计划 2020 年屋顶绿化面积要达到 2880m2.设该小区 2018 年至 2020 年屋顶绿化面积的年平均增长率为 x,则可列方程为( ) A.2000(1+2x)=2880 B.2000×(1+x)=2880 C.2000+2000(1+x)+2000(1+x)2=2880 D.2000(1+x)2=2880 5.二次函数 y=ax2+bx+c 的图象如图所示,那么一次函数 y=ax+b 的图象大致是( ) A. B. C. D. 6.某商品的进价为每件 40 元,现在的售价为每件 60 元,每星期可卖出 300 件.市场调查反映;如 调整价格,每涨价 1 元,每星期要少卖出 10 件.则每星期售出商品的利润 y(单位:元)与每件 涨价 x(单位:元)之间的函数关系式是( ) A.y=300﹣10x B.y=300(60﹣40﹣x) C.y=(300+10x)(60﹣40﹣x) D.y=(300﹣10x)(60﹣40+x) 7.已知函数 y=x2+x﹣1 在 m≤x≤1 上的最大值是 1,最小值是﹣ ,则 m 的取值范围是( ) A.m≥﹣2 B.0≤m≤ C.﹣2≤m≤﹣ D.m≤﹣ 8.如图,直角△ABC 中,∠A=90°,∠B=30°,AC=4,以 A 为圆心,AC 长为半径画四分之一 圆,则图中阴影部分的面积是( ) A.4 ﹣ B.2 ﹣ C.4 + D.2 + 9.一只机器猫每秒钟前进或后退一步,程序设计人员让机器猫以每前进 3 步再后退 2 步的规律移动. 如果将机器猫开始放在数轴的原点上,面向正方向,以 1 步的距离作为 1 个单位长,令 P(n)表 示第 n 秒时机器猫所在的位置的坐标.P(0)=0,那么下列结论中不正确的是( ) A.P(3)=3 B.P(5)=1 C.P(101)=21 D.P(103)<P(104) 10.已知 α 、 β 是方程 x2+2x﹣5=0 的两个实数根,则 α 2+ β 2+2 α +2 β 的值为( ) A.6 B.8 C.10 D.12 二.填空题 11.已知关于 x 的一元二次方程 x2+a2x+a﹣3=0 的一个根是 1,则 3a2+3a﹣4 的的值为 . 12.已知一元二次方程 x2﹣4x+3=0 的两根 x1、x2,则 2x12﹣8x1+x1x2= . 13.在平面直角坐标系中,点 A(﹣5,b)关于原点对称的点为 B(a,6),则(a+b)2019= . 14.如图,已知 ⊙ O 是以数轴上原点 O 为圆心,半径为 2 的圆,∠AOB=45°,点 P 在 x 正半轴上 运动,若过点 P 且与 OA 平行的直线与 ⊙ O 有公共点,设 P 点对应的数为 x,则 x 的取值范围 是 . 15.二次函数 的最大值是 . 三.解答题 16.解方程: (1)4x2﹣3x =18(用配方法); (2)(y﹣2)(3y﹣5)=1(用公式法); (3)2x2+4x=x+2(用适当的方法). 17.已知点(0,3)在二次函数 y=ax2+bx+c 的图象上,且当 x=1 时,函数 y 有最小值 2. (1)求这个二次函数的表达式. (2)如果两个不同的点 C(m,6),D(n,6)也在这个函数的图象上,求 m+n 的值. 18.在绵阳市乡村振兴政策的帮扶下,某农户欲通过电商平台销售自家农产品,已知这种产品的成 本价为 10 元/千克.市场调查发现,该产品每天的销售量 w(千克)与销售价 x(元/千克)大致有如 下关系:w=﹣4x+80.设这种产品每天的销售利润为 y(元). (1)当销售价定为多少元时,每天的销售利润最大?最大利润是多少? (2)如果物价部门规定这种产品的销售价不得高于 20 元/千克,该农户想要每天获得 84 元的销 售利润,销售价应定为多少元? 19.如图,已知平行四边形 ABCD 中,AE⊥BC 于点 E,以点 B 为中心,取旋转角等于∠ABC,把 △BAE 顺时针旋转,得到△BA′E′,连接 DA′.若∠ADC=60°,∠ADA′=50°. (Ⅰ)求∠DA′E′的大小; (Ⅱ)若延长 AE 和 A′E′相交于点 P,求∠APA′的大小? (Ⅲ)连接 PB,若 AB=a,求 PB 的长度. 20.如图,△ABC 内接于 ⊙ O,AB 是 ⊙ O 的直径,C 是 中点,弦 CE⊥AB 于点 H,连结 AD, 分别交 CE、BC 于点 P、Q,连结 BD. (1)求证:P 是线段 AQ 的中点; (2)若 ⊙ O 的半径为 5,D 是 的中点,求弦 CE 的长.查看更多