- 2021-11-01 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件《探索三角形全等的条件》 (10)_苏科版
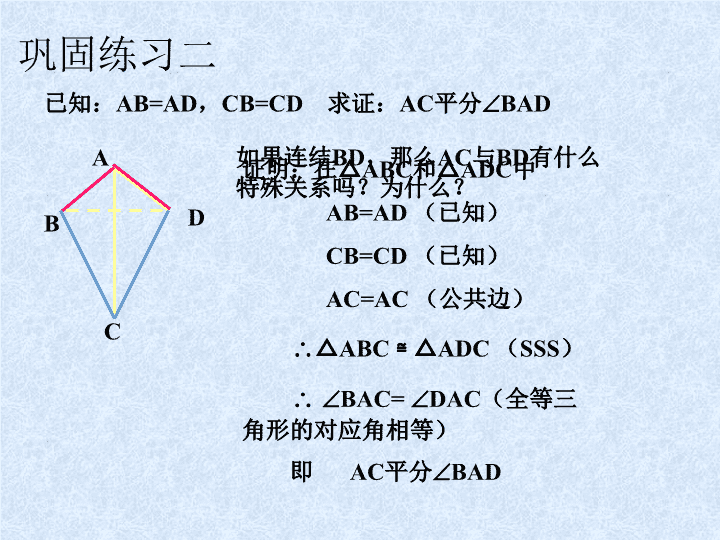
初中数学八年级上册 (苏科版) 探索三角形全等的条件 (四) 判断 (1)判断两个三角形全等的条件中,至少 要有一个角对应相等。 ( ) (2)有一组边对应相等的两个等边三角形 全等 。 ( ) (3)两腰对应相等的两个三角形全等。 ( ) (4)底边和腰对应相等的两个等腰三角形 全等。( ) 巩固练习一 巩固练习二 已知:AB=AD,CB=CD 求证:AC平分BAD A B C D 证明:在△ABC和△ADC中 AB=AD (已知) CB=CD (已知) AC=AC (公共边) △ABC ≌ △ADC (SSS) BAC= DAC(全等三 角形的对应角相等) 即 AC平分BAD 如果连结BD,那么AC与BD有什么 特殊关系吗?为什么? C B A D 情境1: 小时候,我们都折过纸飞机,它的翼面如图形状,你能 说出它的特征吗?这样做有什么好处? 情境2: 工人师傅常常利用角尺平分一个任意角,如图,在COD的 两边OC,OD上分别任取OA=OB,移动角尺,使角尺两边相同 的刻度分别与点A,B重合,这时过角尺顶点M的射线OM就 是COD的平分线。 O A B M D C 你能说明射线OC是∠AOB的平分线 的道理吗? 已知:点C、F在AD上,AF=DC,AB=DE,BC=EF 求证: A= D A B C D E F 例题 如图,AD=BE,OD=OE,∠1=130º,∠2=25º.根据上 面的条件,你能得到哪些结论呢? 说出你的理由. 21 E O BA D 变化:在题中,如果删去“∠1=130º,∠2=25º”的条件, 要使△DOA≌EOB,你认为还可以添加一个什么条件? 练一练 小明在学习上非常爱动脑筋,一次,他想出了另一种用尺规 平分一个任意角的方法.如图,以∠AOB的顶点O为圆心,分别以 1cm和3cm长为半径画弧,两弧分别与角的两边OA、OB交于点D1、E1 和D2、E2,连结D1E2和D2E1,交点为C,作射线OC,则射线OC就是 ∠AOB的平分线.你能说出他这样作的理由吗? A B E1 E2O D1 C D2 练一练 已知:在△ABC中,AB=AC,D是BC的中点。 求证: ADBC A B C D 练一练 证明: ∵ D是BC的中点(已知) BD=CD(线段中点的定义) 在△ADB 和△ADC中 AB=AC, BD=CD ,AD=AD △ADB ≌ △ADC(SSS) ∵ ADB= ADC(全等三角形对应角相等) 又∵ ADB与 ADC是邻补角 ADB= ADC=90° ADBC(垂直的定义) 小结 1、会用直尺和圆规作角平分线 2、能有条理地说理和表达 作业布置查看更多