- 2021-11-01 发布 |
- 37.5 KB |
- 16页


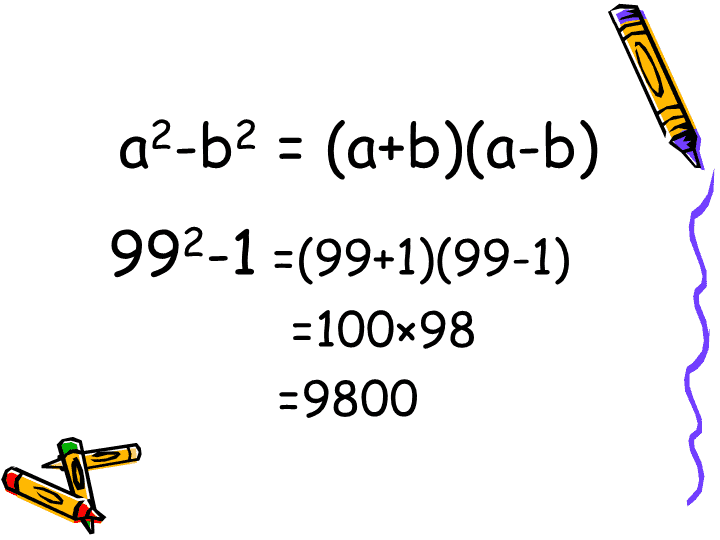
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下数学课件八年级下册数学课件《因式分解》 北师大版 (9)_北师大版
992-1 a2-b2 = (a+b)(a-b) 992-1 =(99+1)(99-1) =100×98 =9800 学习目标 • 1、理解因式分解的意义和概念; • 2、认识因式分解与整式乘法的相互关 系——互逆关系。 • 3、能利用因式分解解决相关的问题。 当我们需要确定一个代数式能否 被一个整数整除时,有哪些方法? 将代数式化成积的形式,若其 中含有该整数,则可被整除; 反之,则不能被整除。 a3-a=a(a+1)(a-1) 单项式×多项式×多项式 ma+mb+mc=m(a+b+c) 单项式×多项式 X2+2x+1=(x+1)2 多项式×多项式 整 式 × 整 式 多 项 式 因式分解的概念: • 把一个多项式化成几个整式的积的 形式,这种变形叫做因式分解,也 可称为分解因式。 (1)2ax-2ay=2a(x-y) (2) a 2-b2+1=( a +b)( a -b)+1 (3)4x2-8x-1=4x(x-2)-1 (4)a2-4=(a+2)(a-2) (5)6x2y3=3xy·2xy2 (6) 2 2 1 1 1x x xx xx 判断变形是因式分解应满足哪些条件? ma+mb+mc m(a+b+c) 整式的乘法与因式分解是 互逆关系 分解因式 整式乘法 B • 某多项式分解因式的结果为 (x+2y)(x-2y),那么这个 多项式是( ) A、4x2-y2 B、x2-4y2 C、4x2+y2 D、x2+4y2 当我们需要确定自己分解因式的结 果是否正确时,可以怎么做? 将结果进行整式乘法的运算, 看与该多项式是否一致,一致 则正确,不一致则错误 • 课堂检测: • 下列各式从左到右的变形,( )是因式分解, ( ) 是整式的乘法。 • (1)4a(a+2b)=4a2+8ab • (2)6ax-3ax2=3ax(2-x) • (3)3a2x-6bx+3x=3x(a2-2b) • (4)x2-3x+2=x(x-3)+2 • (5)36a2b=3a·12ab • (6) x abxabx 2 1 归纳小结 2.分解因式与整式乘法是互逆过程 3.分解因式要注意的问题: (1) 分解的对象必须是多项式 (2) 分解的结果必须是几个整式的 乘积的形式 (3) 要分解到不能再分解为止 1.分解因式的概念 • 23-2=2×3×1 • 993-9 =99×100×98 • 1013-101=101×102×100 • a3-a =a(a+1) ×(a-1) • 体现了“从特殊到一般”的 数学思想 • 运用了“类比”的数学方法查看更多