八年级数学上册第2章三角形2-5全等三角形第4课时角角边AAS课件 湘教版

八年级数学上册第2章三角形2-5全等三角形第4课时角角边AAS课件 湘教版

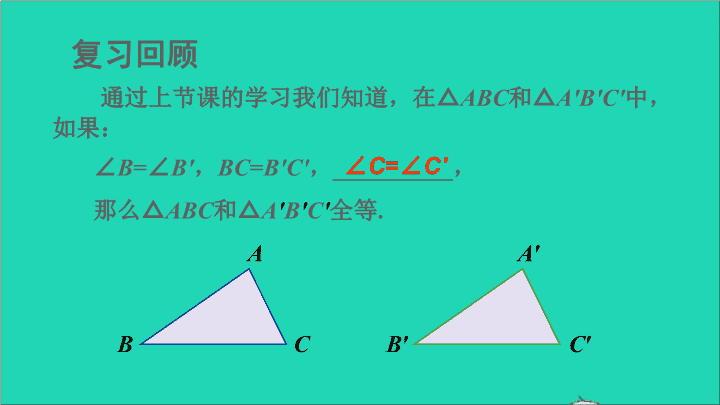
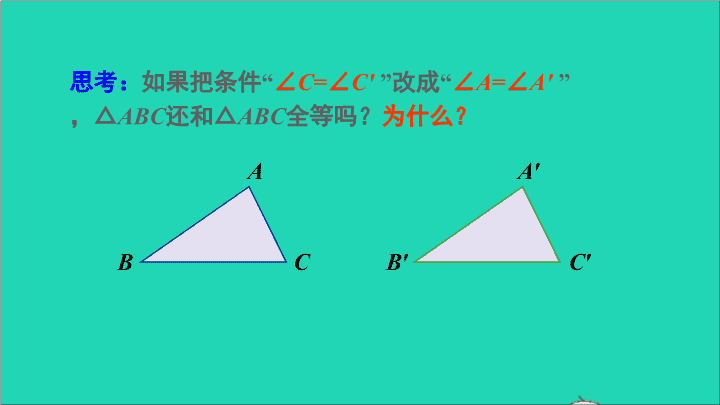
第4课时 角角边（AAS） 2 复习回顾 通过上节课的学习我们知道，在△ABC和△A′B′C′中， 如果： ∠B=∠B′，BC=B′C′，__________， 那么△ABC和△A′B′C′全等. ∠C=∠C′ A′ B′ C′ A B C 思考：如果把条件“∠C=∠C′ ”改成“∠A=∠A′ ”， △ABC还和△ABC全等吗？为什么？ A′ B′ C′ A B C 动脑筋 推进新课 如图，在△ABC和△A′B′C′中，如果∠A=∠A′，∠B=∠B′， BC=B′C′， 那么△ABC和△A′B′C′全等吗？ A′ B′ C′ A B C 证明 在△ABC和△A′B′C′中， ∵ ∠A =∠A′， ∠B =∠B′， ∴ ∠C =∠C′. 又∵ BC=B′C′， ∠B=∠B′， ∴ △ABC ≌ △A′B′C′(ASA). 分析： △ABC≌ △A′B′C′. 根据三角形内角和 定理，可将上述条 件 转 化 为 满 足 “ASA”的条件. 结论 由此得到判定两个三角形全等的定理： 两角分别相等且其中一组等角的对边相 等的两个三角形全等. (可简写成“角角边”或“AAS”). 角角边定理 　　归纳概括“AAS”判定方法： 两角分别相等且其中一组等角的对边相等的两个三 角形全等（简写为“角角边”或“AAS”）． 几何语言： 在△ABC 和△ A′B′ C′中， ∠B =∠B′， ∠C =∠C′， AB = A′B′， A B C || ||| | A′ B′ C′ || ||| | 已知：如图，∠B=∠D，∠1=∠2. 求证：△ABC≌ △ADC. 例5 证明 ∵∠1=∠2， ∴∠ACB=∠ACD（等角的补角相等）. 在△ABC和△ADC中， ∠B = ∠D， AC = AC， ∠ACB = ∠ACD， 例6 已知：如图，点B，F，C，E在同一条直线上， AC∥FD，∠A=∠D，BF=EC. 求证：△ABC≌ △DEF. 证明 ∵ AC∥FD ， ∴∠ACB=∠DEF ， ∵ BF=EC ， ∴ BF+FC=EC+FC ， 即BC=EF. 例6 已知：如图，点B，F，C，E在同一条直线上， AC∥FD，∠A=∠D，BF=EC. 求证：△ABC≌ △DEF. 在△ABC和△DEF中， ∠A = ∠D， BC = EF， ∠ACB = ∠DEF， 练习 1. 已知：如图，∠1 =∠2，AD=AE. 求证：△ADC≌ △AEB. 证明 在△ADC和△AEB中， ∠1 = ∠2， AD = AE， ∠DAC = ∠EAB（公共角）， 2. 已知：在△ABC中，∠ABC=∠ACB，BD⊥AC于点D， CE⊥AB 于点E. 求证： BD=CE. 证明 ∵BD⊥AC ，CE⊥AB ， 在△BCE和△CBD中， ∠EBC = ∠DCB ， BC = CB， ∠CEB = ∠BDC ， 巩固练习 1.如图，在△ACD和△BDC中，∠A＝∠B，∠ACD＝∠BDC， 则证明这两个三角形全等最直接的方法是____________.“AAS” 2.如图，已知∠ABD＝∠CBD，若以“AAS”为依据判定 △ABD≌ △CBD，还需添加的一个条件是____________.∠A=∠C 3.如图，点A，D，C在同一条直线上，AB∥EC，AC＝CE， ∠B＝∠EDC. 求证：BC＝DE. 证明 ∵AB∥EC， 在△ABC和△CDE中， ∠B = ∠EDC ， AC = CE， ∠A = ∠DCE ， 4.如图所示，在△ABC中，∠B＝∠C，点D，E在边BC上， AD＝AE. （1）求证：△ABD≌ △ACE； （2）若∠ADE＝60°，AD＝6，BE＝8，求BD的长. （1）证明 ∵AD=AE，∴∠ADE=∠AED， ∴∠ADB=∠AEC. 在△ABD和△ACE中， ∠ADB = ∠AEC ， AD = AE， ∠B = ∠C ， （2）解：∵ ∠ADE＝60°，AD＝AE， ∴ △ADE为等边三角形. ∴ AD＝DE＝6 . ∴BD＝BE－DE＝8－6＝2. 课后小结 A B C || ||| | A′ B′ C′ || ||| | 两角分别相等且其中一组等角的对边相 等的两个三角形全等. (可简写成“角角边”或“AAS”).