- 2021-10-27 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
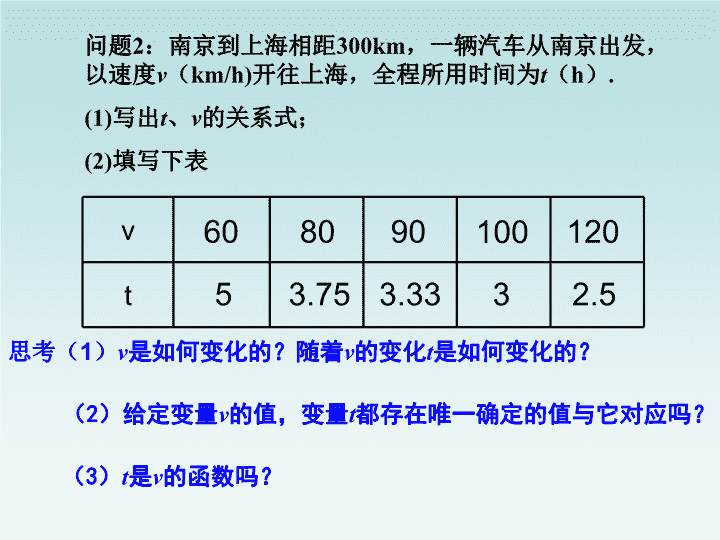
八年级下数学课件《反比例函数》 (7)_苏科版
初中数学八年级下册 (苏科版) 第11章 反比例函数 自主先学,预习展示 问题1:(1)复习反比例关系、函数的相关概念; (2)回顾我们学过的哪些函数; (3)举出这些函数的实例,列出函数表达式. v t 60 10080 90 120 问题2:南京到上海相距300km,一辆汽车从南京出发, 以速度v(km/h)开往上海,全程所用时间为t(h). (1)写出t、v的关系式; (2)填写下表 思考(1)v是如何变化的?随着v的变化t是如何变化的? (2)给定变量v的值,变量t都存在唯一确定的值与它对应吗? (3)t是v的函数吗? 5 3.75 3.33 3 2.5 实验展示 一个面积为12的矩形,长为x,宽为y. (1)写出x、y的关系式; (2)在工具板上构造面积为12的“格点”矩形,你 能构造出几个这样的“格点”矩形? B 一个单位长度 公共顶点 4×5的“格点”矩形 (1)随着长x的变化宽y是如何变化的? (2)给定变量x的值,变量y都存在唯一确定的值 与它对应吗? 思考: (3)y是x的函数吗? 用函数表达式表示下列问题中两个变量之间的关系: (1)一家银行为某社会福利厂提供20万元的无息贷 款,该厂的平均年还款额y (万元) 随还款年限x (年) 的变化而变化; (2)游泳池的容积为5000 m3,向池内注水,注满水 池所需时间t (h) 随注水速度v (m3/h) 的变化而变化; (3)实数m与n的积为-200,m随n的变化而变化. 讨论展示 探索概念 xy 2 1 13 xy1xy xy 7 2 012 xy x my 4 ① ③② ④ ⑤ ⑥ (m为常数) 例1:下列函数表达式中的y是x的反比例函数吗?如 果是,把它写成 的形式,并指出k的值. x ky 反比例函数不总是以一般形式出现,有时还会 以其他形式出现,但都可以转化为一般形式。 kxy x ky 1 kxy 例2:写出下列问题中两个变量之间关系的函数表达 式,并判断它们是否为反比例函数. (1)根据《徐州统计年鉴》资料显示,徐州市公园绿 地面积为2720公顷,人均公园绿地面积S(公顷/人)随 全市人口n(人)的变化而变化; (2)体积是100 cm3 的圆锥,高h (cm) 随底面面积S (cm2) 的变化而变化; 应用概念 反比例函数在生活中的应用是非常广泛的,仿照今天 所学,编写一道体现反比例函数关系的实际问题。 要求:每位同学出一题,小组讨论,每组选出一题 进行展示。 小组合作 交流展示 (1)建立适当的直角坐标系,将D1、D2、D3、D4、D5、D6的 坐标表示出来; (2)用一条平滑的曲线将D1、D2、D3、D4、D5、D6连起来; (3)取这条曲线上的任意一点,向x轴、y轴作垂线,猜想所形 成的矩形的面积是多少? xy 12 质 疑 拓 展 D6 D5 D4 D3 D2 D1 B 当堂检测 时间是个常数,但对勤奋者来说,是 个‘变数’.用‘分’来计算时间的人比 用‘小时’来计算时间的人时间多59倍. ----雷巴柯夫查看更多