八年级上数学课件八年级上册数学课件《平面直角坐标系》 北师大版 (2)_北师大版

八年级上数学课件八年级上册数学课件《平面直角坐标系》 北师大版 (2)_北师大版

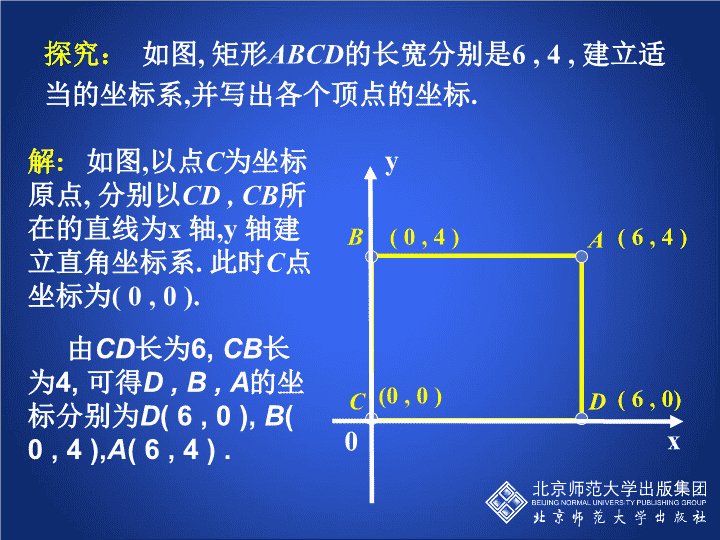
第三章 位置与坐标 2. 平面直角坐标系（第3课时） 探究： 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适 当的坐标系,并写出各个顶点的坐标. B C D A 解: 如图,以点C为坐标 原点, 分别以CD , CB所 在的直线为x 轴,y 轴建 立直角坐标系. 此时C点 坐标为( 0 , 0 ). x y 0 (0 , 0 ) ( 0 , 4 ) ( 6 , 4 ) ( 6 , 0) 由CD长为6, CB长 为4, 可得D , B , A的坐 标分别为D( 6 , 0 ), B( 0 , 4 ),A( 6 , 4 ) . 交流.在上面的问题中，你还可以怎样建立直角坐标系？ 与同伴交流. x y 0 x y 0 x y 0 x y 0 应用： 如图，正三角形ABC的边长为 6 , 建立适当的 直角坐标系 ,并写出各个顶点的坐标 . A B C 解: 如图,以边AB所在 的直线为x 轴,以边AB 的中垂线y 轴建立直角 坐标系. 由正三角形的性质可 知CO= ,正三角形 ABC各个顶点A , B , C的坐标分别为 A ( -3 , 0 );B ( 3 , 0 ); C ( 0 , ).3 3 3 3 y x0( -3 , 0 ) ( 3 , 0 ) ( 0 , )3 3 ６ ３ A B C y x 0 ( -3 , - ) ( 3 , - ) ( 0 , 0 ) 3 3 ６ ３ 交流.在上面的问题中，你还可以怎样建立直角坐标系？ 与同伴交流. 3 3 1、 如图，分别建立两个不同的直角坐标系，在各个 直角坐标系中，分别写出八角星 8 个角或四角星 4 个角的顶点的坐标，并比较同一顶点在两个坐标系中 的坐标． 2、如图，在一次军棋比赛中，如果团长所在的位置 的坐标为（2，－5），司令所在的位置的坐标为（4， －2），那么工兵所在的位置的坐标为 。 3.在一次“寻宝”游戏中，寻宝人已经找到了坐标为 （3，2）和（3，-2）的两个标志物A,B，并且知道藏 宝地点的坐标（4，4），除此外不知道其他信息。如 何确定直角坐标系找到“宝藏”？ 考考你 提示: 连接两个标志点, 作所得线段 的中垂线,并以这条线为横轴. 那如何来确定纵轴? 考考你 4、已知边长为2的正方形OABC在直角坐标系中（如 图）， OA与y轴的夹角为30°，那么点A的坐标 为 ，点C的坐标为 ，点B的坐标为 。 1. 坐标平面内的点与有序实数对是一一 对应的。 2. 给出坐标平面内的一点，可以用它所 在象限或坐标轴来描述这个点所在平 面内的位置。 3. 要记住各象限内点的坐标的符号，会根 据对称的知识找出已知点关于坐标轴或原 点的对称点。 小结： A类：课本习题3.4。 B类：完成A类同时，补充： （1）已知点A到x轴、y轴的距离均为4，求A点坐标； （2）已知x轴上一点A（3，0），B (3,b) ，且AB=5, 求b的值 。 C类：建立坐标系表示右面图形各顶点的坐标。 直角梯形上底3，下底5，底角60˚ o x y