八年级数学上册第六章数据的分析专题课堂七数据分析的实际应用课件新版北师大版

八年级数学上册第六章数据的分析专题课堂七数据分析的实际应用课件新版北师大版

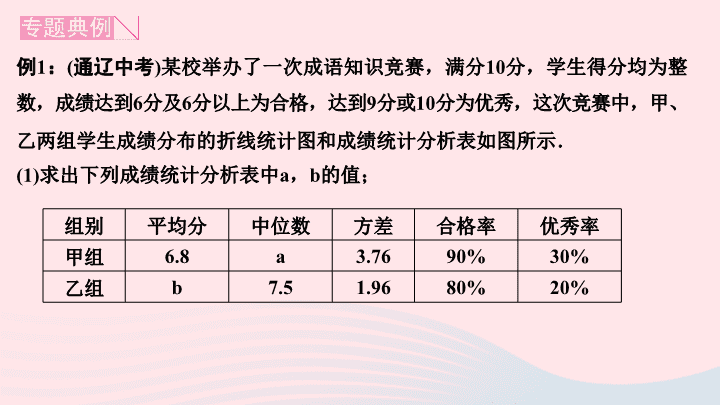
第六章　数据的分析 专题课堂(七)　数据分析的实际应用 例 1 ： ( 通辽中考 ) 某校举办了一次成语知识竞赛，满分 10 分，学生得分均为整数，成绩达到 6 分及 6 分以上为合格，达到 9 分或 10 分为优秀，这次竞赛中，甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示． (1) 求出下列成绩统计分析表中 a ， b 的值； 组别 平均分 中位数 方差 合格率 优秀率 甲组 6.8 a 3.76 90% 30% 乙组 b 7.5 1.96 80% 20% (2) 小英同学说： “ 这次竞赛我得了 7 分，在我们小组中排名属中偏上！ ” 观察上面表格判断，小英是甲、乙哪个组的学生； (3) 甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组，但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你写出两条支持乙组同学观点的理由． 分析： (1) 由折线图中数据 ， 根据中位数和加权平均数的定义求解可得； (2) 根据中位数的意义求解可得； (3) 可从平均数和方差两方面阐述即可． (2) 因为甲组的中位数为 6 ，乙组的中位数为 7.5 ， 而小英的成绩位于小组中上游，所以小英属于甲组学生 (3) ① 乙组的平均分高于甲组，即乙组的总体平均水平高； ② 乙组的方差比甲组小，即乙组的成绩比甲组的成绩稳定 1 ．甲、乙两人参加某体育项目训练， 近期的五次测试得分情况如图所示． (1) 分别求出两人得分的平均数与方差； (2) 根据图示和上面算得的结果， 对两人的训练成绩从如下几个方面进行评价： ①将平均数和方差相结合看； ②将平均数和中位数相结合看； ③将平均数和折线图走势结合看． (2)① 因为平均数相等， s 甲 2 >s 乙 2 ，所以乙的成绩较稳定 ②易知甲的中位数是 13 ，乙的中位数为 13. 因为中位数相同，平均数也相同，所以两人成绩相当 ③因为平均数相同，甲的成绩基本上呈上升状态，所以甲较有潜力 2 ．某学校对初中毕业班经过初步比较后，决定从九年级 (1)(4)(8) 班这三个班中推荐一个班作为市级先进班集体的候选班，现对这三个班进行综合素质考评，下表是这三个班五项素质考评的得分表 ( 单位：分，每项满分为 10 分 ). (1) 请问：各班五项考评分的平均数、中位数和众数中，哪个统计量不能反映三个班的考评结果的差异？ (2) 根据你对表中五个项目的重要程度的认识，设定一个各项考评内容的占分比例 ( 比例的各项需满足：①均为整数；②总和为 10 ；③不全相同 ) ，按这个比例对各班的得分重新计算，比较出大小关系，并从中推荐一个得分最高的班作为市级先进班集体的候选班． 例 2 ： ( 河南中考 ) 每到春夏交替时节，雌性杨树会以满天飞絮的方式来传播下一代，漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等，给人们造成困扰，为了解市民对治理杨絮方法的赞同情况，某课题小组随机调查了部分市民 ( 问卷调查表如表所示 ) ，并根据调查结果绘制了如下尚不完整的统计图． 治理杨絮 —— 您选哪一项？ ( 单选 ) A ．减少杨树新增面积，控制杨树每年的栽种量 B ．调整树种结构，逐渐更换现有杨树 C ．选育无絮杨品种，并推广种植 D ．对雌性杨树注射生物干扰素，避免产生飞絮 E ．其他 根据以上统计图，解答下列问题： (1) 本次接受调查的市民共有 2000 人； (2) 扇形统计图中，扇形 E 的圆心角度数是 28.8° ； (3) 请补全条形统计图； (4) 若该市约有 90 万人，请估计赞同 “ 选育无絮杨品种，并推广种植 ” 的人数． 3 ． (2019 · 荆门 ) 高尔基说： “ 书，是人类进步的阶梯． ” 阅读可以丰富知识、拓展视野、充实生活等诸多益处．为了解学生的课外阅读情况，某校随机抽查了部分学生阅读课外书册数的情况，并绘制出如下统计图，其中条形统计图因为破损丢失了阅读 5 册书数的数据． (1) 求条形图中丢失的数据，并写出阅读书册数的众数和中位数； (2) 根据随机抽查的这个结果，请估计该校 1200 名学生中课外阅读 5 册书的学生人数； (3) 若学校又补查了部分同学的课外阅读情况，得知这部分同学中课外阅读最少的是 6 册，将补查的情况与之前的数据合并后发现中位数并没有改变，试求最多补查了多少人？