- 2021-10-27 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
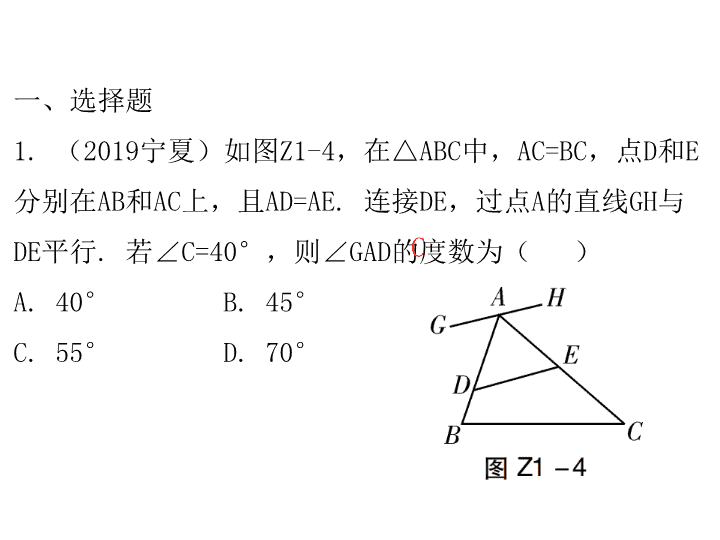
北师大版八年级下册数学专题训练课件-第1章 三角形的证明-3专题三 等腰三角形和等边三角形的性质与判定
中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中 小 学 精 品 教 学 资 源 中小学精品教学资源 中小学精品教学资源中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 中小学精品教学资源 第一章 三角形的证明 专题三 本章重要考点专练—— 等腰三角形和等边三角形的性质与判定 一、选择题 1. (2019宁夏)如图Z1-4,在△ABC中,AC=BC,点D和E 分别在AB和AC上,且AD=AE. 连接DE,过点A的直线GH与 DE平行. 若∠C=40°,则∠GAD的度数为( ) A. 40° B. 45° C. 55° D. 70° C B 2. (2019天水)如图Z1-5,等边三角形OAB的边长为2, 则点B的坐标为( ) A. (1,1) B. (1, ) C. ( ,1) D. ( , ) 二、填空题 3. (2019兰州)在△ABC中,AB=AC,∠A=40°,则 ∠B=______. 4. (2019广安)等腰三角形的两边长分别为6 cm,13 cm,其周长为______. 5. (2019成都)如图Z1-6,在△ABC中,AB=AC,点D,E 都在边BC上,∠BAD=∠CAE.若BD=9, 则CE的长为______. 70° 32 cm 9 6. (2019哈尔滨)如图Z1-7,在四边形ABCD中,AB=AD, BC=DC,∠A=60°,点E为AD边上一点,连接BD,CE,CE与 BD交于点F,且CE∥AB.若AB=8,CE=6,则BC的长为 _______. 7. 如图Z1-8,在△ABC中,BD⊥AC,∠A=50°,∠CBD =25°. 若AC=5 cm,则AB=________. 5 cm 8. 如图Z1-9,在Rt△ABC中,D,E为斜边AB上的两个点, 且BD=BC,AE=AC,则∠DCE的大小为______. 9. 如图Z1-10,△ABC是边长为6的等边三角形,DE⊥BC 于点E,EF⊥AC于点F,FD⊥AB于点D,则AD=______. 45° 2 三、解答题 10. 如图Z1-11,在△ABC中,点D在BC上. 若AB=AC=CD, BD=AD,求△ABC中各内角的度数. 解:∵AB=AC=CD, ∴∠B=∠C,∠1=∠2. ∵BD=AD, ∴∠B=∠3. 又∵∠1=∠B+∠3, ∠B+∠3+∠2+∠C=180°,即 5∠B=180°, ∴∠B=36°,∠C=36°,∠BAC=108°. 11. (2019重庆)如图Z1-12,在△ABC中,AB=AC, AD⊥BC于点D. (1)若∠C=42°,求∠BAD的度数; (2)若点E在边AB上,EF∥AC交AD的延长线于点F. 求证: AE=FE. (1)解:∵AB=AC,AD⊥BC于点D, ∴∠BAD=∠CAD,∠ADC=90°. 又∵∠C=42°, ∴∠BAD=∠CAD=90°-42°=48°. (2)证明:∵AB=AC,AD⊥BC于点D, ∴∠BAD=∠CAD. ∵EF∥AC,∴∠F=∠CAD. ∴∠BAD=∠F.∴AE=FE. 12. (2019重庆)如图Z1-13,在△ABC中,AB=AC,D是 BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过点E 作EF∥BC交AB于点F. (1)若∠C=36°,求∠BAD的度数; (2)求证:FB=FE. (1)解:∵AB=AC,∴∠ABC=∠C. ∵∠C=36°,∴∠ABC=36°. ∵BD=CD,AB=AC, ∴AD⊥BC. ∴∠ADB=90°. ∴∠BAD=90°-36°=54°. (2)证明:∵BE平分∠ABC, ∴∠ABE=∠CBE= ∠ABC. ∵EF∥BC,∴∠FEB=∠CBE. ∴∠FBE=∠FEB.∴FB=FE.查看更多