八年级上数学课件八年级上册数学课件《一定是直角三角形吗》 北师大版 (1)_北师大版

八年级上数学课件八年级上册数学课件《一定是直角三角形吗》 北师大版 (1)_北师大版

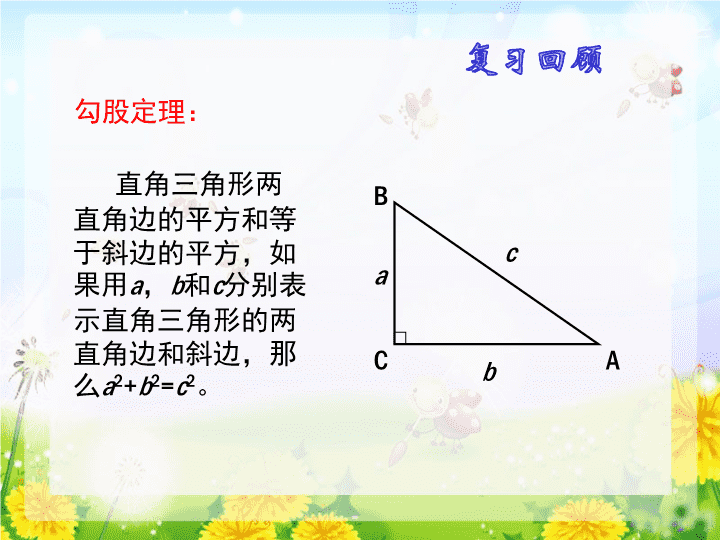
1.2 一定是直角三角形吗 学习目标 1.识记勾股定理的逆定理和勾股数 2.会判定三角形是否为直角三角形 勾股定理： 直角三角形两 直角边的平方和等 于斜边的平方，如 果用a，b和c分别 表示直角三角形的 两直角边和斜边， 那么a2+b2=c2。 A B C a b c 如果a2+b2=c2，那么这个三角形是直角三角形吗？ A B C a b c 用a，b，c分别表示三角形的三边 一．画一画 二．量一量 用量角器量一量，它们都是直角三角形吗？ 下列的三组数分别是一个三角形的 三边长a，b，c： ①3，4，5;②5，12，13;③8，15，17 分别以每组数为三边作出三角形 三．算一算 四．猜一猜 （1）三角形三边的关系？ （2）哪条边对的是直角？ a2+b2=c2 （1）两条较短的边的平方和 （2）最长边的平方 最长边对的是直角 如果三角形的三边长a，b，c满足a2+b2=c2， 那么这个三角形是直角三角形。 归纳结论 满足a2+b2=c2的三个正整数，称为勾股数。 例：3、4、5；5、12、13；8、15、17。 勾股定理的逆定理： 勾股数： 例1、一个零件的形状如图1- 16所示， 按规定这个零件中，∠A和∠DBC都应为 直角，工人师傅量得这个零件各边尺寸 如图1- 17所示，这个零件符合要求吗？ A B CD A B CD 1- 16 1- 17 3 4 13 125 例题解析 解：∵在Rt△ABD中， AB2+AD2=9+16=25=BD2 ∴△ABD是直角三角形，∠A是直角 ∵在△BCD中， BD2+BC2=25+144=169=CD2 ∴△BCD是直角三角形，∠DBC是直角 因此这个零件符合要求 1.下面以a、b、c为边长的△ABC是不是直角三角形？ 如果是，那么哪一个角是直角？ (1) a=9 b=12 c=15 ； 。 (2) a=12 b=18 c=22 ； 。 (3) a=12 b=35 c=36 ； 。 当堂练习 不是 是 不是 ∠ c=900 2、如图，在正方形ABCD中，AB=4，AE=2， DF=1，图中有几个直角三角形，你是如何判断 的？与你的同伴交流。 4 2 2 1 3 4 BE2=42+22=20 FE2=12+22=5 FB2=32+42=25 BE2+FE2=FB2 课堂小结 1. 勾股定理逆定理可以判断一个三角 形是否为直角三角形 2. 勾股数 例3/4/5；5/12/13；8/12/17 课后作业 1. 课本 P10 1.3 1、2 2. 绩优学案P8达标测评