八年级数学上册第三章中心对称图形（一）3-6三角形、梯形的中位线（第1课时）三角形的中位线课件苏教版

八年级数学上册第三章中心对称图形（一）3-6三角形、梯形的中位线（第1课时）三角形的中位线课件苏教版

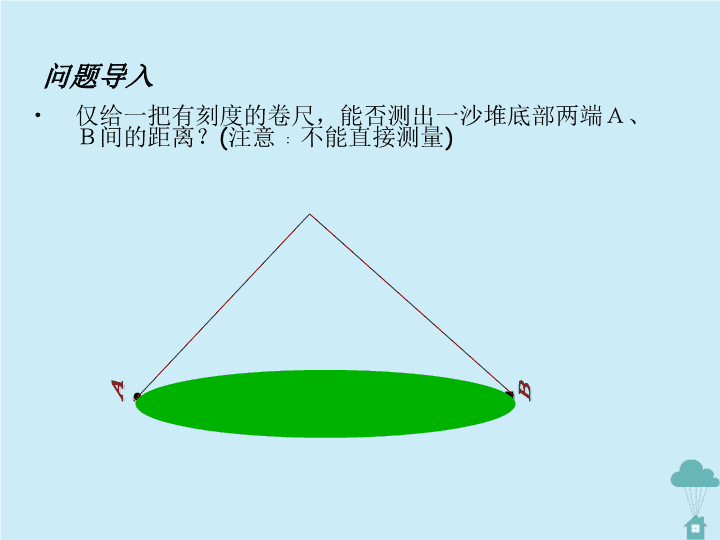
问题导入 • 仅给一把有刻度的卷尺，能否测出一沙堆底部两端Ａ、 Ｂ间的距离？(注意﹕不能直接测量) ． · 情景创设 • 怎样将一张三角形纸片剪成两部分，使分成的 两部分能拼成一个平行四边形？ • 1。剪一个三角形，记为ΔABC 2．分别取AB、AC的中点D、E，并连接DE 3．沿DE将ΔABC剪成两部分，并将ΔADE绕点E旋转180°得四边形DBCF 　 做一做： v 四边形DBCF是什么特殊的四边形？为什么？ 想一想： 答：四边形DBCF是平行四边形。 由操作可知：ΔADE与ΔCFE关于点E成中心对称 则CF=AD,∠F=∠ADE 由∠F=∠ADE可得：AB∥CF 又由CF=AD，AD=DB可得：DB=CF 所以四边形BCFD是平行四边形　理由：一组对边平行且 相等的四边形是平行四边形 A B C D E F 图中线段DE 是连接ΔABC两边的 中点D、E所得的线段，称此线段 DE为ΔABC的中位线 读一读： 三角形中位线的概念　 连接三角形两边的中点的线段叫做三角形的中位线 三角形的中位线与三角形的中线的区别是什么？　 答：三角形的中位线的两端都是中点 三角形的中线一端是中点，另一端是顶点 想一想： A B C E 议一议： ΔABC的中位线DE与BC有怎样的位置和数量关系？ 为什么？ 答：DE∥BC，DE=½BC 通过探索得知：四边形BCFD是平行四边形 则DF∥BC DF=BC 即DE∥BC DE=½DF=½BC 三角形中位线的性质: 三角形的中位线平行与第三边，并且等于它的一半。 说明　此性质的特点：同一条件下有2个结论 因为DE为ΔABC的中位线 所以①DE∥BC，②DE=½BC ↓ ↓ 位置关系 数量关系 A B C E F 试一试： 你能解决本节课开始提出的问题了吗？ 解答：先在沙堆外取一点C， 连接 CA、CB 再取 CA、CB 的中点D、E,并量得D、E间的距 离，假设其大小为 m 则A、B 间的距离为 2m 。 根据是： 三角形 的中位线等于第三边的一半 A B C D Em 2m 例题解析 • 猜一猜：画一个任意四边形，并画出四边的中点，再顺次连 接四边形的中点，得到的四边形的形状是什么？ v如图，四边形ABCD中，E F G H分别是 AB CD AD BC的中点，四边形EFGH是 平行四边形吗？为什么？ v解：四边形EFGH是平行四边形 连接DB 因为E、H分别是AB、AD的中点 ， 即EH是ΔABD的中位线 所以EH∥BD，EH=½ BD，理由是：三角形的中位线平行于第三 边，并且等于它的一半。 同理可得，FG∥BD FG=½BD 所以EH∥FG，EH=FG 故四边形EFGH是平行四边形，理由是；一组对边平行 且相等的四边形是平行四边形 A B C D H E F G ⑴顺次连接任意四边形四边中点所得的四边形是平行四边形 议一议： v顺次连接矩形的四边中点所得的四边形是什么形状？为 什么？ 如果将“矩形”改成“菱形”呢？ ⑵顺次连接矩形的四边中点所得的四边形是菱形 ⑶顺次连接菱形的四边中点所得的四边形是矩形 结论：　 (1) (2) (3) 课堂训练 • 练一练：1。如图（1）ΔABC中， AB=6㎝， AC=8㎝，BC=10㎝， D﹑E﹑F分别是ABACBC的中点 则ΔDEF的周长是＿＿＿＿ ， 面积是＿＿＿＿。 v2．如图（2）ΔABC中，DE是 中位线，AF是中线，则DE与 AF的关系是＿＿＿＿ v3．若顺次连接四边形四边中 点所得的四边形是菱形，则 原四边形（ 　） （A）一定是矩形 （B）一定是菱形 （C）对角线一定互相垂直　 （D）对角线一定相等 F A B c D E (1) A C B D E F (2) 互相平分 6cm2 12cm D 议一议： • 1.如果顺次连接四边形四边中点所得的四边形是菱形，那么 原四边形的两条对角线存在什么关系 ？ （两条对角线相等） v2.上问中的菱形改为矩形呢？ （两条对角线互相垂直） v3.当四边形满足什么条件时，顺次连接它的四边中点 所得的四边形是正方形？ （两条对角线互相垂直且相等） • ４．如图,梯形ABCD中，AD∥BC，E﹑F分别是AC﹑BD的中点 （１）EF与AD﹑BC的关系如何？为什么？　 （２）若AD=a，BC=b，求EF的长。 　　 A B C D E F G 解：（１）AD∥EF∥BC　 因为AD∥BC　，则∠DAF＝∠GCF，∠ADF＝∠CGF 连接DF并延长DF交BC于G 又AF＝FC 所以△ADF≌△CFG(AAS) 所以DF=FG 而DE=EB 所以EF∥ BC　　 理由是：三角形的中位线平行于第三边 又AD∥BC 所以AD∥EF∥BC v ４．如图,梯形ABCD中，AD∥BC，E﹑F分别是AC﹑BD的中点 （１）EF与AD﹑BC的关系如何？为什么？　 （２）若AD=a，BC=b，求EF的长。 　　 A E G D F C B 解：（2） 所以EF=BG=½(BC-GC)　 理由是：三角形的中位线 等于第三边的一半。 而GC=AD 所以EF=½(BC-AD)=½(b-a) 由（１）可知：EF是△DBG的中位线 探索研究： 　已知：△ABC的周长为a，面积为s，连接各边中点得 △A1B1C1，再连接△A1B1C1各边中点得△A2B2C2 ……， 则（１）　第３次连接所得 　　　　△A3B3C3的周长＝＿＿＿＿,面积＝＿＿＿＿　　　　 （２）第n次连接所得 　　　　△AnBnCn的周长＝＿＿＿＿，面积＝＿＿＿＿　　　　　　　　 A B C 次序 1 2 3 …… n 所得三角形 周长 …… 得三角形面 积所 …… 64 s 1 16 s 1 4 s1 n4 s 1 4 a 1 2 a 1 8 a 1 2 a 1 n 8 a1 64 s 1 2 a 1 n 4 s1 n A１ B１ C１ A２ B２ C２ v分析：填表 本课小结 • １．理解三角形中位线的概念：连接三角形 两边的中点的线段叫做三角形的中位线。 • ２．掌握三角形中位线的性质：三角形的中 位线平行与第三边，并且等于它的一半。 • 3．能应用三角形中位线的性质解决有关计算 或说理等问题。