- 2021-10-27 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师大版八年级数学上册期末测试题含答案
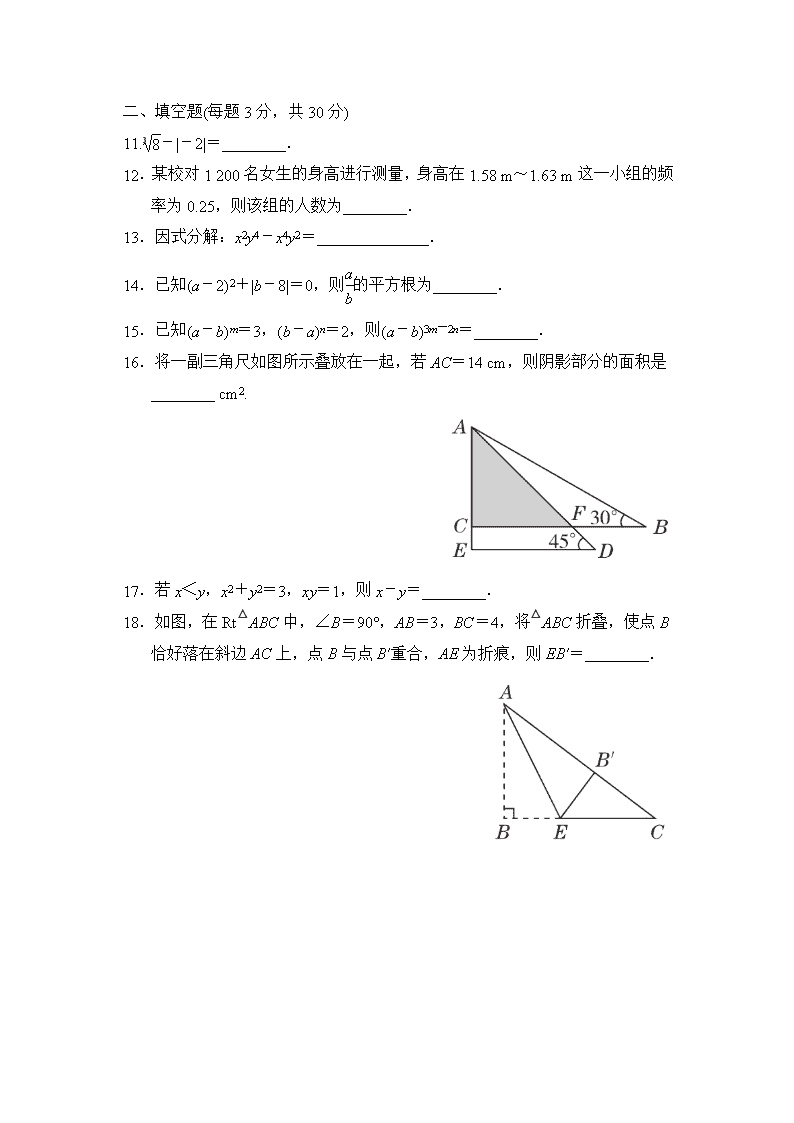
华师大版八年级数学上册期末测试题含答案 一、选择题(每题 3 分,共 30 分) 1.实数3 27,0,-π,16,1 3 ,0.101 001 000 1…(相邻两个 1 之间依次多一个 0), 其中无理数有( ) A.1 个 B.2 个 C.3 个 D.4 个 2.下面各式中,计算正确的是( ) A.2x+3y=5xy B.x6÷x2=x3 C.x2·x3=x5 D.(-x3)3=x6 3.下列长度的四组线段中,可以构成直角三角形的是( ) A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1, 2,3 4.下列因式分解中,正确的个数为( ) ①x3+2xy+x=x(x2+2y);②x2+4x+4=(x+2)2;③-x2+y2=(x+y)(x-y). A.3 个 B.2 个 C.1 个 D.0 个 5.估计 13+1 的值在( ) A.2 到 3 之间 B.3 到 4 之间 C.4 到 5 之间 D.5 到 6 之间 6.下列命题中,正确的是( ) A.如果|a|=|b|,那么 a=b B.一个角的补角一定大于这个角 C.直角三角形的两个锐角互余 D.一个角的余角一定小于这个角 7.如图,已知∠1=∠2,则不一定能使 △ ABD≌△ACD 的条件是( ) A.BD=CD B.AB=AC C.∠B=∠C D.AD 平分∠BAC 8.如图所示,所提供的信息正确的是( ) A.七年级学生最多 B.九年级的男生人数是女生人数的 2 倍 C.九年级女生比男生多 D.八年级比九年级的学生多 9.如图,在 △ MNP 中,∠P=60°,MN=NP,MQ⊥PN,垂足为 Q,延长 MN 至点 G,取 NG=NQ,若 △ MNP 的周长为 12,MQ=a,则 △ MGQ 的周长是 ( ) A.8+2a B.8+a C.6+a D.6+2a 10.如图,在 △ ABC 中,∠C=90°,∠B=30°,以 A 为圆心,任意长为半径画 弧分别交 AB,AC 于点 M 和 N,再分别以 M,N 为圆心,大于 1 2MN 的长为 半径画弧,两弧交于点 P,连结 AP,并延长交 BC 于点 D,则下列说法中正 确的个数是( ) ①AD 是∠BAC 的平分线;②∠ADC=60°;③点 D 在 AB 的垂直平分线上; ④S △ DAC:S △ DAB=CD:DB=AC:AB. A.1 B.2 C.3 D.4 二、填空题(每题 3 分,共 30 分) 11.3 8-|-2|=________. 12.某校对 1 200 名女生的身高进行测量,身高在 1.58 m~1.63 m 这一小组的频 率为 0.25,则该组的人数为________. 13.因式分解:x2y4-x4y2=______________. 14.已知(a-2)2+|b-8|=0,则a b 的平方根为________. 15.已知(a-b)m=3,(b-a)n=2,则(a-b)3m-2n=________. 16.将一副三角尺如图所示叠放在一起,若 AC=14 cm,则阴影部分的面积是 ________ cm2. 17.若 x<y,x2+y2=3,xy=1,则 x-y=________. 18.如图,在 Rt △ ABC 中,∠B=90°,AB=3,BC=4,将 △ ABC 折叠,使点 B 恰好落在斜边 AC 上,点 B 与点 B′重合,AE 为折痕,则 EB′=________. 19.四个全等的直角三角形按如图所示方式围成正方形 ABCD,过各较长直角边 的中点作垂线,围成面积为 S 的小正方形 EFGH,已知 AM 为 Rt △ ABM 较长 直角边,AM2=8EF2,则正方形 ABCD 的面积为________. 20.阅读下面材料. 在数学课上,老师提出如下问题: 小芸的作法如下: 老师说:“小芸的作法正确.” 请回答:小芸的作图依据是_________________________________________. 三、解答题(21,22 题每题 6 分,23,24 题每题 8 分,25,26 题每题 10 分,27 题 12 分,共 60 分) 21.计算或因式分解: (1) 16-|-3|+(-4)×2-1; (2)a3-a2b+1 4ab2; (3)(x+1)2+x(x-2)-(x +1)(x-1). 22.先化简,再求值:(x+y)(x-y)+(4xy3-8x2y2)÷4xy,其中 x=1,y=1 2. 23.如图,在 △ ABC 和 △ ADE 中,AB=AC,AD=AE,∠BAC=∠DAE,点 C 在 DE 上. 求证:(1) △ ABD≌△ACE; (2)∠BDA=∠ADE. 24.某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项, 现随机抽查了 m 名学生,并将其结果绘制成如图所示不完整的条形统计图 和扇形统计图. 请结合以上信息解答下列问题: (1)m=________; (2)请补全上面的条形统计图; (3)在图②中,“乒乓球”所对应扇形的圆心角的度数为________. 25.如图,在 △ ABC 中,∠C=90°,把 △ ABC 沿直线 DE 折叠,使 △ ADE 与 △ BDE 重合. (1)若∠A=35°,则∠CBD 的度数为________; (2)若 AC=8,BC=6,求 AD 的长; (3)当 AB=m(m>0), △ ABC 的面积为 m+1 时,求 △ BCD 的周长.(用含 m 的代数 式表示) 26.如图,∠ABC=90°,点 D,E 分别在 BC,AC 上,AD⊥DE,且 AD=DE, 点 F 是 AE 的中点,FD 的延长线与 AB 的延长线相交于点 M. (1)求证:∠FMC=∠FCM; (2)AD 与 MC 垂直吗?并说明理由. 27.如图,在 △ ABC 中,AB=AC=2,∠B=40°,点 D 在线段 BC 上运动(D 不 与 B,C 重合),连结 AD,作∠ADE=40°,DE 交线段 AC 于 E. (1)当∠BDA=115°时,∠BAD=________°,∠DEC=________°,点 D 从 B 向 C 运动时,∠BDA 逐渐变________(填“大”或“小”); (2)当 DC 等于多少时, △ ABD 与 △ DCE 全等?请说明理由. (3)在点 D 的运动过程中, △ ADE 的形状可以是等腰三角形吗?若可以,请 直接写出∠BDA 的度数.若不可以,请说明理由. 答案 一、1.B 2.C 3.B 4.C 5.C 6.C 7.B 8.B 9.D 10.D 点拨:④过点 D 作 AB 的垂线,再利用等高的两个三角形的面积之比等 于底之比判断. 二、11.0 12.300 13.x2y2(y+x)(y-x) 14.±1 2 15.27 4 点拨:(a-b)3m - 2n =(a-b)3m÷(a-b)2n=[(a-b)m]3÷[(a-b)n]2=[(a- b)m]3÷[(b-a)n]2=33÷22=27 4 . 16.98 17.-1 点拨:(x-y)2=x2+y2-2xy=3-2×1=1,∵x<y,∴x-y<0,∴x- y=- 1=-1. 18.3 2 点拨:在 Rt △ ABC 中,∠B=90°,AB=3,BC=4,∴AC=5. 由折叠可得,B′E=BE,AB′=AB=3,∠AB′E=∠B=90°. 设 BE=B′E=x,则 EC=4-x,B′C=5-3=2,在 Rt △ B′EC 中,由勾股定理得 EC2=B′C2+B′E2,即(4-x)2=22+x2,解得 x=3 2. 19.9S 点拨:设 AM=2a,BM=b.则正方形 ABCD 的面积=4a2+b2,由题意 可知 EF=(2a-b)-2(a-b)=2a-b-2a+2b=b.∵AM2=8EF2,∴4a2=8b2. ∵正方形 EFGH 的面积为 S, ∴b2=S,∴正方形 ABCD 的面积=4a2+b2=9b2=9S. 20.到线段两端距离相等的点在线段的垂直平分线上,两点确定一条直线 三、21.解:(1)原式=4-3-2=-1. (2)原式=a a2-ab+1 4b2 =a a-1 2b 2 . (3)原式=(x+1)(x+1-x+1)+x(x-2)=2(x+1)+x(x-2)=x2-2x+2x+2=x2 +2. 22.解:原式=x2-y2+y2-2xy=x2-2xy,当 x=1,y=1 2 时,原式=1-2×1×1 2 = 0. 23.证明:(1)∵∠BAC=∠DAE, ∴∠BAC-∠DAC=∠DAE-∠DAC, ∴∠BAD=∠CAE. 又 AB=AC,AD=AE, ∴△ABD≌△ACE(S.A.S.). (2)由 △ ABD≌△ACE,可得∠BDA=∠E.又 AD=AE, ∴∠ADE=∠E,∴∠BDA=∠ADE. 24.解:(1)150 (2)补全条形统计图如图. (3)36° 25.解:(1) 20° (2)由题易知 AD=BD.设 AD=x, 则 BD=x,DC=8-x. 在 Rt △ BCD 中,DC2+BC2=BD2, 即(8-x)2+62=x2, 解得 x=25 4 .∴AD 的长为25 4 . (3)由题意知:AC2+BC2=m2, 1 2AC·BC=m+1, ∴(AC+BC)2-2AC·BC=m2, ∴(AC+BC)2=m2+2AC·BC= m2+4(m+1)=(m+2)2, ∴AC+BC=m+2, ∴△BCD 的周长=DB+DC+BC=AD+DC+BC=AC+BC=m+2. 26.(1)证明:∵△ADE 是等腰直角三角形,点 F 是 AE 的中点, ∴DF⊥AE,∠ADF=∠EDF=45°, ∠DAF=∠AED=45°, ∴DF=AF=EF. ∵∠ABC=90°,∴∠BAC+∠DCF=90°. ∵MF⊥AE,∴∠AMF+∠BAC=90°. ∴∠DCF=∠AMF. 在 △ DFC 和 △ AFM 中, ∠DCF=∠AMF, ∠CFD=∠MFA=90°, DF=AF, ∴△DFC≌△AFM(A.A.S.), ∴CF=MF,∴∠FMC=∠FCM. (2)解:AD⊥MC.理由如下:由(1)知,∠MFC=90°,FD=EF,FM=FC, ∴∠FDE=∠FMC=45°,∴DE∥CM. 又∵AD⊥DE,∴AD⊥MC. 27.解:(1)25;115;小 (2)当 DC=2 时, △ ABD≌△DCE.理由如下:∵AB=AC,∴∠C=∠B=40°, ∴∠DEC+∠EDC=140°. 又∵∠ADE=40°, ∴∠ADB+∠EDC=140°, ∴∠ADB=∠DEC. 又∵AB=DC=2, ∴△ABD≌△DCE(A.A.S.). (3)可以.∠BDA 的度数为 110°或 80°.查看更多