八上时 公式法二

八上时 公式法二

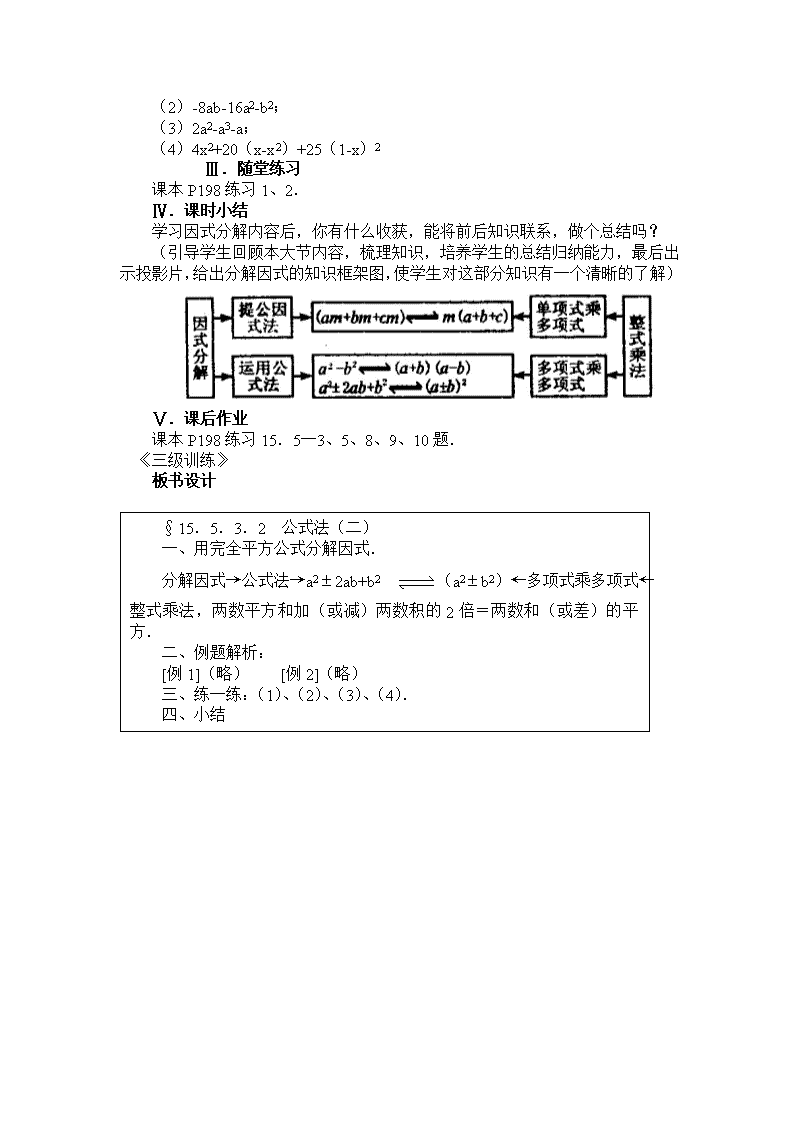
‎§15．5．3．2 公式法（二）‎ ‎ 教学目标 ‎ （一）教学知识点 ‎ 用完全平方公式分解因式 ‎ （二）能力训练要求 ‎ 1．理解完全平方公式的特点．‎ ‎ 2．能较熟悉地运用完全平方公式分解因式．‎ ‎ 3．会用提公因式、完全平方公式分解因式，并能说出提公因式在这类因式分解中的作用．‎ ‎ 4．能灵活应用提公因式法、公式法分解因式．‎ ‎ （三）情感与价值观要求 ‎ 通过综合运用提公因式法，完全平方公式分解因式，进一步培养学生的观察和联想能力．通过知识结构图培养学生归纳总结的能力．‎ ‎ 教学重点 ‎ 用完全平方公式分解因式．‎ ‎ 教学难点 ‎ 灵活应用公式分解因式．‎ ‎ 教学方法 ‎ 探究与讲练相结合的方法．‎ ‎ 教具准备 ‎ 投影片．‎ ‎ 教学过程 ‎ Ⅰ．提出问题，创设情境 ‎ 问题1：根据学习用平方差公式分解因式的经验和方法，分析和推测什么叫做运用完全平方公式分解因式？能够用完全平方公式分解因式的多项式具有什么特点？‎ ‎ 问题2：把下列各式分解因式．‎ ‎ （1）a2+2ab+b2‎ ‎ （2）a2-2ab+b2‎ ‎ [生]将整式乘法的平方差公式反过来写即是分解因式的平方差公式．同样道理，把整式乘法的完全平方公式反过来写即分解因式的完全平方公式．‎ ‎ [师]能不能用语言叙述呢？‎ ‎ [生]能．两个数的平方和，加上（或减去）这两数的积的2倍，等于这两个数的和（或差）的平方．‎ ‎ 问题2其实就是完全平方公式的符号表示．即：a2+2ab+b2=（a+b）2，a2-2ab+b2（a-b）2．‎ ‎ [师]今天我们就来研究用完全平方公式分解因式．‎ ‎ Ⅱ．导入新课 ‎ 出示投影片 ‎ 下列各式是不是完全平方式？‎ ‎ （1）a2‎-4a+4‎ ‎ （2）x2+4x+4y2‎ ‎ （3）‎4a2+2ab+b2‎ ‎ （4）a2-ab+b2‎ ‎ （5）x2-6x-9‎ ‎ （6）a2+a+0.25‎ ‎ （放手让学生讨论，达到熟悉公式结构特征的目的）．‎ ‎ 结果：（1）a2‎-4a+4=a2-2×2·a+22=（a-2）2‎ ‎ （3）‎4a2+2ab+b2=（‎2a）2+2×‎2a·b+（b）2=（‎2a+b）2‎ ‎ （6）a2+a+0.25=a2+2·a·0.5+0.52=（a+0.5）2‎ ‎ （2）、（4）、（5）都不是．‎ ‎ 方法总结：分解因式的完全平方公式，左边是一个二次三项式，其中有两个数的平方和还有这两个数的积的2倍或这两个数的积的2倍的相反数，符合这些特征，就可以化成右边的两数和（或差）的平方．从而达到因式分解的目的．‎ ‎ 例题解析 ‎ 出示投影片 ‎ [例1]分解因式：‎ ‎ （1）16x2+24x+9 （2）-x2+4xy-4y2‎ ‎ [例2]分解因式：‎ ‎ （1）3ax2+6axy+3ay2 （2）（a+b）2-12（a+b）+36‎ ‎ 学生有前一节学习公式法的经验，可以让学生尝试独立完成，然后与同伴交流、总结解题经验．‎ ‎ [例1]（1）分析：在（1）中，16x2=（4x）2，9=32，24x=2·4x·3，所以16x2+14x+9是一个完全平方式，即 ‎ 解：（1）16x2+24x+9‎ ‎ =（4x）2+2·4x·3+32‎ ‎ =（4x+3）2．‎ ‎ （2）分析：在（2）中两个平方项前有负号，所以应考虑添括号法则将负号提出，然后再考虑完全平方公式，因为4y2=（2y）2，4xy=2·x·2y．‎ ‎ 所以：‎ ‎ 解：-x2+4xy-4y2=-（x2-4xy+4y2）‎ ‎ =-[x2-2·x·2y+（2y）]2‎ ‎ =-（x-2y）2．‎ ‎ 练一练：‎ ‎ 出示投影片 ‎ 把下列多项式分解因式：‎ ‎ （1）‎6a-a2-9；‎ ‎ （2）-8ab‎-16a2-b2；‎ ‎ （3）‎2a2-a3-a；‎ ‎ （4）4x2+20（x-x2）+25（1-x）2‎ ‎ Ⅲ．随堂练习 ‎ 课本P198练习1、2．‎ ‎ Ⅳ．课时小结 ‎ 学习因式分解内容后，你有什么收获，能将前后知识联系，做个总结吗？‎ ‎ （引导学生回顾本大节内容，梳理知识，培养学生的总结归纳能力，最后出示投影片，给出分解因式的知识框架图，使学生对这部分知识有一个清晰的了解）‎ ‎ Ⅴ．课后作业 ‎ 课本P198练习15．5─3、5、8、9、10题．‎ ‎《三级训练》‎ ‎ 板书设计 ‎ ‎ ‎ §15．5．3．2 公式法（二）‎ ‎ 一、用完全平方公式分解因式．‎ ‎ 分解因式→公式法→a2±2ab+b2 （a2±b2）←多项式乘多项式←整式乘法，两数平方和加（或减）两数积的2倍＝两数和（或差）的平方．‎ ‎ 二、例题解析：‎ ‎ [例1]（略） [例2]（略）‎ ‎ 三、练一练：（1）、（2）、（3）、（4）．‎ ‎ 四、小结 ‎ ‎