八年级数学上册第一章勾股定理1-1探索勾股定理同步练习 北师大版

八年级数学上册第一章勾股定理1-1探索勾股定理同步练习 北师大版

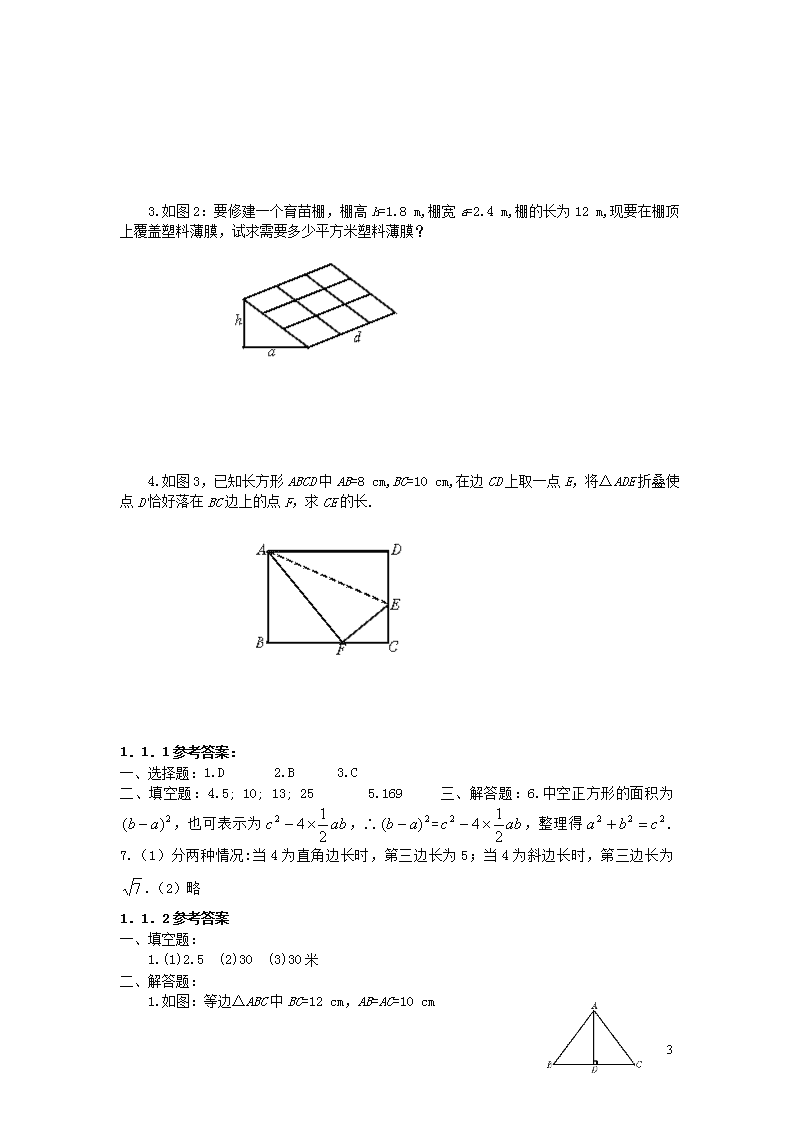
1 c a b a c b b c b a a c 1 探索勾股定理 在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗？ 它的意思是说：如果一个直角三角形的两条直角边长分别为 3 和 4 个长度单位，那么它 的斜边的长一定是 5 个长度单位，而且 3、4、5 这三个数有这样的关系：32+42=52. （1）请你动动脑筋，能否验证这个事实呢？该如何考虑呢？ （2）请你观察下列图形，直角三角形 ABC 的两条直角边的长分别为 AC=7，BC=4，请你 研究这个直角三角形的斜边 AB 的长的平方是否等于 42+72？ 一、选择题： 1. 下列说法正确的是（ ） A.若 a、b、c 是△ABC 的三边，则 a2＋b2＝c2 B.若a、b、c是Rt△ABC的三边，则a2＋b2＝c2 C.若 a、b、c 是 Rt△ABC 的三边， 90A ，则 a2＋b2＝c2 D.若 a、b、c 是 Rt△ABC 的三边， 90C ，则 a2＋b2＝c2 2. △ABC 的三条边长分别是 a 、b 、 c ，则下列各式成立的是（ ） A． cba  B. cba  C. cba  D. 222 cba  3．一个直角三角形中，两直角边长分别为 3 和 4，下列说法正确的是（ ） A．斜边长为 25 B．三角形周长为 25 C．斜边长为 5 D．三角形面积为 20 二、填空题： 4．在 中， 90C ， （1）如果 a=3，b=4，则 c= ； （2）如果 a=6，b=8，则 c= ； （3）如果 a=5，b=12，则 c= ； (4) 如果 a=15，b=20，则 c= . 5．如图,三个正方形中的两个的面积 S1＝25，S2＝144，则另一个的 面积 S3 为________． 三、解答题： 6．利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．观察图形， 验证：c2＝a2＋b2 . 2 7．下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题: 学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题: “已知直角三角形 ABC 的两边长分别为 3 和 4, 请你求出第三边.” 同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是 5”; 王华同学说: “第三 边长是 7 .” 还有一些同学也提出了不同的看法…… （1）假如你也在课堂上, 你的意见如何? 为什么? （2）通过上面数学问题的讨论, 你有什么感受? (用一句话表示) 1.1.2 探索勾股定理 一.填空题 (1)某养殖厂有一个长 2 米、宽 1.5 米的矩形栅栏，现在要在相对角的顶点间加固一条 木板，则木板的长应取米. (2)有两艘渔船同时离开某港口去捕鱼，其中一艘以 16 海里/时的速度向东南方向航行， 另一艘以 12 海里/时的速度向东北方向航行，它们离开港口一个半小时后相距海里. (3)如图 1：隔湖有两点 A、B，为了测得 A、B 两点间的距离，从与 AB 方向成直角的 BC 方向上任取一点 C，若测得 CA=50 m,CB=40 m，那么 A、B 两点间的距离是_________. 图 1 二、解答题： 1.已知一个等腰三角形的底边和腰的长分别为 12 cm 和 10 cm，求这个三角形的面积. 2.在△ABC 中，∠C=90°,AC=2.1 cm,BC=2.8 cm （1）求这个三角形的斜边 AB 的长和斜边上的高 CD 的长. （2）求斜边被分成的两部分 AD 和 BD 的长. 3 3.如图 2：要修建一个育苗棚，棚高 h=1.8 m,棚宽 a=2.4 m,棚的长为 12 m,现要在棚顶 上覆盖塑料薄膜，试求需要多少平方米塑料薄膜？ 4.如图 3，已知长方形 ABCD 中 AB=8 cm,BC=10 cm,在边 CD 上取一点 E，将△ADE 折叠使 点 D 恰好落在 BC 边上的点 F，求 CE 的长. 1．1．1 参考答案： 一、选择题：1.D 2.B 3.C 二、填空题：4.5; 10; 13; 25 5.169 三、解答题：6.中空正方形的面积为 2)( ab  ，也可表示为 abc 2 142  ，∴ 2)( ab  = abc 2 142  ，整理得 222 cba  . 7.（1）分两种情况:当 4 为直角边长时，第三边长为 5；当 4 为斜边长时，第三边长为 7 . （2）略 1．1．2 参考答案 一、填空题： 1.(1)2.5 (2)30 (3)30 米 二、解答题： 1.如图：等边△ABC 中 BC=12 cm，AB=AC=10 cm 4 作 AD⊥BC，垂足为 D，则 D 为 BC 中点，BD=CD=6 cm 在 Rt△ABD 中，AD2=AB2－BD2=102－62=64 ∴AD=8 cm ∴S△ABD= 2 1 BC·AD= 2 1 ×12×8=48(cm2) 2.解：(1)∵△ABC 中，∠C=90°，AC=2.1 cm，BC=2.8 cm ∴AB2=AC2+BC2=2.12+2.82=12.25 ∴AB=3.5 cm ∵S△ABC= 2 1 AC·BC= 2 1 AB·CD ∴AC·BC=AB·CD ∴CD= AB BCAC  = 5.3 8.21.2  =1.68(cm) (2)在 Rt△ACD 中，由勾股定理得： AD2+CD2=AC2 ∴AD2=AC2－CD2=2.12－1.682 =(2.1+1.68)(2.1－1.68) =3.78×0.42=2×1.89×2×0.21 =22×9×0.21×0.21 ∴AD=2×3×0.21=1.26(cm) ∴BD=AB－AD=3.5－1.26=2.24(cm) 3.解：在直角三角形中，由勾股定理可得：直角三角形的斜边长为 3 m,所以矩形塑料 薄膜的面积是：3×12=36(m2) 4.解：根据题意得：Rt△ADE≌Rt△AEF ∴∠AFE=90°,AF=10 cm,EF=DE 设 CE=x cm，则 DE=EF=CD－CE=8－x 在 Rt△ABF 中由勾股定理得： AB2+BF2=AF2，即 82+BF2=102， ∴BF=6 cm ∴CF=BC－BF=10－6=4(cm) 在 Rt△ECF 中由勾股定理可得： EF2=CE2+CF2，即(8－x)2=x2+42 ∴64－16x+x2=x2+16 ∴x=3(cm),即 CE=3 cm