- 2021-10-26 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学8年级教案:第19讲 期末备考(一)
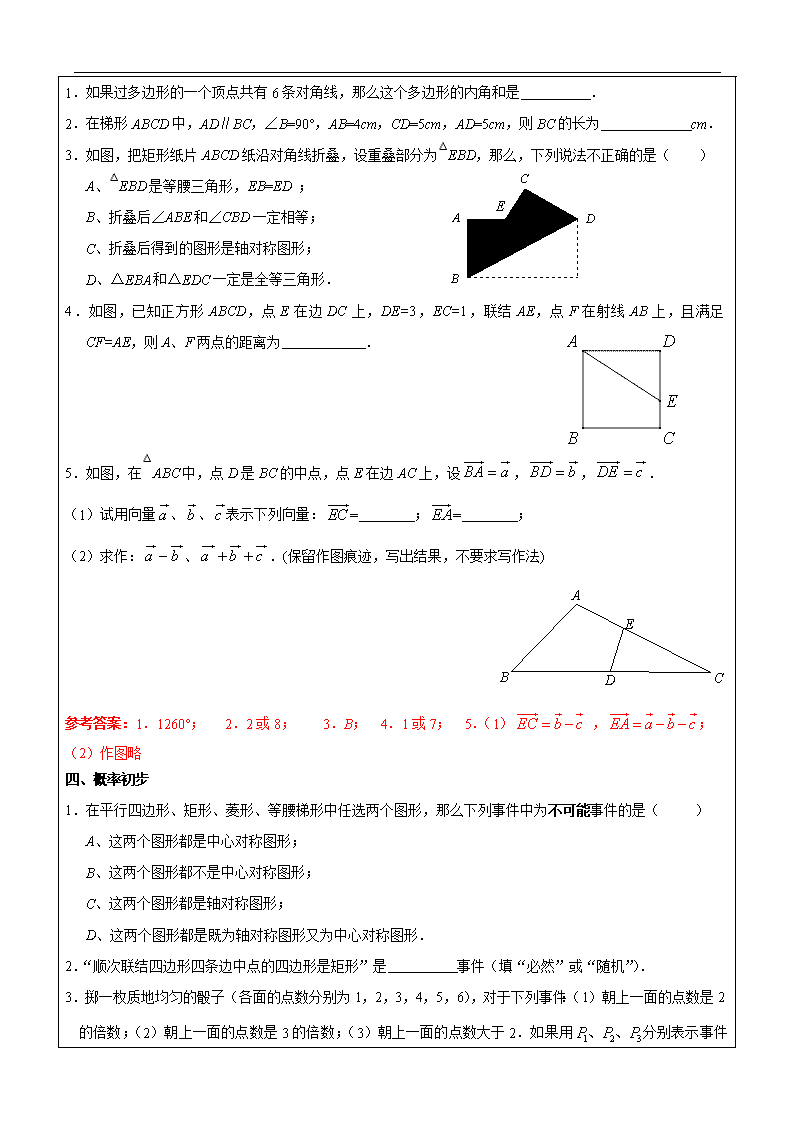
辅导教案 学员姓名: 学科教师: 年 级: 辅导科目: 授课日期 ××年××月××日 时 间 A / B / C / D / E / F段 主 题 期末备考(一) 教学内容 1.综合复习八年级下所有知识点并模拟测试. (此环节设计时间在10-15分钟) 教法说明:首先对上次课的预习思考中的期末小测试卷进行讲评。再通过思维导图对八年级第二学期内容进行回顾,明确期末考试的范围和内容。 (此环节设计时间在20-30分钟) 一、一次函数 1.已知直线平行于直线,且在y轴上的截距为3,那么这条直线的解析式是 . 2.如果一次函数的图像不经过第三象限,那么实数m的取值范围是 . 3.在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图像(全程)如图所示.有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人都跑了10千米;③甲比乙先到达终点;④两人都跑了20千米.其中正确的说法是 . 参考答案:1.; 2.; 3.①②④; 二、代数方程 1.对于二项方程,当n为偶数时,已知方程有两个实数根,那么下列不等式成立的是( ) A、; B、; C、; D、. 2.方程的根是 . 3.二元二次方程可以化成两个一次方程,那么这两个一次方程分别是 . 4.关于x的方程:的解是 ; 5.设,则分式方程化为关于y的一元二次方程的是 . 参考答案:1.A; 2.; 3.; 4.; 5.. 三、四边形 1.如果过多边形的一个顶点共有6条对角线,那么这个多边形的内角和是 . 2.在梯形ABCD中,AD∥BC,∠B=90°,AB=4cm,CD=5cm,AD=5cm,则BC的长为 cm. 3.如图,把矩形纸片ABCD纸沿对角线折叠,设重叠部分为△EBD,那么,下列说法不正确的是( ) A、△EBD是等腰三角形,EB=ED ; B、折叠后∠ABE和∠CBD一定相等; C、折叠后得到的图形是轴对称图形; D、△EBA和△EDC一定是全等三角形. 4.如图,已知正方形ABCD,点E在边DC上,DE=3,EC=1,联结AE,点F在射线AB上,且满足CF=AE,则A、F两点的距离为 . 5.如图,在△ABC中,点D是BC的中点,点E在边AC上,设,,. (1)试用向量、、表示下列向量:= ;= ; (2)求作:、.(保留作图痕迹,写出结果,不要求写作法) D E B C A 参考答案:1.1260°; 2.2或8; 3.B; 4.1或7; 5.(1) ,; (2)作图略 四、概率初步 1.在平行四边形、矩形、菱形、等腰梯形中任选两个图形,那么下列事件中为不可能事件的是( ) A、这两个图形都是中心对称图形; B、这两个图形都不是中心对称图形; C、这两个图形都是轴对称图形; D、这两个图形都是既为轴对称图形又为中心对称图形. 2.“顺次联结四边形四条边中点的四边形是矩形”是 事件(填“必然”或“随机”). 3.掷一枚质地均匀的骰子(各面的点数分别为1,2,3,4,5,6),对于下列事件:(1)朝上一面的点数是2的倍数;(2)朝上一面的点数是3的倍数;(3)朝上一面的点数大于2.如果用 分别表示事件(1)(2)(3)发生的可能性大小,那么把它们从大到小排列的顺序是 . 4.从—1,1中任取一个数作为一次函数的系数k,从—2,2中任取一个数作为一次函数 的截距b,则所得一次函数经过第一象限的概率是 . 参考答案:1.B; 2.随机; 3. 4.. 此环节设计时间在80分钟左右(60分钟练习+20分钟互动讲解)。 期末模拟测试(一) 一、填空题(本大题共10题,每题4分,共40分) 1.计算:_____________; 2.函数的图像不经过第 象限; 3.方程的根是______________; 4.一次函数的图像向下平移5个单位后,所得图像的函数解析式是 ; 5.方程有增根,则a= ; 6.已知某汽车油箱中的剩余油量y(升)与汽车行驶里程数x(千米)是一次函数关系.油箱中原有油100升,行驶60千米后的剩余油量为70升,那么行驶x (千米)后油箱中的剩余油量y=____________(升); 7.方程组的解为 ; 8.已知菱形的周长为20cm,一条对角线条为5cm,那么这个菱形的一个较大的内角为_____; 9.在1、2、3、4、5、6这个六个数字中,任意取一个数是素数的概率是 ; 10.一个等腰梯形的三条边的长分别为3cm、4cm、11cm,则其中位线长为 cm; 二、选择题(本大题共4题,每题5分,共20分) 11.下列说法正确的是( ) A、“任意两个负数的乘积为正数”,这是随机事件; B、“电视打开时正在播放广告”,这是不可能事件; C、“某人手中的玻璃杯不小心掉在水泥地面上会破碎”,这是必然事件; D、“在去掉大小王的52张扑克牌中抽13张牌,其中有1张红桃”,这是随机事件。 12.已知与是互为相反向量,那么下列关于、的式子:①;②;③;③。 上述式子正确的个数是( ) A、1 B、2 C、3 D、4 13.下列命题中,是真命题的是 ( ) A、对角线相等的四边形是矩形; B、对角线互相垂直的四边形是菱形; C、对角线互相平分的四边形是平行四边形; D、对角线互相垂直平分的四边形是正方形. 14.顺次联结平行四边形各边中点所得到的四边形一定是 ( ) A、 平行四边形; B、菱形; C、矩形; D、正方形. 三、解答题(本大题共4题,第15题10分,第16题8分,第17题10分,第18题12分,共40分) 15.(满分10分)解下列方程(组) (1)解方程:; (2)解方程组: 16.(满分8分)甲、乙两家便利店到批发站采购一批饮料,共25箱,由于两店所处的地理位置不同,因此甲 店的销售价格比乙店的销售价格每箱多10元。当两店将所进的饮料全部售完后,甲店的营业额为1000元,比 乙店少350元,求甲乙两店各进货多少箱饮料? 17.(满分10分)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,点O是BC的中点,过点O的直线l从与BC重合的位置开始绕点O作顺时针旋转,交边AB于点D,过点C作CE//AB交直线l于点E,设直线l的旋转角为α。 (1)①当α=_____度时,四边形EDAC是等腰梯形,此时BD的长为______ ______。 ②当α=_____度时,四边形EDAC是直角梯形,此时BD的长为____________。 (2)当α=90°时,猜测四边形EDAC是什么图形,请说明理由。 18.(第1问3分,第2问4分,第3问5分,满分12分) 已知:如图,在正方形ABCD中,AB=4,E为边BC延长线上的一点,联结DE,BF⊥DE,垂足为点F,BF与边CD相交于点G,联结EG;设CE=x, (1)求∠CEG的度数; (2)当BG=时,求△AEG的面积; (3)如果AM⊥BF,AM与BC相交于点M,四边形AMCD的面积为y,求y关于x的函数解析式,并写出它的定义域. 参考答案: 1.; 2.一; 3.; 4.y=2x-2; 5.3; 6.100-0.5x; 7.,,,; 8.120°; 9.; 10.; 11.D; 12.C; 13.C; 14.A; 15.(1)解:移项,得 方程两边同时平方,得. 整理,得. 解得 . 经检验是原方程的根,是增根,舍去. ∴ 原方程的根是 (2)由①得, ∴ 分别解这两个方程组,得原方程组的解是 16.解:设甲店进货x箱,乙店进货(25-x)箱, 由题意可得 ; 解得 经检验是原分式方程的解,不符合题意,舍去 15(箱) 答:甲店进货10箱,乙店进货15箱. 17.(1)①30°,2; ②60°,3 (2)当∠α=90°时,四边形EDAC是菱形. ∵∠α=∠ACB=90°, ∴AC∥ED, ∵CE∥AB, ∴四边形EDAC是平行四边形. 在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,∴∠B=30°, ∴AB=8,BC=,∴BO=. 在Rt△BOD中,∠B=30°,∴OD=2,BD=4,∴AD=4, ∴AD=AC.∴四边形EDAC是菱形. 18.(1)在正方形ABCD中,BC = CD,∠BCD =∠DCE = 90°. ∵ BF⊥DE,∴ ∠GFD = 90°. 即得 ∠BGC =∠DEC,∠GAC =∠EDC. 在△BCG和△DCE中, ∴ △BCG≌△DCE(A.S.A). ∴ GC = EC. 即得 ∠CEG = 45°. (2)在Rt△BCG中,BC = 4,, 利用勾股定理,得 CG = 2. ∴ CE = 2,DG = 2,即得 BE = 6. ∴ = 2. (3)由 AM⊥BF,BF⊥DE,易得 AM // DE. 于是,由 AD // BC,可知四边形AMED是平行四边形. ∴ AD = ME = 4. 由 CE = x,得 MC = 4 -x. ∴ . 即 . 定义域为 . (此环节设计时间在5-10分钟内) 让学生回顾本节课所学的重点知识,以学生自我总结为主,学科教师引导为辅,为本次课做一个总结回顾 【巩固练习】 期末小测试 (测试时间30分钟,满分50分) 一、选择题(本大题共3题,每题4分,满分12分) 1.下列方程没有实数根的个数是( ) A.1个; B.2个; C.3个; D.4个. 2.在四边形ABCD中,AC与BD相交于点O,要使四边形ABCD是平行四边形应符合下列条件中的( ) (A)AB∥CD,BC = AD; (B)AB = CD,OA = OC; (C)AB∥CD,OA = OC; (D)AB = CD,AC = BD. A B C D O 3.如图,在四边形ABCD中,AC与BD相交于点O,∠BAD=90º,BO=DO,那么下列条件中不能判定四边形ABCD是矩形的是( ) (A)∠ABC=90º; (B)∠BCD=90º ; (C)AB=CD; (D)AB∥CD. 二、填空题(本大题共3题,每题4分,满分12分) 4.如果方程有增根,则的值为 . 5.在梯形ABCD中,AD//BC,AD=3,BC=7,点E、F分别是AC、BD的中点,那么EF的长为 . 6.如图,在周长为20cm的□ABCD中,AB≠AD,AC、BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为 . 7.(本题12分)如图,已知梯形中,, 、分别是、的中点,点在边上,且. (1)求证:四边形是平行四边形; (2)联结,若平分,求证:四边形是矩形. 8.(本题14分)如图,在正方形ABCD中,AB=1,E为边AB上一点(点E不与端点A、B重合),F为BC延长线上一点,且AE=CF,联结EF交对角线AC于点G. (1)设,,求关于的函数解析式及定义域; (2)联结DG,求证:DG⊥EF. 答案及评分标准 一、选择题 1、 C; 2、C; 3、C。 二、填空题 4、; 5、2; 6、10。 三、解答题 7、(1)证明:联结EG, ∵ 梯形ABCD中,,且E、G分别是AB、CD的中点, ∴ EG//BC,且, 又∵ ∴ EG=BF. ∴ 四边形AEFG是平行四边形. (2)证明:设AF与EG交于点O, ∵ EG//AD,∴∠DAG=∠AGE ∵AG平分,∴∠DAG=∠GAO ∴∠GAO=∠AGE ∴ AO=GO. ∵四边形AEFG是平行四边形, ∴ AF=EG,四边形AEFG是矩形 8、(1)作EH∥CF,则△AEH为等腰直角三角形,∴,易证△EHG≌△FCG, ∴,∴, ∴ (2)联结DE,DF,易证△ADE≌△CDF,∴DE=DF,由(1)得EG=FG,∴DG⊥EF查看更多