- 2021-10-26 发布 |
- 37.5 KB |
- 7页

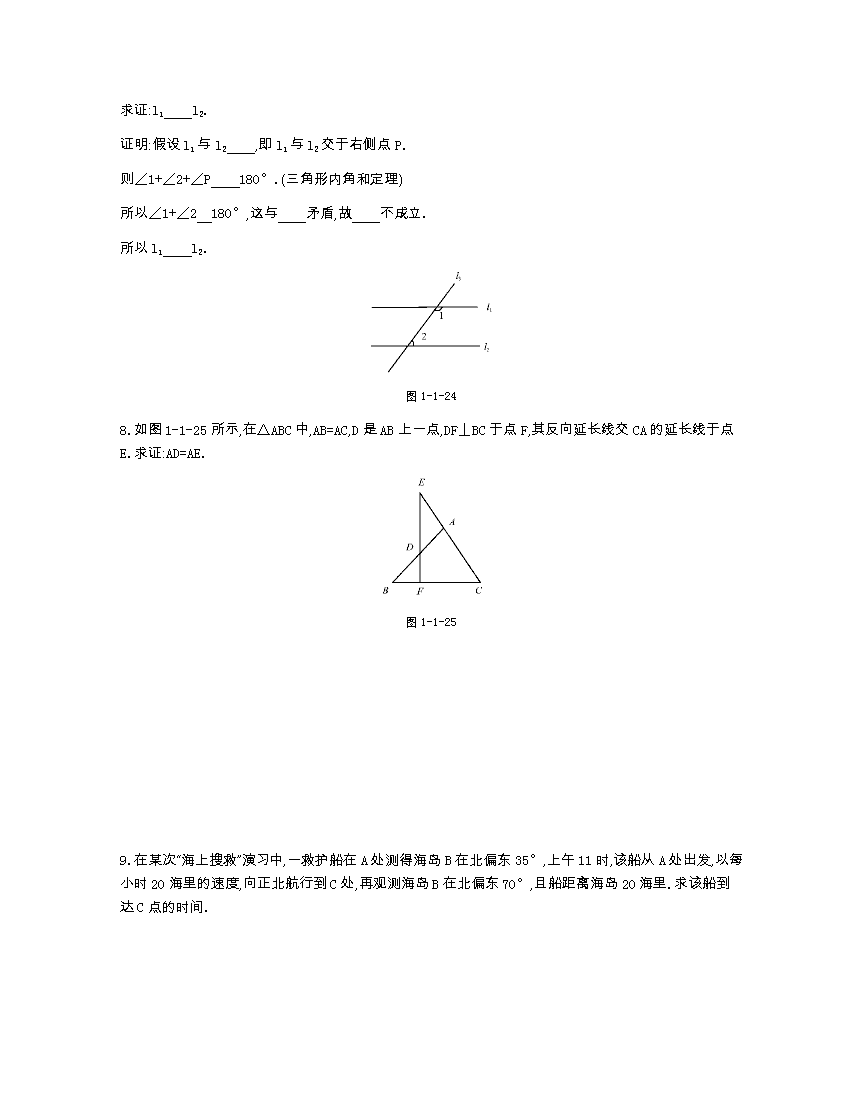

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
《同步课时卷》北师版八年级数学(下册)1
《同步课时卷》北师版八年级数学(下册) 1.1等腰三角形(第三课时) 1.等腰三角形的两底角 .简述为: . 2.有两个角 的三角形是等腰三角形.简述为: . 3.反证法是指在证明问题时,先假设 不成立,然后推导出 与 、 、 或已知条件相矛盾的结果,从而证明命题的结论一定成立. 4.要使得△ABC是等腰三角形,则需要满足下列条件中的( ) A.∠A=50°,∠B=60° B.∠A=40°,∠B=100° C.∠A+∠B=90° D.∠A-∠B=90° 5.用反证法证明命题“在直角三角形中,至少有一个锐角不大于45°”时,应先假设( ) A.有一个锐角小于45° B.每一个锐角都小于45° C.有一个锐角大于45° D.每一个锐角都大于45° 6.如图1-1-23所示,在△ABC中,DE∥BC,BE平分∠ABC,则△DBE是 三角形. 图1-1-23 7.用反证法证明(填空): 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行. 已知:如图1-1-24所示,直线l1,l2被l3所截,∠1+∠2=180°. 求证:l1 l2. 证明:假设l1与l2 ,即l1与l2交于右侧点P. 则∠1+∠2+∠P 180°.(三角形内角和定理) 所以∠1+∠2 180°,这与 矛盾,故 不成立. 所以l1 l2. 图1-1-24 8.如图1-1-25所示,在△ABC中,AB=AC,D是AB上一点,DF⊥BC于点F,其反向延长线交CA的延长线于点E.求证:AD=AE. 图1-1-25 9.在某次“海上搜救”演习中,一救护船在A处测得海岛B在北偏东35°,上午11时,该船从A处出发,以每小时20海里的速度,向正北航行到C处,再观测海岛B在北偏东70°,且船距离海岛20海里.求该船到达C点的时间. 图1-1-26 10.下面命题不正确的是( ) A.两个内角分别是50°和65°的三角形是等腰三角形 B.两个外角相等的三角形是等腰三角形 C.一个外角的平分线平行于一边的三角形是等腰三角形 D.两个内角不相等的三角形不是等腰三角形 11.用反证法证明“a≥b”时应假设( ) A.ab C.a=b D.a≤b 12.如图1-1-27所示,在△ABC中,AB=AC,BO,CO分别为∠ABC和∠ACB的平分线且相交于点O,过点O作DE∥BC交AB,AC于点D,E,图中的等腰三角形有( ) 图1-1-27 A.2个 B.3个 C.4个 D.5个 13.求证:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等. 14.如图1-1-28所示,AC=AD,∠C=∠D,求证:BC=BD. 图1-1-28 15.如图1-1-29所示,在△ABC中,AB=AC,点D在AB上,点E在BC上,DE∥AC.求证:DB=DE. 图1-1-29 16.如图1-1-30所示,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.求证:BD=DE. 图1-1-30 参考答案 1.相等等边对等角 2.相等等校对等边 3.命题的结论定义、基本事实、已有定理 4.B 5.D 6.等腰 7.∥不平行 =已知假设∥ 8.证明:∵在△ABC中,AB=AC, ∴∠B=∠C. ∵DF⊥BC, ∴∠E+∠C=90°,∠B+∠BDF=90°, ∴∠E=∠BDF. ∵∠BDF=∠ADE, ∴∠ADE=∠E, ∴AD=AE. 9.解:在△ABC中,∠MCB是△ABC的外角, ∴∠MCB=∠CAB+∠B. 又∵∠MCB=70°,∠CAB=35°, ∴∠B=∠CAB=35°. ∴AC=BC. ∴航行时间为20÷20=1(小时), ∴到达C点的时间为中午12时. 10.D 11.A 12.D 13.解:已知△ABC中,∠B≠∠C.求证:AC≠AB. 证明:假设AC=AB,则∠B=∠C,与已知矛盾,因此假设不成立,故AC≠AB. 14.证明:连接CD. ∵AC=AD, ∴∠ACD=∠ADC. 又∵∠BCD=∠ACD-∠ACB,∠BDC= ∠ADC-∠ADB,∠ACB=∠ADB, ∴∠BCD=∠BDC. ∴BC=BD. 15.证明:∵AB=AC,DE∥AC, ∴∠B=∠C,∠C=∠DEB, ∴∠B=∠DEB, ∴DB=DE. 16.证明:∵△ABC为等边三角形,BD是AC边的中线, ∴BD⊥AC,BD平分∠ABC, ∴∠DBE=∠ABC=30°. ∵CD=CE, ∴∠CDE=∠E. ∵∠ACB=60°,且∠ACB为△CDE的外角, ∴∠CDE+∠E=60°. ∴∠CDE=∠E=30°, ∴∠DBE=∠E=30°, ∴BD=DE.查看更多