八年级下册数学教案 第二章 一元一次不等式与一元一次不等式组 周周测8（2

八年级下册数学教案 第二章 一元一次不等式与一元一次不等式组 周周测8（2

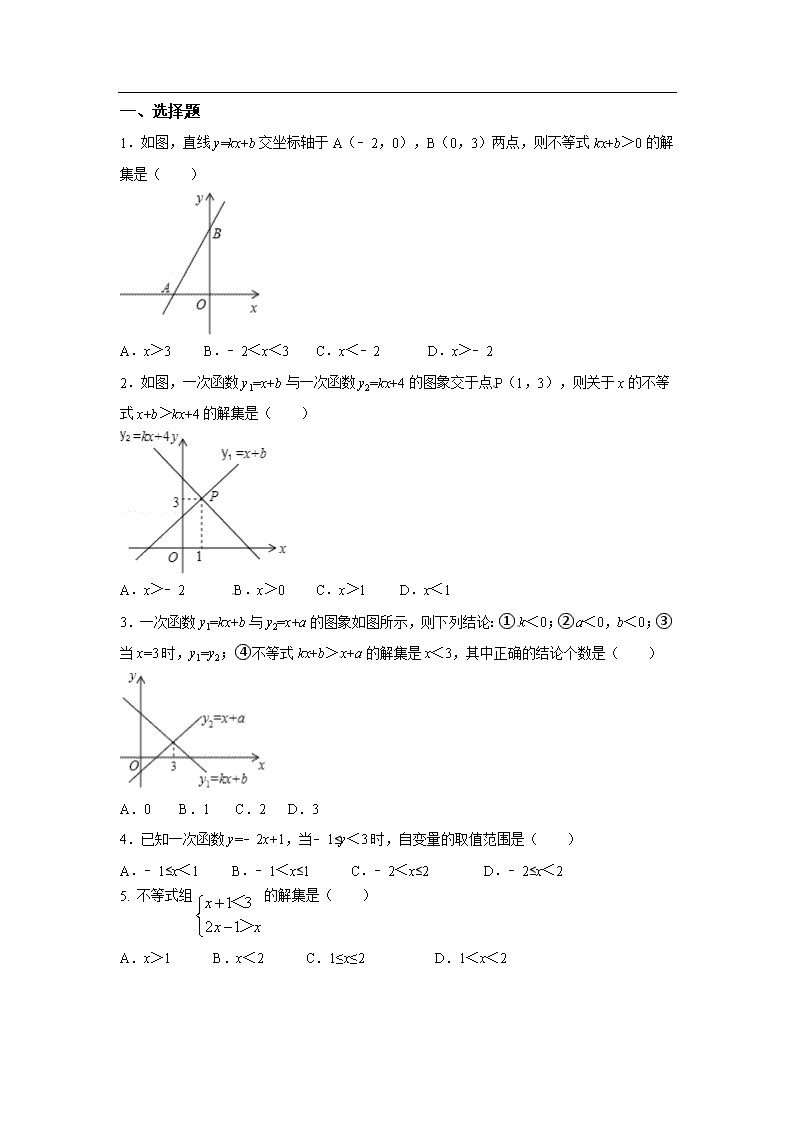
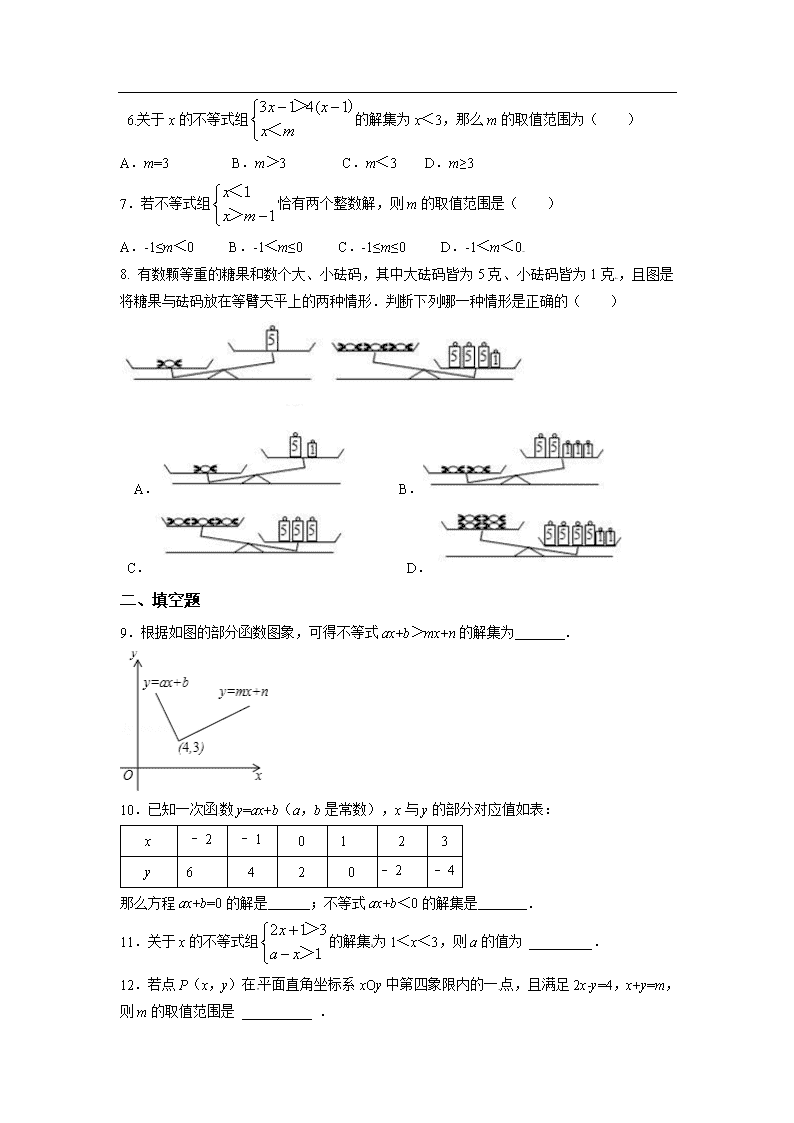
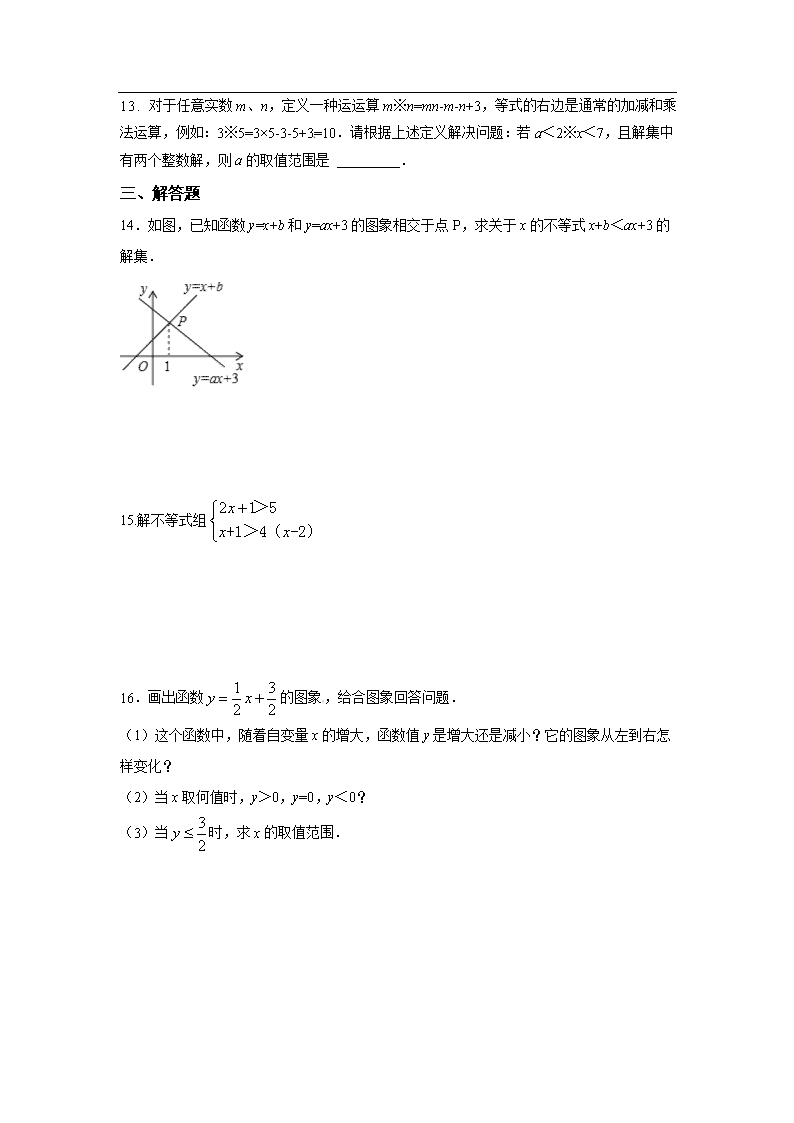
一、选择题 ‎1．如图，直线y=kx+b交坐标轴于A（﹣2，0），B（0，3）两点，则不等式kx+b＞0的解集是（　　）‎ A．x＞3 B．﹣2＜x＜3 C．x＜﹣2 D．x＞﹣2‎ ‎2．如图，一次函数y1=x+b与一次函数y2=kx+4的图象交于点P（1，3），则关于x的不等式x+b＞kx+4的解集是（　　）‎ A．x＞﹣2 B．x＞0 C．x＞1 D．x＜1‎ ‎3．一次函数y1=kx+b与y2=x+a的图象如图所示，则下列结论：①k＜0；②a＜0，b＜0；③当x=3时，y1=y2；④不等式kx+b＞x+a的解集是x＜3，其中正确的结论个数是（　　）‎ ‎[来源:学§科§网]‎ A．0 B．1 C．2 D．3‎ ‎4．已知一次函数y=﹣2x+1，当﹣1≤y＜3时，自变量的取值范围是（　　）‎ A．﹣1≤x＜1 B．﹣1＜x≤1 C．﹣2＜x≤2 D．﹣2≤x＜2[来源:学科网ZXXK]‎ ‎5. 不等式组的解集是（　　）‎ A．x＞1 B．x＜2 C．1≤x≤2 D．1＜x＜2‎ ‎6.关于x的不等式组的解集为x＜3，那么m的取值范围为（　　）‎ A．m=3 B．m＞3 C．m＜3 D．m≥3[来源:学#科#网Z#X#X#K]‎ ‎7．若不等式组恰有两个整数解，则m的取值范围是（　　）‎ A．-1≤m＜0 B．-1＜m≤0 C．-1≤m≤0 D．-1＜m＜0‎ ‎8. 有数颗等重的糖果和数个大、小砝码，其中大砝码皆为5克、小砝码皆为1克，且图是将糖果与砝码放在等臂天平上的两种情形．判断下列哪一种情形是正确的（　　）‎ ‎ A． B．‎ ‎ C． D．‎ 二、填空题 ‎9．根据如图的部分函数图象，可得不等式ax+b＞mx+n的解集为　 　．‎ ‎10．已知一次函数y=ax+b（a，b是常数），x与y的部分对应值如表：‎ x ‎﹣2‎ ‎﹣1‎ ‎0‎ ‎1[来源:学.科.网]‎ ‎2‎ ‎3‎ y ‎6[来源:学科网ZXXK]‎ ‎4‎ ‎2‎ ‎0‎ ‎﹣2[来源:学§科§网]‎ ‎﹣4‎ 那么方程ax+b=0的解是　 　；不等式ax+b＜0的解集是　 　．‎ ‎11．关于x的不等式组的解集为1＜x＜3，则a的值为 _________．‎ ‎12．若点P（x，y）在平面直角坐标系xOy中第四象限内的一点，且满足2x-y=4，x+y=m，则m的取值范围是 __________ ．‎ ‎13. 对于任意实数m、n，定义一种运运算m※n=mn-m-n+3，等式的右边是通常的加减和乘法运算，例如：3※5=3×5-3-5+3=10．请根据上述定义解决问题：若a＜2※x＜7，且解集中有两个整数解，则a的取值范围是 _________．‎ 三、解答题 ‎14．如图，已知函数y=x+b和y=ax+3的图象相交于点P，求关于x的不等式x+b＜ax+3的解集．‎ ‎15.解不等式组 ‎16．画出函数的图象，给合图象回答问题．‎ ‎（1）这个函数中，随着自变量x的增大，函数值y是增大还是减小？它的图象从左到右怎样变化？‎ ‎（2）当x取何值时，y＞0，y=0，y＜0？[来源:学#科#网Z#X#X#K]‎ ‎（3）当时，求x的取值范围．‎ ‎17．某中学为了绿化校园，计划购买一批榕树和香樟树，经市场调查榕树的单价比香樟树少20元，购买3棵榕树和2棵香樟树共需340元．‎ ‎（1）请问榕树和香樟树的单价各多少？‎ ‎（2）根据学校实际情况，需购买两种树苗共150棵，总费用不超过10840元，且购买香樟树的棵树不少于榕树的1.5倍，请你算算，该校本次购买榕树和香樟树共有哪几种方案．‎ ‎[来源:学科网]‎ ‎18．某汽车制造厂开发了一款新式电动汽车，计划一年生产安装240辆．由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人；他们经过培训后上岗，也能独立进行电动汽车的安装．生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车．‎ ‎（1）每名熟练工和新工人每月分别可以安装多少辆电动汽车？‎ ‎（2）如果工厂招聘n（0＜n＜10）名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种新工人的招聘方案？‎ ‎（3）在（2）的条件下，工厂给安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元的工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额W（元）尽可能地少？ ‎ 答案：‎ ‎1~5 DCDBD 6~8 DAD 9. x＜4 10.x=1 x＞1 11.4 12.-4＜m＜2 13.4≤a＜5‎ 14. 解：∵函数y=x+b和y=ax+3的图象相交于点P，P点横坐标为1， ∴不等式x+b＜ax+3的解集为：x＜1，‎ ‎15.解：解不等式2x+1＞5得x＞2，解不等式x+1＞4（x-2）得x＜3，[来源:学科网]‎ 所以不等式组的解集为2＜x＜3.‎ ‎16.解：如图所示： （1）根据图象可得随着自变量x的增大，函数值y增大，它的图象从左到右呈上升趋势； ‎ （2） 根据图象可得x＞-3时y＞0； x=-3时y=0， x＜-3时，y＜0；‎ 17. 解：（1）设榕树的单价为x元/棵，香樟树的单价是y元/棵，[来源:Zxxk.Com]‎ 答：榕树和香樟树的单价分别是60元/棵，80元/棵； （2）设购买榕树a棵，则购买香樟树为（150-a）棵，‎ 解不等式①得，a≥58， 解不等式②得，a≤60， 所以，不等式组的解集是58≤a≤60， ∵a只能取正整数， ∴a=58、59、60， 因此有3种购买方案： 方案一：购买榕树58棵，香樟树92棵， ‎ 方案二：购买榕树59棵，香樟树91棵， 方案三：购买榕树60棵，香樟树90棵．‎ 17. 解：（1）设每名熟练工和新工人每月分别可以安装x辆和y辆汽车，‎ 答：每名熟练工和新工人每月分别可以安装4辆和2辆汽车． （2）设需熟练工m名， 根据题意得：2n×12+4m×12=240， ∴n=10-2m． ∵0＜n＜10， ∴0＜m＜5． 当m=1时，n=8；当m=2时，n=6；当m=3时，n=4；当m=4时，n=2． ∴共有四种方案：①需要1名熟练工人，另招聘8名新工人；②需要2名熟练工人，另招聘6名新工人；③需要3名熟练工人，另招聘4名新工人；④需要4名熟练工人，另招聘2名新工人．‎ ‎∵要使新工人数量多于熟练工， ∴n=4、6、8． ∵200＞0， ∴当n=4时，W取最小值，最小值为10800．‎