北师大版数学初中八年级上册课件-第6章 复习课

北师大版数学初中八年级上册课件-第6章 复习课

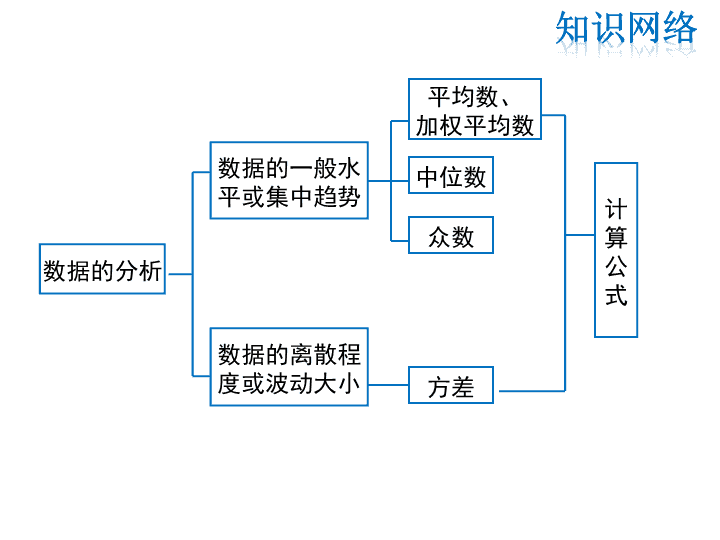
第六章数据的分析复习课 数据的分析数据的一般水平或集中趋势数据的离散程度或波动大小平均数、加权平均数中位数众数方差计算公式知识网络 数据的代表平均数定义一组数据的平均值称为这组数据的平均数算术平均数一般地，如果有n个数x1，x2，…，xn，那么叫做这n个数的平均数加权平均数一般地，如果在n个数x1，x2，…，xn中，x1出现f1次，x2出现f2次，…，xk出现fk次(其中f1＋f2＋…＋fk＝n)，那么，叫做x1，x2，…，xk这k个数的加权平均数，其中f1，f2，…，fk叫做x1，x2，…，xk的权，f1＋f2＋…＋fk＝n1知识梳理 最多中间位置的数两个数据的平均数中位数定义将一组数据按照由小到大(或由大到小)的顺序排列，如果数据的个数是奇数，则处于________________就是这组数据的中位数，如果数据的个数是偶数，则中间_________________________就是这组数据的中位数防错提醒确定中位数时，一定要注意先把整组数据按照大小顺序排列，再确定众数定义一组数据中出现次数________的数据叫做这组数据的众数防错提醒(1)一组数据中众数不一定只有一个；(2)当一组数据中出现异常值时，其平均数往往不能正确反映这组数据的集中趋势，就应考虑用中位数或众数来分析中间位置的数最多两个数据的平均数知识梳理 (2)条形统计图中，(3)扇形统计图中，(1)折线统计图中，众数：同一水平线上出现次数最多的数据；中位数：从上到下（或从下到上）找中间点所对的数；平均数：可以用中位数与众数估测平均数．众数：是柱子最高的数据；中位数：从左到右（或从右到左）找中间数；平均数：可以用中位数与众数估测平均数．众数：为扇形面积最大的数据；中位数：按顺序，看相应百分比，第50%与51%两个数据的平均数；平均数：可以利用加权平均数进行计算．从统计图中分析数据2知识梳理 数据的波动表示波动的量定义意义方差设有n个数据x1，x2，x3，…，xn，各数据与它们的______的差的平方分别是(x1－x)2，(x2－x)2，…，(xn－x)2，我们用它们的平均数，即用_____________________________来衡量这组数据的波动大小，并把它叫做这组数据的方差，记作s2方差越大，数据的波动越________，反之也成立平均数大标准差就是方差的算术平方根3知识梳理 1.下表是王勇家去年1-6月份的用水情况：则王勇家去年1-6月份的月平均用水量为（　　）A．3吨B．3.5吨C．4吨D．4.5吨C解析：（3+4+3.5+3+4.5+6）÷6=24÷6=4（吨）．故选C．随堂即练 2.某班体育委员统计了全班45名同学一周的体育锻炼时间，并绘制了如图所示的折线统计图，则在体育锻炼时间这组数据中，众数和中位数分别是（　　）A．18，18B．9，9C．9，10D．18，9B解析：由图可知，锻炼9小时的有18人，所以9在这组数中出现18次为最多，所以众数是9．把数据从小到大排列，中位数是第23位数，第23位是9，所以中位数是9．随堂即练 3.要反映台州市某一周每天的最高气温的变化趋势，宜采用()A.条形统计图B.扇形统计图C.折线统计图D.频数分布直方图C随堂即练 4.如图是某农户2015年收入情况的扇形统计图，已知他2015年的总收入为5万元，则他的打工收入是()A.0.75万元B.1.25万元C.1.75万元D.2万元B解析:5万元×25%=1.25万元.随堂即练 5.我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀．这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示，其中七年级代表队得6分、10分的选手人数分别为a，b.随堂即练 队别平均分中位数方差合格率优秀率七年级6.7m3.4190%n八年级7.17.51.6980%10%(1)请依据图表中的数据，求a，b的值；(2)直接写出表中m，n的值；(3)有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．随堂即练 (1)解：依题意，得解得3×1+6a+7×1+8×1+9×1+10b=6.7×10a+1+1+1+b=90％×10或1+a+1+1+1+b=10a=5b=1(1)请依据图表中的数据，求a，b的值；随堂即练 (2)m＝6，n＝20%.(2)直接写出表中m，n的值；队别平均分中位数方差合格率优秀率七年级6.7m3.4190%n八年级7.17.51.6980%10%随堂即练 (3)①八年级队平均分高于七年级队；②八年级队的成绩比七年级队稳定；③八年级队的成绩集中在中上游，所以支持八年级队成绩好．(注：任说两条即可)(3)有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．随堂即练 6.为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表：甲、乙射击成绩统计表平均数中位数方差命中10环的次数甲70乙1随堂即练 甲、乙射击成绩折线图(1)请补全上述图表(请直接在表中填空和补全折线图)；(2)如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；(3)如果希望(2)中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？随堂即练 解：(1)根据折线统计图，得乙的射击成绩为2，4，6，8，7，7，8，9，9，10，平均数为(环)中位数为7.5环，方差为[(2－7)2＋(4－7)2＋(6－7)2＋(8－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(9－7)2＋(9－7)2＋(10－7)2]＝5.4.根据折线统计图，知甲除第八次外的射击成绩为9，6，7，6，2，7，7，8，9，平均数为7，则甲第八次成绩为70－(9＋6＋7＋6＋2＋7＋7＋8＋9)＝9(环)，所以甲的射击成绩为2，6，6，7，7，7，8，9，9，9，随堂即练 中位数为7环，平均数为(2＋6＋6＋7＋7＋7＋8＋9＋9＋9)＝7(环)，方差为[(2－7)2＋(6－7)2＋(6－7)2＋(7－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(9－7)2＋(9－7)2＋(9－7)2]＝4.补全图表如下．甲、乙射击成绩统计表平均数中位数方差命中10环的次数甲7740乙77.55.41随堂即练 甲、乙射击成绩折线图(2)甲胜出．理由：因为甲的方差小于乙的方差．(3)略.随堂即练