2020秋八年级数学上册第12章一次函数12-2一次函数第4课时一次函数的应用—分段函数教学课件（新版）沪科版

2020秋八年级数学上册第12章一次函数12-2一次函数第4课时一次函数的应用—分段函数教学课件（新版）沪科版

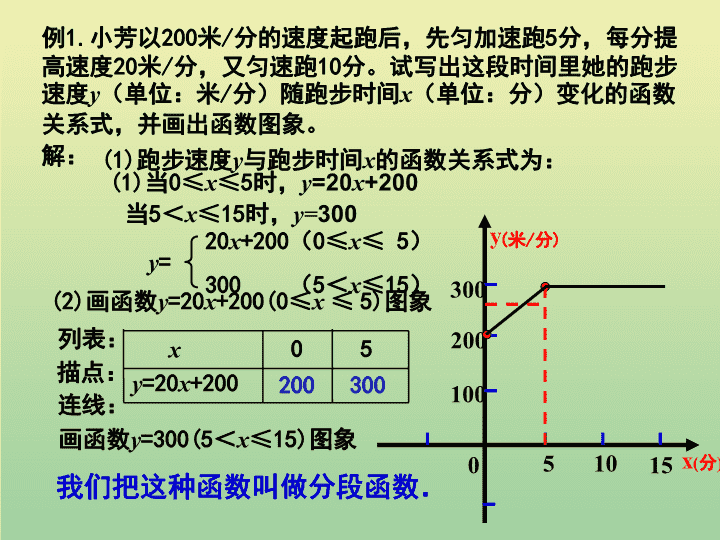
第4课时分段函数 分析：本题y随x变化的规律分成两段：前5分钟与后10分钟．写y随x变化函数关系式时要分成两部分．画图象时也要分成两段来画，且要注意各自变量的取值范围.例1.小芳以200米/分的速度起跑后，先匀加速跑5分，每分提高速度20米/分，又匀速跑10分。试写出这段时间里她的跑步速度y（单位：米/分）随跑步时间x（单位：分）变化的函数关系式，并画出函数图象。 例1.小芳以200米/分的速度起跑后，先匀加速跑5分，每分提高速度20米/分，又匀速跑10分。试写出这段时间里她的跑步速度y（单位：米/分）随跑步时间x（单位：分）变化的函数关系式，并画出函数图象。y=20x+200（0≤x≤5）300（5＜x≤15）(1)跑步速度y与跑步时间x的函数关系式为：010052003001015y(米/分)x(分)(2)画函数y=20x+200(0≤x≤5)图象xy=20x+20005列表：描点：连线：画函数y=300(5＜x≤15)图象200300我们把这种函数叫做分段函数．(1)当0≤x≤5时，y=20x+200当5＜x≤15时，y=300解： 分析：付款金额与种子价格相关，问题中的种子价格不是固定不变的，它与购买种子数量有关，设购买x千克种子，当0≤x≤2时，种子价格为5元/千克；当x＞2时，其中有2千克种子按5元/千克计算，其余的（x-2）千克（即超出2千克部分）种子按4元/千克（即8折）计价.因此，写函数解析式与画函数图像时，应对0≤x≤2和x＞2分段讨论.例2.“黄金1号”玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子的价格打8折.(1)填出下表：购买种子数量/千克0.511.522.533.54…付款金额/元…(2)写出购买种子数量与付款金额之间的函数解析式，并画出函数的图像.2.557.51012141816解：(1)填表；(2)设购买种子数量为x千克，付款金额为y元.当0≤x≤2时，y=5x.当x＞2时，y=4(x-2)+10即y=4x+2y与x的函数解析式也可合起来表示为y=5x（0≤x≤2）4x+2（x＞2） 051101523yx函数图像如图所示：y=5xy=4x+2 例3.为节约用水，某城市制定以下用水收费标准：每户每月用水不超过8m³时，每m³收取1元外加0.3元的污水处理费；超过8m³时，每m³收取1.5元外加1.2元的污水处理费.设一户每月用水量为xm³，应缴水费y元.①给出y与x之间的函数表达式；②画出上述函数图象；③当该市一户某月的用水量为5m³或10m³时，求其应缴的水费；④该市一户某月缴水费26.6元，求该户这个月用水量. 为了加强公民的节水意识,某城市规定用水收费标准如下:每户每月用水量不超过6米3时,水费按0.6元/米3收费,超过6米3时,超过部分每米3按1元收费,每户每月用水量为x米3,应缴水费y元.试金石(1)写出每月用水量不超过6米3和超过6米3时,y与x之间的函数关系式.(2)已知某户5月份用水量为8米3，求该用户5月份的水费。解：(1)当0≤x≤6时，y=0.6x.当x＞6时，y=0.6×6+1×(x-6)即y=x-2.4(2)当x=8时，y=8-2.4=5.6故,该用户5月份的水费为5.6元. （3）数学与生活、生产实际有密切联系，我们碰到实际问题要善于用数学方法去分析、去解决，看到数学的函数图像也要善于给它赋予不同的意义，这是学好数学的秘诀之一。（1）识别、分析函数图像所描述的信息；（2）把简单的实际问题转化为数学问题（函数模型）；利用数学方法来解决有关实际问题；现实问题数学化数学问题(模型)数学方法数学问题的解还原说明现实问题的解。收获乐园驶向胜利的彼岸 2.某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药（1）服药后____时，血液中含药量最高,达到每毫升_______毫克。（2）服药5时，血液中含药量为每毫升____毫克。（3）当x≤2时,y与x之间的函数关系式是_____。（4）当x≥2时,y与x之间的函数关系式是_________。（5）如果每毫升血液中含药量3毫克或3毫克以上时，治疗疾病最有效，那么这个有效时间是___小时。.x/时y/毫克6325O能力提升2263y=3xy=-x+84点评（1）根据图像反映的信息解答有关问题时，首先要弄清楚两坐标轴的实际意义，抓住几个关键点来解决问题；（2）特别注意，第5问中由y=3对应的x值有两个；（3）根据函数图像反映的信息来解答有关问题，比较形象、直观，从中能进一步感受“数形结合思想”。 某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药的一定时间内每毫升血液中含药量y（微克）随时间x（时）逐步增加,变化情况如图所示.62Ox/时y/微克（1）当0≤x≤2时,y与x之间的函数关系式是。y=3x拓展提高 62Ox/时y/微克（3）如果每毫升血液中含药量4微克或4微克以上时在治疗疾病是有效的，那么这个有效时间是多长?4（2）服药后2时，血液中含药量最高达每毫升6微克，接着每小时逐步衰减微克。求出当x≥2时y与x之间的函数关系式.6