八年级下数学课件八年级下册数学课件《直角三角形》 北师大版 (7)_北师大版

八年级下数学课件八年级下册数学课件《直角三角形》 北师大版 (7)_北师大版

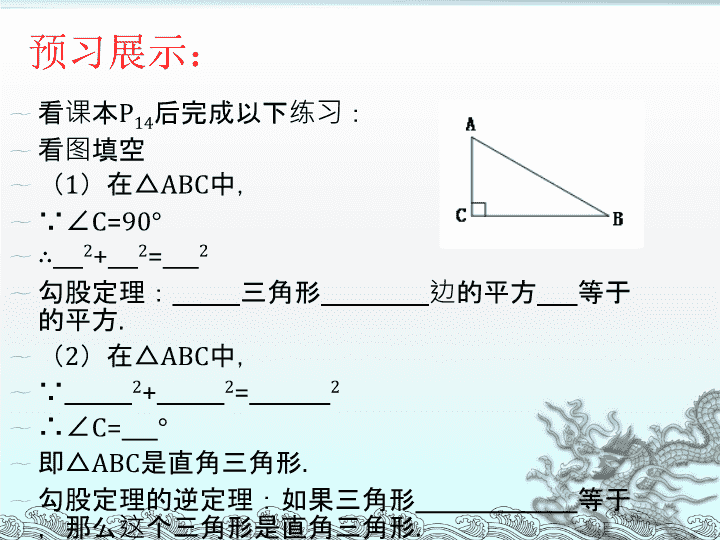
第一章三角形的证明2.直角三角形（一）北师大版八年级下册 学习目标：1.掌握直角三角形的性质定理（勾股定理）及判定定理的证明方法，并能应用定理解决与直角三角形有关的问题；2.结合具体例子了解逆命题的概念，会识别两个互逆命题，知道原命题成立，其逆命题不一定成立；3.进一步掌握推理证明的方法，发展演绎推理的能力． 看课本P14后完成以下练习：看图填空（1）在△ABC中，∵∠C=90°∴2+2=2勾股定理：三角形边的平方等于的平方.（2）在△ABC中，∵2+2=2∴∠C=°即△ABC是直角三角形.勾股定理的逆定理：如果三角形等于，那么这个三角形是直角三角形.预习展示： 新课讲解例1.已知：在△ABC中，AB2+AC2=BC2.求证：△ABC是直角三角形.定理：如果三角形两边的______等于，那么这个三角形是直角三角形. 2.阅读课本P15－16页“想一想”，回答下列问题：(1)一个命题是真命题，那么它的逆命题也一定是真命题吗？(2)什么是互逆定理？(3)是否任何定理都有逆定理？(4)思考我们学过哪些互逆定理？ 观察下面三组命题：学生以分组讨论形式进行，最后在教师的引导下得出命题与逆命题的区别与联系。如果两个角是对顶角，那么它们相等．如果两个角相等，那么它们是对顶角．如果小明患了肺炎，那么他一定发烧．如果小明发烧，那么他一定患了肺炎．三角形中相等的边所对的角相等．三角形中相等的角所对的边相等．上面每组中两个命题的条件和结论也有类似的关系吗?与同伴交流．议一议 在两个命题中，如果一个命题条件和结论分别是另一个命题的结论和条件，那么这两个命题称为互逆命题，其中一个命题称为另一个命题的逆命题，相对于逆命题来说，另一个就为原命题． 由此我们可以发现：原命题是真命题，而逆命题不一定是真命题．再来看“议一议”中的三组命题，它们就称为互逆命题，如果称每组的第一个命题为原命题，另一个则为逆命题．请同学们判断每组原命题的真假．逆命题呢? 如果有些命题，原命题是真命题，逆命题也是真命题，那么我们称它们为互逆定理.其中逆命题成为原命题（即原定理）的逆定理．想一想请写出命题“如果两个有理数相等，那么它们的平方相等”的逆命题吗?它们都是真命题吗？你能举例说出我们已学过的互逆定理吗? 课堂检测1.判断题（1）每个命题都有逆命题，每个定理也都有逆定理.（）（2）命题正确时其逆命题也正确.（）（3）直角三角形两边分别是3，4，则第三边为5.（）2.以下命题的逆命题属于假命题的是（）A.两底角相等的两个三角形是等腰三角形.B.全等三角形的对应角相等.C.两直线平行，内对角相等.D.直角三角形两锐角互等.3.写出下列命题的逆命题，并判断每对命题的真假：（1）五边形是多边形.（2）两直线平行，同位角相等.（3）如果两个角是对顶角，那么它们相等.（4）如果ab=0，那么a=0，b=0.4.公园中景点A、B间相距50M，景点A、C间相距40M，景点B、C间相距30M，由这三个景点构成的三角形一定是直角三角形吗？为什么？ 这节课我们了解了勾股定理及逆定理的证明方法，并结合数学和生活中的例子了解逆命题的概念，会识别两个互逆命题，知道，原命题成立，其逆命题不一定成立，掌握了证明方法，进一步发展了演绎推理能力．课时小结 课后作业习题1.5第1、2、3题