八年级下数学课件：18-2-1 矩形 （共26张PPT）_人教新课标

八年级下数学课件：18-2-1 矩形 （共26张PPT）_人教新课标

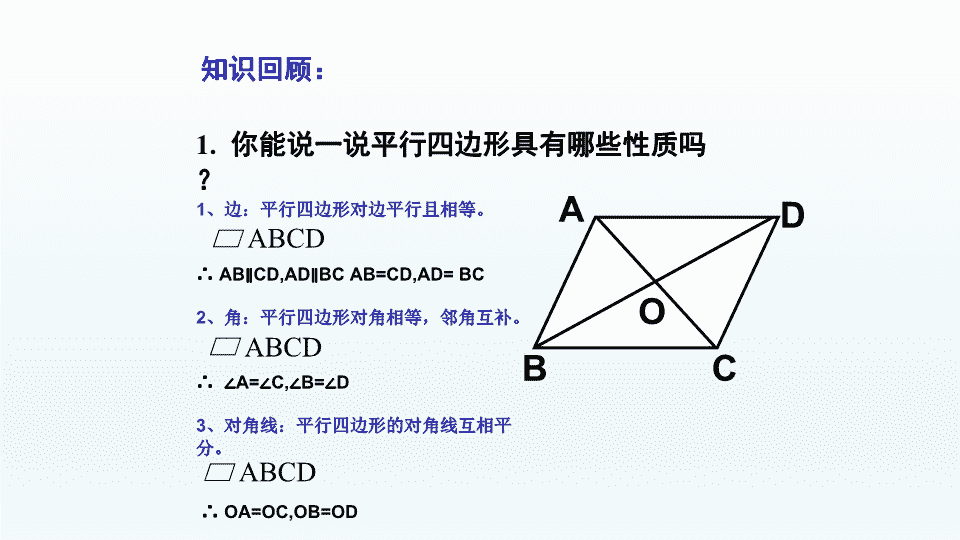
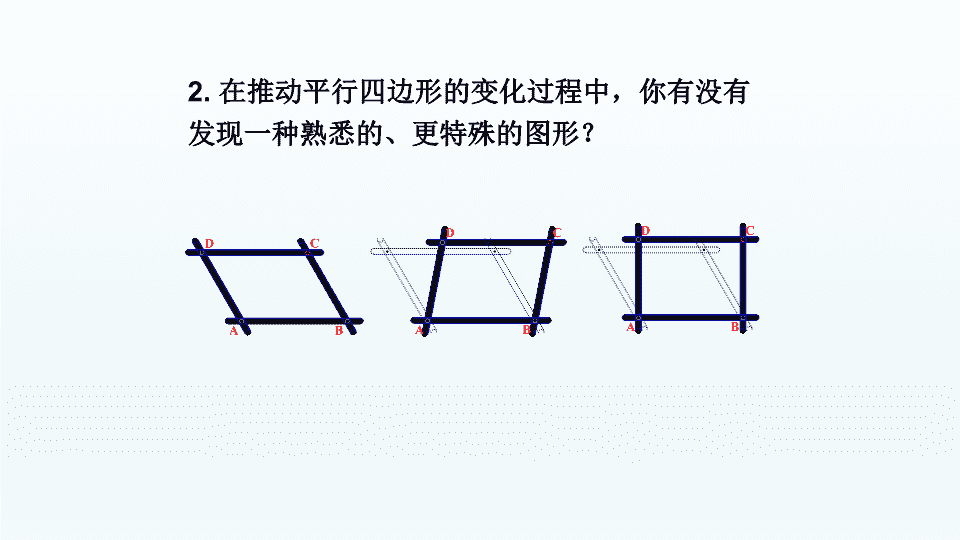
18.2.1矩形18.2特殊的平行四边形 知识回顾：1.你能说一说平行四边形具有哪些性质吗？ABCDO1、边：平行四边形对边平行且相等。∴AB∥CD,AD∥BCAB=CD,AD=BC2、角：平行四边形对角相等，邻角互补。∴∠A=∠C,∠B=∠D3、对角线：平行四边形的对角线互相平分。∴OA=OC,OB=ODABCDABCDABCD 2.在推动平行四边形的变化过程中，你有没有发现一种熟悉的、更特殊的图形？ 定义：有一个角是直角的平行四边形叫做矩形。BACDABCD有一个直角 思考:作为特殊的平行四边形，矩形具有平行四边形的所有性质外，还有哪些特殊性质呢？结论1：矩形的四个角都是直角．结论2：矩形的对角线相等．ABCD 证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;(6)检查表达过程是否正确,完善.学好几何的标志是会“证明” 矩形的性质命题:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,∠B=1800-∠A=900,∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴∠A=∠B=∠C=∠D=900DBCA性质1 已知：四边形ABCD是矩形，求证：AC=BDABCD证明：在矩形ABCD中有∠ABC=∠DAB=90°BC=AD又∵AB=BA∴△ABC≌△BAD∴AC=BD2：矩形的对角线相等．命题性质 边角对角线平行四边形矩形对边平行且相等对角相等邻角互补对角线互相平分对边平行且相等四个角都是直角对角线互相平分且相等类比总结矩形特有的性质 公平,因为OA=OC=OB=OD四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处，目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么？OABCD生活链接---投圈游戏 ODCBA┛在Rt△ABD中，AO是斜边BD的中线直角三角形的性质：直角三角形斜边上的中线等于斜边的一半。则有：AO=BD试试：用文字叙述直角三角形的性质在矩形ABCD中AO=CO=BO=DO==思考:在Rt△ABD中，AO和BD是什么关系?ACBD 请选择624351挑战第一关进入第二关进入第三关通关小结（快速问答） 1、矩形的定义中有两个条件：一是：二是：。。有一个角是直角一定是平行四边形 2、矩形具有而一般平行四边形不具有的性质是（）（A）对角线相等（B）对边相等（C）对角相等（D）对角线互相平分A 4、在Rt△ABC中，∠ABC=90°，AC=14，BO是斜边上的中线，则BO的长为ACBO。7 3、如图，在矩形ABCD中，对角线AC、BD相交于点O，且AB=3,BC=4，则△ABO的周长为ABCDO。8（小组讨论完成后汇报。时间：1分钟） 5、矩形是轴对称图形吗?它的对称轴是什么？是对边中点连线所在的直线 练习：如图，矩形ABCD的两条对角线相交于点O，且∠AOB=60°，AB=4cm．求矩形对角线的长．ABCDO解：∵四边形ABCD是矩形，∴AC与BD相等且互相平分。∴OA=OB.又∠AOB=60°，∴△OAB是等边三角形。∴OA=AB=4.∴AC=BD=2AO=8.挑战第二关：运用性质　解决问题 练习：如图，在矩形ABCD中，AE平分∠BAD,交BC于点E,ED=5，EC=3,求矩形的周长及对角线的长。ABCDE354447挑战第三关 谈谈你在这节课中学到了什么？有哪些收获？课堂小结 直角三角形性质：直角三角形斜边上的中线等于斜边的一半．矩形是轴对称图形，有两条对称轴。课堂小结矩形1、具有平行四边形的所有性质；2、矩形的四个角都是直角；3、矩形的对角线相等且互相平分．矩形：有一个角是直角的平行四边形叫做矩形． 作业：完成课时练作业课后作业 学习提示：条理清晰，因果相应,言必有据，是初学证明者谨记和遵循的原则.