八年级上数学课件- 14-3-1 提公因式法 课件（共20张PPT）_人教新课标

八年级上数学课件- 14-3-1 提公因式法 课件（共20张PPT）_人教新课标

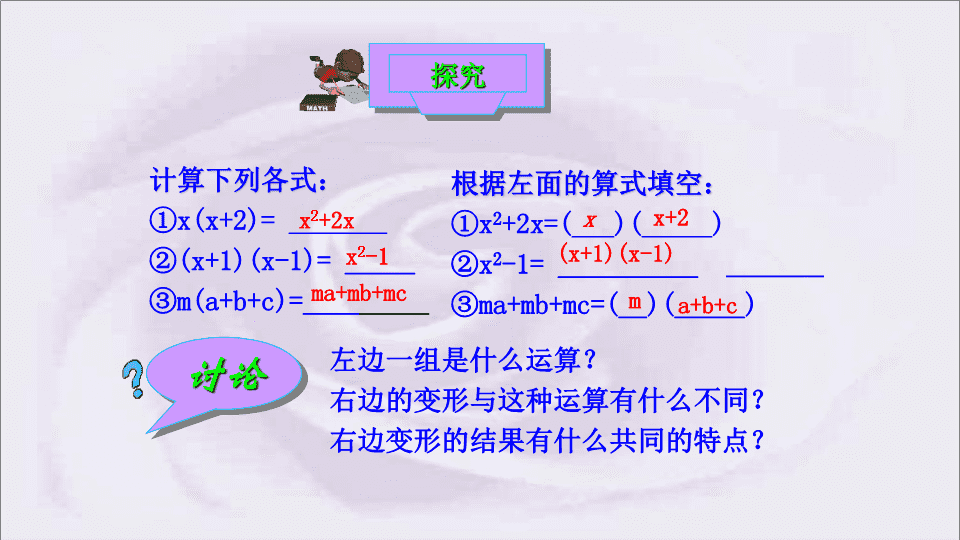
14.3.1提公因式法分解因式 1.把下列各数写成质数的乘积的形式：（1）36=________________（2）63=__________________（2）解：63=3²×7（1）解：36=2²×3²思考 根据左面的算式填空：①x2+2x=(___)(_____)②x2-1=__________③ma+mb+mc=(__)(_____)计算下列各式：①x(x+2)=_______②(x+1)(x-1)=_____③m(a+b+c)=_________x2+2xma+mb+mcxx+2ma+b+c左边一组是什么运算？右边的变形与这种运算有什么不同？右边变形的结果有什么共同的特点？探究讨论(x+1)(x-1)x2-1 从类比中你能发现什么……a(m+n)=am+anam+an=a(m+n)整式的乘法它的逆过程互逆思想 把一个多项式化成了几个整式的积的形式，像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式。因式分解整式乘法因式分解与整式乘法是逆变形 判断下列各式哪些是整式乘法?哪些是因式分解(1)x2－4y2=(x+2y)(x－2y)；(2)2x(x－3y)=2x2－6xy(3)(5a－1)2=25a2－10a+1；(4)x2+4x+4=(x+2)2；(5)(a－3)(a+3)=a2－9(6)m2－4=(m+2)(m－2)；因式分解整式乘法整式乘法因式分解整式乘法因式分解【跟踪训练】分析：因式分解概念的方法技巧：“多项式（和）→乘积的形式”，在判断一个式子是否是因式分解时，利用这一方法，可以粗略地判断出选项． 学校打算把操场重新规划一下，分为绿化带、运动场、主席台三个部分，如下图，计算操场总面积。abcm方法一：S=m(a+b+c)方法二：S=ma+mb+mc m(a+b+c)=ma+mb+mc下面两个式子中哪个是因式分解？在式子ma+mb+mc中，它的各项都有一个公共的因式m，因式m叫做这个多项式的公因式。ma+mb+mc=m(a+b+c) ma+mb+mc=m(a+b+c)在下面这个式子的因式分解过程中，先找到这个多项式的公因式，再将原式除以公因式，得到一个新多项式，将这个多项式与公因式相乘即可。这种方法叫做提公因式法。提公因式法一般步骤：1、找到该多项式的公因式，2、将原式除以公因式，得到一个新多项式，3、把它与公因式相乘。 8a3b2－12ab3c的公因式是什么？最大公约数相同字母公因式4a,bab2一看系数观察方向二看字母三看指数相同字母的最低指数确定公因式的方法：(1)定系数(2)定字母(3)定指数公因式为：4ab2找公因式技巧：先系数，大公约；同部分，幂最低 【例1】把8a3b2+12ab3c分解因式.【解析】8a3b2+12ab3c=4ab2•2a2+4ab2•3bc=4ab2(2a2+3bc).反思:Ⅰ.提取公因数后,括号内的多项式的项数与原多项式的项数相同.Ⅱ.利用整式的乘法来检验因式分解是否正确.2、提公因式法分解因式步骤(分两步)：第一步，找出公因式；第二步，提取公因式. 课堂练习1.说出下列多项式各项的公因式,（并将它们进行分解因式.）（1）ax+ay-a；（3）2a²x-3ax²；（4）12xyz-9x²y²；（5）2a(b+c)-3(b+c)（2）3a²+12ab；a3aax3xy(b+c)提公因式法分解因式应注意的问题：（1）公因式要提尽；（2）某项完全提出莫漏1;（3）提出负号时,要注意变号.记住哟！ 解：原式=a（x－3）+2b（x－3）=(x－3)(a+2b).例2把a（x－3）+2b（x－3）分解因式.分析：这个多项式整体而言可分为两大项，即a(x－3)与2b(x－3)，每项中都含有（x－3）,因此可以把(x－3)作为公因式提出来. 变式.分解因式:（1）a（x－y）+b（y－x）（2）3(a+b)²-6(a+b)；（3）6（m－n）3－12（n－m）2分析：虽然a（x－y)与b(y－x)看上去没有公因式，但仔细观察可以看出（x－y)与(y－x）互为相反数，如果把其中一个提取一个“－”号，则可以出现公因式，如：y－x=－（x－y）【解析】a（x－y）+b（y－x）=a（x－y）－b（x－y）=（x－y）（a－b）. 解：3(a+b)²-6(a+b)=3(a+b)2－2［3(a+b)］=3(a+b)（a+b－2）.（2）3(a+b)²-6(a+b)（3）6（m－n）3－12（n－m）2解：6（m－n）3－12（n－m）2=6（m－n）3－12［－（m－n）］2=6（m－n）3－12（m－n）2=6（m－n）2（m－n－2）. 例3把－x3＋x2－x分解因式．多项式的第一项是系数为负数的项，一般地，应提出负系数的公因式．但应注意，这时留在括号内的每一项的符号都要改变，且最后一项“－x”提出时，应留有一项“＋1”，而不能错解为－x(x2－x)．解：原式＝－(x3－x2＋x)＝－x(x2－x＋1)注意 1.一般地，如果多项式的各项有公因式，可以把这个公因式提取出来，将多项式写成公因式与另一个因式的乘积的形式，这种分解因式的方法叫做提公因式法.提公因式法2.分解因式的方法：注意符号变化通过本课时的学习，需要我们掌握：３.利用整式的乘法来检验因式分解是否正确. 2、确定公因式的方法：3、提公因式法分解因式步骤(分两步)：1、什么叫因式分解？(1)定系数(2)定字母(3)定指数第一步，找出公因式；第二步，提取公因式.4、提公因式法分解因式应注意的问题：（1）公因式要提尽；（2）某项提出莫漏1;（3）提出负号时,要注意变号.记住哟！ 1.把下列各式分解因式（1）3x²-6xy+x（2）a2b－5ab（3）21a²+7a（4）2a(y-z)-3b(z-y)；（5）－a2+ab－ac=x（3x－2y+1）=ab（a－5）=7a（3a+1）=(y-z)（2a+3b）=－（a2－ab+ac）=－a（a－b+c）2.先分解因式，再求值：4a²(x+7)-3(x+7)，其中a=-5，x=3.解：原式=(x+7)(4a²-3)当a=-5，x=3时，原式=（3+7）×（100-3）=10×97=970 海阔凭鱼跃，天高任鸟飞.