八年级下数学课件《三角形的中位线》课件4_冀教版

八年级下数学课件《三角形的中位线》课件4_冀教版

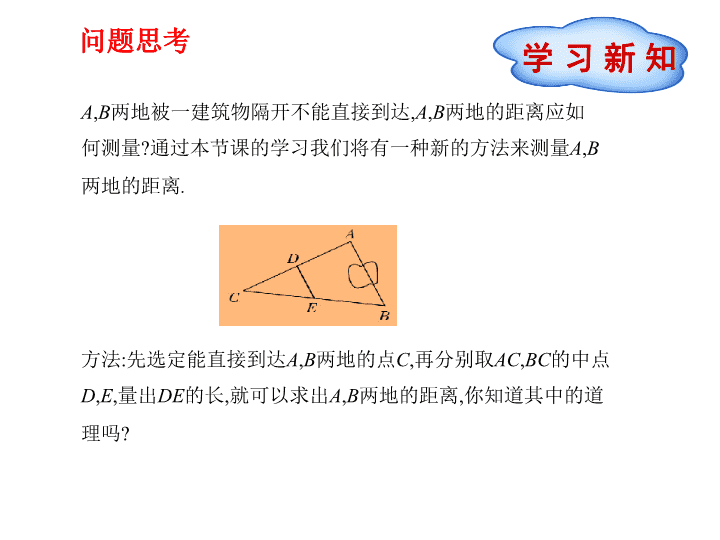
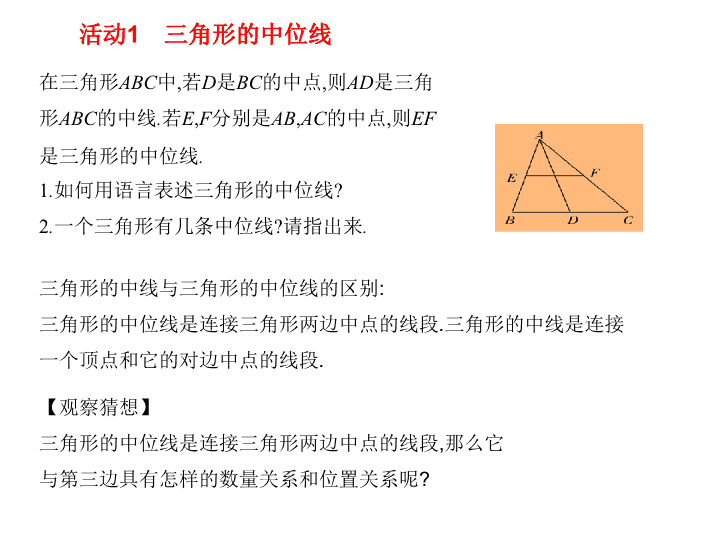
八年级数学·下新课标[冀教]第二十二章四边形22.3三角形的中位线 学习新知问题思考A,B两地被一建筑物隔开不能直接到达,A,B两地的距离应如何测量?通过本节课的学习我们将有一种新的方法来测量A,B两地的距离.方法:先选定能直接到达A,B两地的点C,再分别取AC,BC的中点D,E,量出DE的长,就可以求出A,B两地的距离,你知道其中的道理吗? 活动1三角形的中位线在三角形ABC中,若D是BC的中点,则AD是三角形ABC的中线.若E,F分别是AB,AC的中点,则EF是三角形的中位线.1.如何用语言表述三角形的中位线?2.一个三角形有几条中位线?请指出来.三角形的中线与三角形的中位线的区别:三角形的中位线是连接三角形两边中点的线段.三角形的中线是连接一个顶点和它的对边中点的线段.【观察猜想】三角形的中位线是连接三角形两边中点的线段,那么它与第三边具有怎样的数量关系和位置关系呢? 如图所示,DE为△ABC的中位线,DE与BC具有怎样的数量关系和位置关系呢?方法一(测量法):1.任意画一个三角形并画出它的一条中位线.2.分别量出中位线和第三边的长度.3.量出所画图形中一组同位角的度数.4.你发现了什么?方法二(裁剪拼接法):1.剪一个三角形,记作△ABC.2.分别找到边AB和AC的中点D,E,连接DE.3.沿DE把△ABC剪成两部分.4.把剪成的两部分图形重新拼接.5.新拼接的四边形是什么特殊的四边形? 拼接的过程如图所示,将△ADE绕点E旋转180°后得到△CFE,于是拼接成四边形BCFD,那么四边形BCFD是什么特殊的四边形呢?试着说明理由.思考:DE与BC之间的位置关系和数量关系是怎样的?三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半. 图所示,在△ABC中,D,E,F分别是AB,BC,AC的中点,AC=12,BC=16.求四边形DECF的周长.分析:可由三角形的中位线定理得到DF∥EC,DE∥FC,从而证出四边形DECF是平行四边形,然后根据平行四边形的性质求解.解:∵D,E,F分别是AB,BC,AC的中点,∴DF∥EC,DE∥FC,∴四边形DECF是平行四边形,∴CE=DF=BC=8,CF=DE=AC=6,∴所求四边形DECF的周长为28. (教材第131页例题)已知:如图所示,在四边形ABCD中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点.求证△PMN是等腰三角形.分析:要证△PMN是等腰三角形就是要证三条边中有两条边相等,可借助三角形的中位线定理进行证明.证明:在△ABD中,∵N,P分别为AB,BD的中点,∴PN=AD.同理PM=BC.又∵AD=BC,∴PN=PM.∴△PMN是等腰三角形. 分析:因为四边形的对角线可以把四边形分成两个三角形,所以连接AC或BD,构造利用“三角形的中位线定理”的基本图形后,此题便可得证.已知:如图所示,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,求证四边形EFGH是平行四边形.证明:连接AC(如图所示),∵G,H分别是CD,DA的中点,∴HG∥AC,HG=AC(三角形的中位线定理).同理EF∥AC,EF=AC.∴HG∥EF,且HG=EF.∴四边形EFGH是平行四边形.【结论】顺次连接四边形四条边的中点,所得的四边形是平行四边形. 检测反馈1.(2016·厦门中考)如图所示,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,则下列结论正确的是()A.EF=CFB.EF=DEC.CFDE解析:∵DE是△ABC的中位线,∴E为AC的中点,∴AE=EC.∵CF∥BD,∴∠ADE=∠F.在△ADE和△CFE中,∴△ADE≌△CFE(AAS),∴DE=FE.故选B.B 2.(2016·河南中考)如图所示,在△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC交AB于点E,则DE的长为()A.6B.5C.4D.3解析:∵在Rt△ACB中,∠ACB=90°,AC=8,AB=10,∴BC=6.又∵DE垂直平分AC交AB于点E,∴DE是△ACB的中位线,∴DE=BC=3.故选D.D 3.(2016·陕西中考)如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为()A.7B.8C.9D.10解析:在Rt△ABC中,∵∠ABC=90°,AB=8,BC=6,∴AC==10,∵DE是△ABC的中位线,∴DE∥BM,DE=BC=3,∴∠EFC=∠FCM.∵∠FCE=∠FCM,∴∠EFC=∠ECF,∴EC=EF=AC=5,∴DF=DE+EF=3+5=8.故选B.B 4.如图所示,平行四边形ABCD中,AD=10,点P为BC上任意一点,分别连接AP,DP,E,F,G,H分别为AB,AP,DP,DC的中点,则EF+GH的值为()A.10B.5C.2.5D.无法确定解析:在平行四边形ABCD中,BC=AD=10.∵E,F,G,H分别为AB,AP,DP,DC的中点,∴EF是△ABP的中位线,GH是△DPC的中位线,∴EF+GH=BP+PC=BC=5.故选B.B 5.如图所示,等边三角形ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.(1)求证DE=CF;(2)求EF的长.解析:(1)直接利用三角形的中位线定理得出DE=BC,进而得出DE=FC;(2)利用平行四边形的判定与性质得出DC=EF,进而利用等边三角形的性质以及勾股定理求出EF的长.证明:(1)∵D,E分别为AB,AC的中点,∴DE∥BC,且DE=BC.∵延长BC至点F,使CF=BC,∴DE∥FC,即DE=CF.解:(2)∵DE∥FC,∴四边形DEFC是平行四边形,∴DC=EF.∵D为AB的中点,AB=2,∴AD=BD=1,CD⊥AB.在Rt△CBD中,BC=2,∴DC=EF= 6.在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过点D作DE∥AC,交AB于E.(1)求证AE=DE;(2)若AB=8,求线段DE的长.解析:(1)欲证明AE=DE,只需证明∠EAD=∠EDA;(2)证明DE为直角三角形ABD斜边的中线,即可解决问题.证明:(1)∵AD平分∠BAC,∴∠EAD=∠CAD.∵DE∥AC,∴∠EDA=∠CAD,∴∠EAD=∠EDA,∴AE=DE.解:(2)由(1)知,∠EAD=∠EDA.∵BD⊥AD,∴∠EBD+∠EAD=∠BDE+∠EDA=90°,∴∠EBD=∠BDE,∴DE=BE.又由(1)知AE=DE,∴DE=AB=×8=4. 7.如图所示,在△ABC中,AB=4,AC=3,AD,AE分别是△ABC的角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,求线段EF的长.解析:首先证明△AGF≌△ACF,则AG=AC=3,GF=CF,证得EF是△BCG的中位线,由三角形的中位线定理即可求解.解:∵AD是△ABC的角平分线,∴∠GAF=∠CAF.在△AGF和△ACF中,∴△AGF≌△ACF,∴AG=AC=3,GF=CF.∴BG=AB-AG=4-3=1.又∵AE是△ABC的中线,∴BE=CE,∴EF是△BCG的中位线,∴EF=BG=. 8.已知直角三角形ABC中,∠B=90°,AB=8,BC=6,BM为中线,△BMN为等腰三角形(点N在AB边或AC边上,且不与顶点重合),求S△BMN.解析:先根据勾股定理求得AC的长,然后根据直角三角形斜边上的中线等于斜边的一半,得BM=AC=5,通过作辅助线利用三角形的面积公式求解.解:在直角三角形ABC中,AC==10.∵BM为中线,∴BM=CM=AM=AC=5.当N在AB边上时,且BM=BN=5,过点M作MG⊥AB于点G.∵M是AC的中点,且MG∥BC,∴MG是△ABC的中位线,∴MG=BC=×6=3,=BN·MG=×5×3=.当N在AC边上时,过点B作BD⊥AC于点D,则BD==4.8.在直角三角形BMD中,DM==1.4.则=BD·DM=×4.8×1.4=3.36.∵△BMN是等腰三角形, 9.如图所示,在△ABC中,AB,BC,CA的中点分别是E,F,G,AD是高.求证∠EDG=∠EFG.解析:先连接EG,构造三角形的中位线,借助证明△EFG≌△GDE,即可得出结论.证明:连接EG,∵E,F,G分别是AB,BC,CA的中点,∴EF为△ABC的中位线,EF=AC.又∵AD是高,∴AD⊥BC,∴∠ADC=90°.∴DG为直角三角形ADC斜边上的中线,∴DG=AC.∴DG=EF.同理DE=FG.∵EG=GE,∴△EFG≌△GDE(SSS),∴∠EDG=∠EFG.