八年级上数学课件- 14-2-1 平方差公式 课件（共21张PPT）_人教新课标

八年级上数学课件- 14-2-1 平方差公式 课件（共21张PPT）_人教新课标

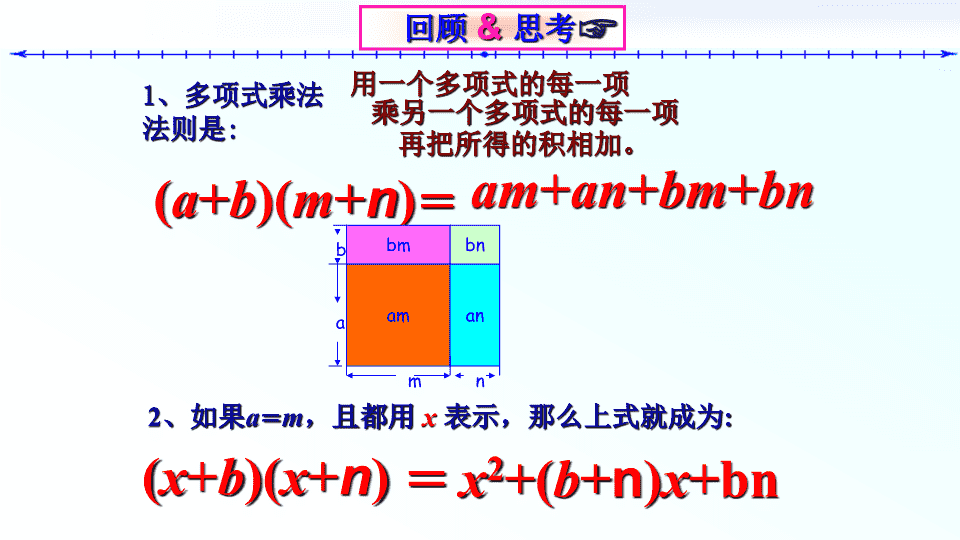
第十五章整式平方差公式 圣诞糖果圣诞即将来临，王敏捷同学去商店买了单价9.8元/千克的糖果10.2千克，售货员刚拿起计算器。王敏捷就说出应付99.96元。结果与售货员计算出的结果相吻合。售货员很惊讶得说：“你好象是个神童，你怎么算得这么快？”王敏捷同学说：“过奖了，我利用了在数学课上刚学过的一个公式。”你知道王敏捷用的什么公式吗？ 回顾与思考回顾&思考☞(a+b)(m+n)=2、如果a=m，且都用x表示，那么上式就成为:1、多项式乘法法则是:用一个多项式的每一项乘另一个多项式的每一项再把所得的积相加。am+an+bm+bn=(x+b)(x+n)x2+(b+n)x+bnamanbmbnmnab 平方差公式计算下列各题:做一做(1)(x+3)(x−3)；(2)(1+2a)(1−2a)；(3)(x+4y)(x−4y)；(4)(y+5z)(y−5z)；=x2−9;=1−4a2;=x2−16y2;=y2−25z2;观察&发现1、观察等式左边的两个二项式有什么特点？你发现了什么？用自己的语言叙述你的发现。=x2−32;=12−(2a)2;=x2−(4y)2;=y2−(5z)2.(a+b)(a−b)=a2−b2.两数和与这两数差的积,等于这两数的平方的差.用式子表示，即：2、观察等式右边的多项式; 有一位狡猾的地主，把一块边长为a米的正方形土地，租给李老汉种植。今年，他对李老汉说：“我把你这块地的一边减少4米，另一边增加4米，继续租给你，你也没有吃亏，你看如何？”李老汉一听，觉得好像没有吃亏，就答应了。同学们，你们觉得李老汉有没有吃亏？增加4aaaaaaa4减少(a-4)（a+4）a2-42= 平方差公式：平方差公式的图形理解aaa²bb2bb(a-b)（a+b）a2-b2a2-b2= 平方差公式：平方差公式的图形理解aaa²bb2b1/2(a-b)(a+b)×2a2-b2a2-b2=(a-b)（a+b） 学一学(2)(b+2a)(2a−b)=b2−()22a=4a2−b2;(a+b)(a-b)=(a)2-(b)2解(1)(3x+2)(3x-2)=(3x)2=9x2-4(a+b)(a-b)=a2-b2(2a+b)(2a−b)=例1利用平方差公式计算：(1)(3x+2)(3x−2)；(2)(b+2a)(2a−b);(2)2− 拓展练习本题是公式的变式训练，以加深对公式本质特征的理解．运用平方差公式计算：(4a1)(4a1)．运用平方差公式时，要紧扣公式的特征，找出相等的“项”和符号相反的“项”，然后应用公式．法一利用加法交换律，变成公式标准形式。(4a−1)(4a−1)==(1)2−(4a)2=1−16a2提取两“−”号中的“−”号，变成公式标准形式。法二(4a−1)(4a−1)=(4a+1)(4a−1)(4a−1)=(4a)2−1−计算时千万别忘了你提出的“”号、添括号；注意[]=1−16a2(4a−1)(4a−1)−1−4a−1+4a(4a+1)(4a−1) 纠错练习(1)(1+2x)(1−2x)=1−2x2(2)(2a2−b2)(−2a2−b2)=4a4−b4(3)(−3m+2n)(−3m−2n)=−9m2−4n2本题是对公式的直接运用，以加深对公式本质特征的理解．指出下列计算中的错误： 随堂练习(1)(a+3b)(a−3b)；(2)(3+2a)(−3+2a);1、计算： 抢答：1、判断下列式子是否可用平方差公式。(1)(-2a+b)(-2a-b)(2)(-a+b)(a-b)(3)(a+b)(a-c)(4)（a+b-c)(a+b+c)（是）（否）（否）（是） 学一学例2计算：(1)(y+2)(y−2)−(y-1)(y+5);解:(y+2)(y−2)−(y−1)(y+5)=y2−=22−(y2+4y−5)y2−4−y2−4y+5=−4y+1 练一练计算：(1)(x+2)(x−2)−x(x-1)，其中x=-1.(2008河北中考）解:(x+2)(x−2)−x(x−1)=x2−=22−(x2−x)x2−4−x2+x=x-4当x=-1时，原式=-1-4=-5 2、王敏捷同学去商店买了单价是9.8元/千克的糖果10.2千克，售货员刚拿起计算器，王敏捷就说出应付99.96元.解决实际问题1、计算：102×98解：102×98=（100+2）（100-2）=1002-22=10000-4=9996 拓展练习(1)(2)(2y−x−3z)(−x−2y−3z);计算：(x-3)(x2+9)(x+3) a2−b2;平方差公式应用平方差公式的步骤:思考&总结☞(a+b)(a−b)=步骤：1、判断；2、调整；3、分步解。（注意：要用好括号；幂的运算。）特征（1）两个二项式相乘时，有一项相同，另一项符号相反，积等于相同项的平方减去相反项的平方。（2）公式中的a和b可以是数、字母，也可以是单项式或多项式。 1、三导练习：15.2乘法公式（1）2、课本156页习题15.2第1题布置&作业☞ 再见 达标检测(1)下列多项式的乘法中可以用平方差公式计算的是（）A(x+1)(1+x)B(2a+b)(b-2a)C(-a+b)(a-b)(2)下列各式计算正确的是（）A(a+b)(a-b)=a2+b2B(2x-3y)(2x+3y)=4x2-9C(5ab-1)(5ab+1)=25a2b2-1D(3x+2)(3x-2)=3x2-4(3)若m×(x+3)(x2+9)=x4-81,则m应是（）Ax-3B3-xC3+xDx-9BCA a2-b2=(a+b)(a-b)逆向思维训练：1、（）（）=n2-m22、()()=4x2-9y23、（5+a）()=25-a²