八年级上数学课件《勾股定理》 (10)_苏科版

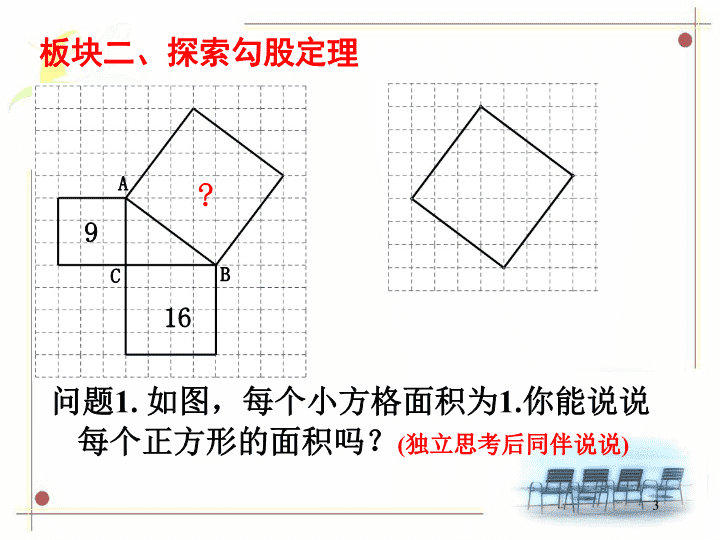
八年级上数学课件《勾股定理》 (10)_苏科版

3.1勾股定理（1）1 1955年希腊发行了一枚纪念邮票，邮票上的图案是根据一个著名的数学定理设计的。问题：观察每个正方形内小方格的个数，请你说说三个正方形的面积有何关系？（独立思考后同伴交流）板块一、初步认识邮票上的勾股图2 板块二、探索勾股定理问题1.如图，每个小方格面积为1.你能说说每个正方形的面积吗？(独立思考后同伴说说)ABC916?3 问题2.怎样计算大正方形的面积？(先独立思考,再同伴互帮)“割”的方法“补”的方法4 问题3.请你说说三个正方形的面积有何关系？(独立思考)问题4.能否用直角三角形的三边表示上述关系？(独立思考后同伴交流)ABC916255 问题5.按下列要求实验并思考：（1）在方格纸上，每组同学任意画同一个顶点都在格点上的Rt△ABC，使∠C=90°；（2）分别以这个直角三角形各边为一边向三角形外作正方形；（3）计算3个正方形的面积；（4）三个正方形的面积有何关系？（5）能否用直角三角形的三边表示上述关系？（小组讨论后先独立操作，再同伴互帮互纠）6 问题6.通过以上探索，请你说说直角三角形三边有怎样的等量关系？(独立思考后同伴说说)勾股定理：直角三角形两条直角边的平方和等于斜边的平方。如图，在△ABC中，∠C=90°，则有。a2+b2=c27 板块三、简单应用勾股定理，并感受其文化问题1.如图，在△ABC中，∠C=90°，若a=5，b=12，则c等于多少？（独立思考）问题2.如图，在△ABC中，∠C=90°，若a=8，c=17，则b等于多少？（独立思考）问题3.如图，在△ABC中，∠C=90°，若两边长分别为3和4，则第三边的平方等于.（独立思考后同伴交流）8 勾股史话两千多年前，古希腊有个毕达哥拉斯学派，他们首先发现了勾股定理，因此在国际上通常称勾股定理为毕达哥拉斯定理。为了纪念这个学派，1955年希腊曾经发行了一枚纪念邮票。我国是最早了解勾股定理的国家之一。早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾（较短直角边）等于三，股（较长直角边）等于四，那么弦（斜边）就等于五，即“勾三股四弦五”，这个结论被记载于我国古代数学著作《周髀算经》中。9 板块四、探究非直角三角形的三边关系问题1.假如∠C变成锐角，如图①，以△ABC三边分别向外作正方形，则面积关系还成立吗？(独立思考后同伴交流)问题2.假如变成钝角呢(如图②)？10 板块五、课堂小结问题1.如图，在Rt△ABC中，∠B=90°，请你说说三边a，b，c的等量关系。(独立思考后同伴说说)问题2.如图，所有四边形都是正方形，所有三角形都是直角三角形，图中数据为该正方形的面积，则最大正方形的边长是。（独立思考后同伴交流）11