八年级上数学课件- 11-3-2 多边形及其内角和 课件（共15张PPT）_人教新课标

八年级上数学课件- 11-3-2 多边形及其内角和 课件（共15张PPT）_人教新课标

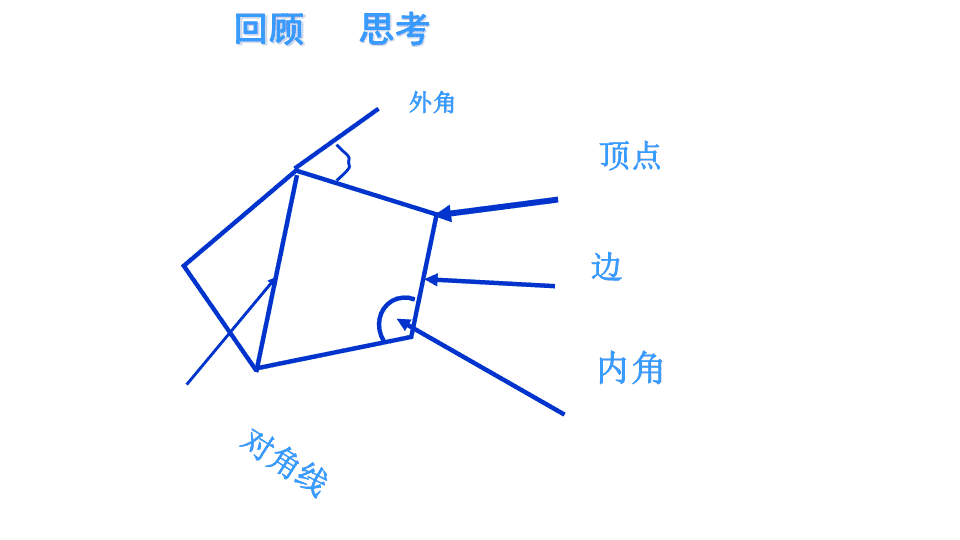
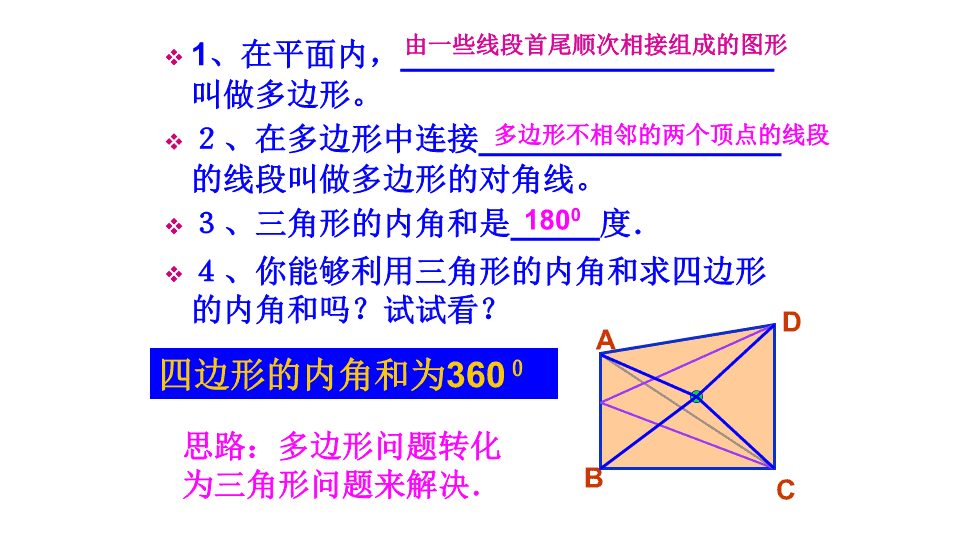
多边形的内角和八年级上人教版数学 顶点边内角对角线回顾思考外角 1、在平面内，_____________________叫做多边形。２、在多边形中连接_________________的线段叫做多边形的对角线。３、三角形的内角和是_____度．４、你能够利用三角形的内角和求四边形的内角和吗？试试看？ABCD思路：多边形问题转化为三角形问题来解决．四边形的内角和为360０由一些线段首尾顺次相接组成的图形多边形不相邻的两个顶点的线段1800 多边形的边数34567…n分成三角形的个数…多边形的内角和…1180°2345360°540°720°900°n－2（n－2）×180°n边形的内角和＝（n－2）·180°探索多（n）边形的内角和 多了什么？如何处理？ABCDABCDEABCDEF这种分割方式，将多边形分成n-1个三角形，故所有三角形的内角和为（n-1）×180°，边上一点周围所形成的平角不是多边形的内角，因此n边形的内角和为（n-1）×180°-180°=(n-2)×180° ABCDABCDEABCDEF该图中n边形共有n个三角形，故所有三角形内角和为n×180°，但每个图中都有一个以红圈圈住的点，它是一个圆周角360°，因此n边形的内角和为n×180°-360°=(n-2)×180°多了什么？如何处理？ 得到定理：n边形的内角和等于(n－2)·180.说明：(1)多边形的内角和仅与边数有关，与多边形的大小、形状无关；(2)强调凸多边形的内角的范围：0<<180.结论: 例1：求八边形的内角和的度数。解：（n－2）×180°＝（8－2）×180°＝1080°答：八边形的内角和为1080°。 例2：一个正多边形的一个内角为150°，你知道它是几边形吗？解：设　这个多边形为n边形，根据题意得：（n－2）×180＝1５0nn＝12答：这个多边形是12边形。另解：由于多边形外角和等于360°而这个正多边形的每个外角都等于180°－150°＝30°，所以这个正多边形的边数等于360°÷30°＝12。 巩固练习：3、多边形内角和为1080°则它是（）边形。4、多边形内角和为1800°则它是（）边形。1、七边形内角和为（）2、十边形内角和为（）5、有一个正多边形的外角是60°，那么该正多边形是正()边形。 探索:分别求出下列多边形的外角和的度数.360°360°360°360°360° 猜想与说理:n边形的外角和是多少度呢?答:都是360°.因为多边形的外角与它相邻的内角是邻补角，所以n边形的外角和加内角和等于n·180°，内角和为(n－2)·180°,因此，外角和为：n·180°－(n－2)·180°=360°.结论:多边形的外角和都等于360°. 例3：一个多边形的内角和等于它的外角和的3倍，它是几边形？解：设它是n边形，则(n-2).180°=3×360°解得：n=8答：它是8边形 例3：一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。解：设一个外角为x°，则内角为（x＋36）°根据题意得：x+x+36＝180x＝72360÷72＝5答：这个正多边形为正五边形。 小结：我们通过把多边形划分为若干个三角形，用三角形内角和去求多边形内角和，从而得到多边形的内角和公式为（ｎ－２）×180°。这种化未知为已知的转化方法，必须在学习中逐渐掌握。由于多边形外角和为360°，与边数无关，所以常把多边形内角和的问题转化为外角和来处理。作业：P90第9、10题