八年级上数学课件- 13-1-1 等腰三角形 课件（ 18张PPT）_人教新课标

八年级上数学课件- 13-1-1 等腰三角形 课件（ 18张PPT）_人教新课标

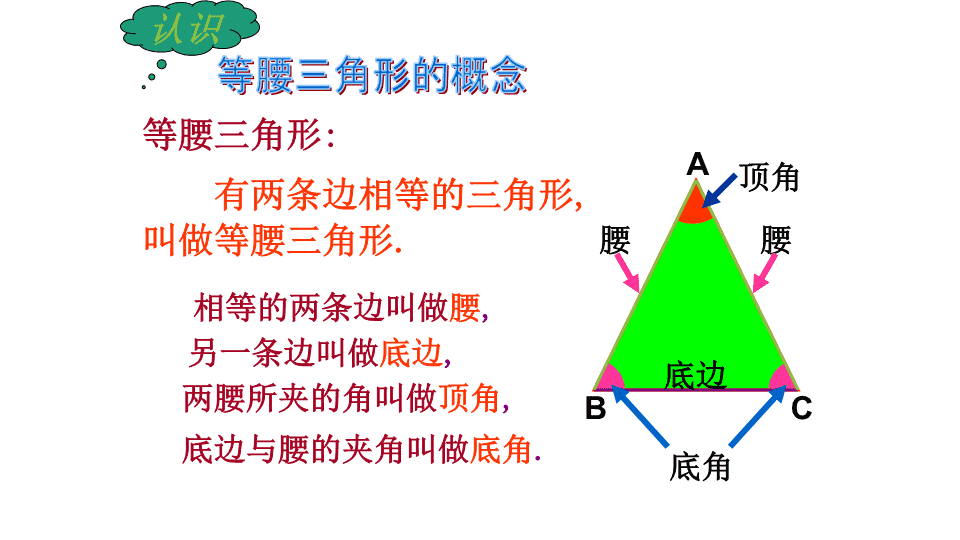
人教版八年级数学上册13.3.1等腰三角形 请同学们欣赏精美的图片:金字塔卢浮宫圣诞树这些图片中有等腰三角形吗？ ABC等腰三角形:有两条边相等的三角形,叫做等腰三角形.等腰三角形的概念相等的两条边叫做腰,另一条边叫做底边,底边与腰的夹角叫做底角.两腰所夹的角叫做顶角,腰腰底边顶角底角认识 如图所示，把一张长方形的纸按图中虚线对折，并剪去阴影部分，再把它展开，得到的△ABC有什么特点？探索并证明等腰三角形的性质ABCD活动（一） 上面剪出的等腰三角形是轴对称图形吗？ABCD把剪出的等腰三角形ABC沿折痕对折，找出其中重合的线段和角，填入下表：重合的线段重合的角等腰三角形除了两腰相等以外,你还能发现它的其他性质吗?AB=ACBD=CDAD=AD∠B=∠C∠ADB=∠ADC∠BAD=∠CAD活动（二）：细心观察大胆猜想 问题1、发现（2）用文字如何表述？等腰三角形的两个底角相等问题2、发现（3）（4）（5）用一句话可以归纳吗？2、∠B=∠C3、BD=CD4、∠ADB=∠ADC=90°5、∠BAD=∠CAD1、等腰三角形是轴对称图形两个底角相等AD为底边上的中线AD为底边上的高AD为顶角平分线我的发现：等腰三角形的底边上的中线、底边上的高和顶角平分线互相重合 CABD如何证明我们的发现？已知：如图△ABC中,AB=AC求证：∠B=∠C证明：过A作AD⊥BC于D∵AD⊥BC，∴∠ADB=∠ADC=90°∟在Rt△ABD和Rt△ACD中AB=AC（已知）AD=AD（公共边）∴Rt△ABD≌Rt△ACD（HL）∴∠B=∠C（全等三角形的对应角相等）等腰三角形的两个底角相等 证明：作底边中线AD.∴BD=CD在△BAD和△CAD中，AB=AC(已知),BD=CD(已证)，AD=AD(公共边),∴△BAD≌△CAD(SSS).∴∠B=∠C(全等三角形的对应角相等).已知：△ABC中，AB=AC.求证：∠B=∠C.ABCD作底边中线思考1：还有其他的证明方法吗？ 已知：△ABC中，AB=AC.求证：∠B=∠C.ABC12证明：作顶角的平分线AD.∴∠1=∠2在△BAD和△CAD中，AB=AC(已知),∠1=∠2(已证)，AD=AD(公共边),∴△BAD≌△CAD(SAS).∴∠B=∠C(全等三角形的对应角相等).作顶角的平分线D CABD如何证明我们的发现？已知：如图△ABC中,AB=AC求证：∠B=∠C证明：过A作AD⊥BC于D∵AD⊥BC，∴∠ADB=∠ADC=90°∟在Rt△ABD和Rt△ACD中AB=AC（已知）AD=AD（公共边）∴Rt△ABD≌Rt△ACD（HL）∴∠B=∠C（全等三角形的对应角相等）等腰三角形的两个底角相等 探究新知：等腰三角形的性质性质1:等腰三角形的两个底角相等（简称“等边对等角”）性质2：等腰三角形的底边上的中线、底边上的高和顶角平分线互相重合（简称“三线合一”）思考：一般的三角形有这种性质吗？要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。 例1.完成例题：已知：在△ABC中，AB＝AC，∠B＝80°．求∠C和∠A的度数。ABC80°根据性质1:等腰三角形的两个底角相等∵∠B=∠C=80°∵∠A=180°-(80°+80°)=20° 例2.如果等腰三角形的一个外角等于140°，那么等腰三角形三个内角等于多少度？如图：∠1+∠2=140°∵∠BAC=180°-140°=40°根据性质1:等腰三角形的两个底角相等∵∠B=∠C=70°∵∠A=40° 例3.在△ABC中，AB＝AC，D是BC边上的中点，∠B＝30°，求∠1和∠ADC的度数。∴AB＝AC，D是BC边上的中点∵△ABC是等腰三角形∵∠B=∠C=30°根据性质2：等腰三角形的底边上的中线、底边上的高和顶角平分线互相重合∵∠ADC=90°∵∠1=60° 小结：1、等腰三角形的性质：1、等边对等角2、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合（三线合一）3、“三线合一”性质在实际应用中，只要推出其中一个结论成立，其它两个结论一下成立，所以关键是寻找其中一个结论成立的条件。本节课你学到了什么? 作业1、已知：如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数。ABCD 作业2：如图所示，已知AB＝AC，AD＝AE，求证：BE＝CD.(要求：用两种不同方法) 谢谢观看