八年级上数学课件- 14-3-2 公式法 课件（共21张PPT）1_人教新课标

八年级上数学课件- 14-3-2 公式法 课件（共21张PPT）1_人教新课标

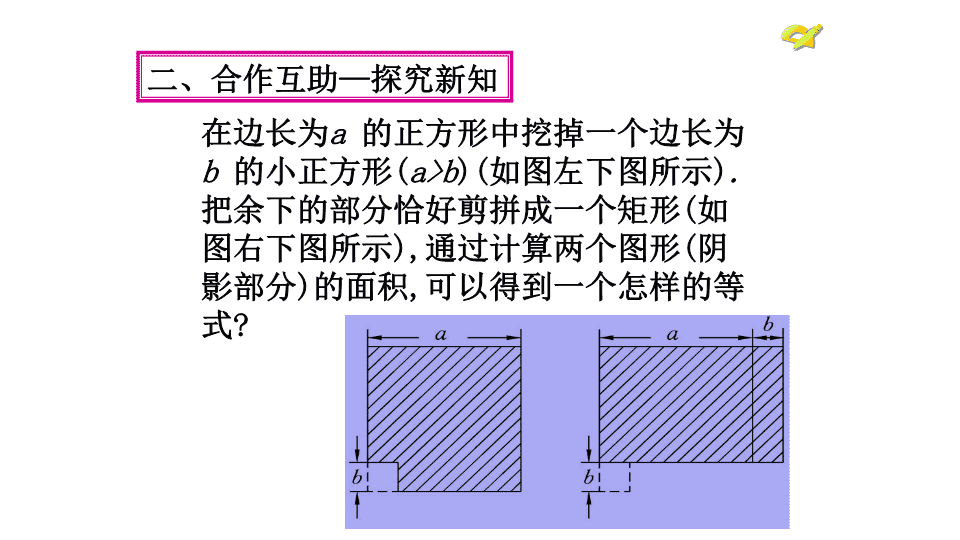
八年级数学·上新课标[人]14.3.2公式法（1）第十四章整式的乘法与因式分解 1、什么叫把多项式分解因式?把一个多项式化成几个整式的积的形式，叫做多项式的分解因式.一、激趣导入—复习旧知2、已学过哪一种分解因式的方法?提公因式法3、【问题】你能将a2-b2分解因式吗?你是如何思考的? 二、合作互助—探究新知在边长为a的正方形中挖掉一个边长为b的小正方形(a>b)(如图左下图所示).把余下的部分恰好剪拼成一个矩形(如图右下图所示),通过计算两个图形(阴影部分)的面积,可以得到一个怎样的等式? 右图中阴影部分为矩形(长为a+b,宽为a-b),面积为(a+b)(a-b).因此(a+b)(a-b)=a2-b2或a2-b2=(a+b)(a-b),(a+b)(a-b)=a2-b2是乘法公式,而反过来a2-b2=(a+b)(a-b)这是因式分解的另一种方法——公式法.通过图形可以知道,右图是由左图拼成的,它们的面积相等,左图中阴影部分的面积为a2-b2; 把乘法公式(a+b)(a-b)=a2-b2反过来就可得到分解因式中的平方差公式:a2-b2=(a+b)(a-b)两个数的平方差,等于这两个数的和与这两个数的差的积.语言叙述 思考此公式有何特点?(1)等号左边：①等号左边应是二项式；②每一项都可以表示成平方的形式；③两项的符号相反．(2)等号右边：是等号左边两底数的和与这两个数的差的积． 练习(1)x2-4=x2-22=(x+2)(x-2);(2)x2-16=(x)2-()2=()();(3)9-y2=()2-()2=()·();(4)1-a2=()2-()2=()·().x4x+4x-43y3+y3-y1a1+a1-a 例1分解因式.(1)4x2-9;(2)(x+p)2-(x+q)2.解析a2-b2=(a+b)(a-b)2xx+p3x+q说明公式中的a与b可以表示一个数,也可以表示一个单项式,甚至是多项式,三、精讲实练：—应用平方差公式 解:(1)4x2-9=(2x)2-32=(2x+3)(2x-3).(2)(x+p)2-(x+q)2=[(x+p)+(x+q)][(x+p)-(x+q)]=(2x+p+q)(p-q). 例2分解因式:(1)x4-y4;(2)a3b-ab.解析(1)x4-y4可以写成(x2)2-(y2)2的形式,这样就可以利用平方差公式进行因式分解了.但分解到(x2+y2)(x2-y2)后,必须进行到多项式的每一个因式都不能再分解为止.(2)不能直接利用平方差公式分解因式,但通过观察可以发现a3b-ab有公因式ab,应先提出公因式,再进一步分解. 1.公式:a2-b2=(a+b)(a-b).2.法则:两个数的平方差,等于这两个数的和与这两个数的差的积.知识小结 3.注意:(1)左边是二项式,每项都是平方的形式,两项的符号相反;(2)右边是两个多项式的积,一个因式是两数的和,另一个因式是这两数的差;(3)在乘法公式中,“平方差”是计算结果,而在因式分解中,“平方差”是要分解因式的多项式;(4)平方差公式的使用条件:如果多项式是两数差的形式,并且这两个数又都可以写成平方的形式,那么这个多项式可以运用平方差公式分解因式. 分解因式：(1)9a2－4b2；(2)x2y－4y；(3)(a＋1)2－1；(4)x4－1；(5)(x＋y＋z)2－(x－y＋z)2.对于(1)可先化成平方差形式，再直接利用平方差公式分解因式；对于(2)可先提取公因式，再利用平方差公式分解因式；对于(3)将(a＋1)视为一个整体运用平方差公式分解因式；对于(5)分别将(x＋y＋z)与(x－y＋z)视为整体，运用平方差公式进行分解因式．导引：四、实练：—应用平方差公式 分解因式：(1)9a2－4b2；(2)x2y－4y；(3)(a＋1)2－1；(4)x4－1；(5)(x＋y＋z)2－(x－y＋z)2.对于(1)可先化成平方差形式，再直接利用平方差公式分解因式；对于(2)可先提取公因式，再利用平方差公式分解因式；对于(3)将(a＋1)视为一个整体运用平方差公式分解因式；对于(5)分别将(x＋y＋z)与(x－y＋z)视为整体，运用平方差公式进行分解因式．导引：四、实练：—应用平方差公式 B解析:a2-9=(a+3)(a-3).故选B.检测反馈1.将a2-9分解因式的结果是()A.(a+9)(a-9)B.(a+3)(a-3)C.(a+3)2D.(a-3)2五、达标检测 B2.将(a-1)2-1分解因式,结果正确的是()A.a(a-1)B.a(a-2)C.(a-2)(a-1)D.(a-2)(a+1)解析:原式=(a-1+1)(a-1-1)=a(a-2).故选B. 3.计算552-152的结果是()A.40B.1600C.2400D.2800D解析:552-152=(55+15)×(55-15)=70×40=2800.故选D. 4.用平方差公式分解因式.(1)36-x2;(2)-a2+b2;(3)x2-16y2;(4)x2y2-z2;(5)(x+2)2-92;(6)(x+a)2-(y+b)2;(7)25(a+b)2-4(a-b)2;(8)a2-16. 解析:直接利用平方差公式进行因式分解.(4)原式=(xy+z)(xy-z).解:(1)原式=(6+x)(6-x).(2)原式=(b+a)(b-a).(3)原式=(x+4y)(x-4y). 课堂总结（1）本节课学习了哪些主要内容？（2）因式分解的平方差公式在应用时应注意什么？ 小练习册课时作业布置作业