八年级下数学课件矩形的性质和判定_鲁教版

八年级下数学课件矩形的性质和判定_鲁教版

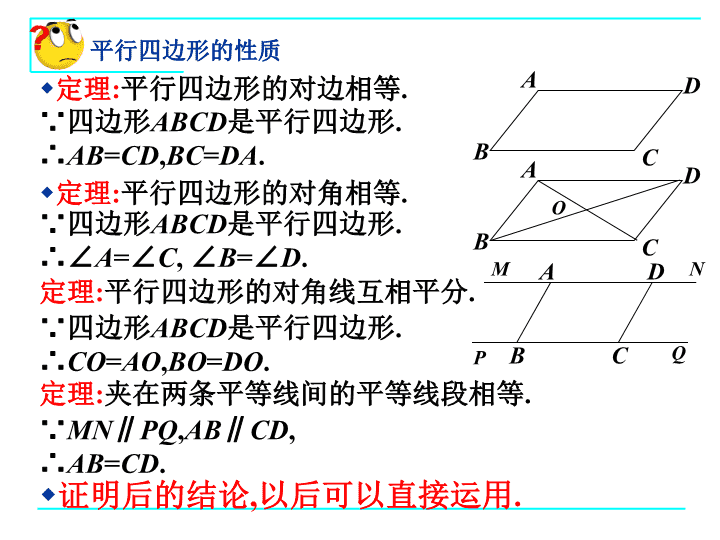
8.2特殊的平行四边形(1)矩形的性质及判定 证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”);(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;(6)检查表达过程是否正确,完善.回顾与思考 定理:平行四边形的对边相等.证明后的结论,以后可以直接运用.BDCA∵四边形ABCD是平行四边形.∴AB=CD,BC=DA.定理:平行四边形的对角相等.∵四边形ABCD是平行四边形.∴∠A=∠C,∠B=∠D.定理:平行四边形的对角线互相平分.∵四边形ABCD是平行四边形.∴CO=AO,BO=DO.BDCAO定理:夹在两条平等线间的平等线段相等.∵MN∥PQ,AB∥CD,∴AB=CD.BDCAMNPQ平行四边形的性质 定理:两组对边分别相等的四边形是平行四边形.定理:一组对边平行且相等的四边形是平行四边形.定理:对角线互相平分的四边形是平行四边形.定理:两组对角分别相等的四边形是平行四边形的.∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.BDCABDCAO∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形.∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.∵∠A=∠C,∠B=∠D.∴四边形ABCD是平行四边形.平行四边形的判定 四边形之间有何关系？特殊的平行四边形之间呢？还记得它们与平行四边形的关系吗?能用一张图来表示它们之间的关系吗?四边形平行四边形矩形菱形正方形两组对边分别平行有一个角是直角有一组邻边相等有一个角是直角有一组邻边相等一组对边平行另一组对边不平行梯形两腰相等等腰梯形腰与底垂直直角梯形四边形之间的关系 定理:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形.分析:由矩形的定义,利用对角相等,邻角互补可使问题得证.证明:∵四边形ABCD是矩形,∴∠A=900,四边形ABCD是平行四边形.∴∠C=∠A=900,∠B=1800-∠A=900,∠D=1800-∠A=900.求证:∠A=∠B=∠C=∠D=900.∴∠A=∠B=∠C=∠D=900DBCA想一想:正方形的四个角都是直角吗?矩形的性质 定理:矩形的两条对角线相等.已知:如图,AC,BD是矩形ABCD的两条对角线.求证:AC=BD.证明:∵四边形ABCD是矩形,∴AB=DC,∠ABC=∠DCB=900.分析:根据矩形的性质性质,可转化为全等三角形(SAS)来证明.DBCA∵BC=CB,∴△ABC≌△DCB(SAS).∴AC=DB.矩形的性质 议一议:设矩形的对角线AC与BD交于点E,那么,BE是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系?为什么?DBCAE由此可得推论:直角三角形斜边上的中线等于斜边的一半.BE是Rt△ABC中斜边AC上的中线.BE等于AC的一半.∵AC=BD,BE=DE,直角三角形的性质 已知:如图,AC,BD是矩形ABCD的两条对角线,AC,BD相交于点O,∠AOD=1200,AB=2.5cm.求矩形对角线的长.解:∵四边形ABCD是矩形,∴BD=2AB=2×2.5=5(cm).∴AC=BD,且∵∠DAB=900,DBCAO∵∠AOD=1200,∴∠ODA=∠OAD=你认为例1还可以怎么去解？例题讲解 定理:有三个角是直角的四边形是矩形.已知:如图,在四边形ABCD中,∠A=∠B=∠C=900.分析:利用同旁内角互补,两直线平行来证明四边形是平行四边形,可使问题得证.证明:∵∠A=∠B=∠C=900,∴∠A+∠B=1800,∠B+∠C=1800.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.DBCA∴四边形ABCD是矩形.矩形的判定 定理:对角线相等的平行四边形是矩形.已知:如图,在□ABCD中,对角线AC=BD.求证:四边形ABCD是矩形.DBCA分析:要证明□ABCD是矩形,只要证明有一个角是直角即可.证明:∴AB=CD,AB∥CD.∵AC=DB,BC=CB,∴△ABC≌△DCB.∴∠ABC=∠DCB.∵四边形ABCD是平行四边形.∵∠ABC+∠DCB=1800.∴∠ABC=900.∴四边形ABCD是矩形.矩形的判定 定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.求证:△ABC是直角三角形已知:CD是△ABC边AB上的中线,且EABCD分析:要证明△ABC是直角三角形,可以点A,B,C构造平行四边形,然后证明其对角线相等,即可证明是矩形.证明:延长CD到E,使DE=DC,连接AE,BE.∴四边形ACBE是平行四边形.∵AB=2CD,CE=2CD,∴CE=AB.∴四边形ACBE是矩形.∵AD=BD,CD=ED,∴∠ACB=900.∴△ABC是直角三角形.直角三角形的判断 定理:矩形的四个角都是直角.定理:矩形的两条对角线相等.推论(直角三角形性质):直角三角形斜边上的中线等于斜边的一半.∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=900.DBCADBCA∵AC,BD是矩形ABCD的两条对角线.∴AC=BD.在△ABC中,∠ACB=900,∵AD=BD,ABCD矩形的判定 定理:有三个角是直角的四边形是矩形.定理:对角线相等的平行四边形是矩形.定理:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.∵∠A=∠B=∠C=900,∴四边形ABCD是矩形.DBCADBCA∵AC,BD是□ABCD的两条对角线,且AC=DB.∴四边形ABCD是矩形.ABCD∴∠ACB=900.在△ABC中,∵AD=BD=CD,矩形的判定 独立作业P84习题8.41,2,3题.