八年级下数学课件八年级下册数学课件《平行四边形的判定的综合练习》 北师大版 (2)_北师大版

八年级下数学课件八年级下册数学课件《平行四边形的判定的综合练习》 北师大版 (2)_北师大版

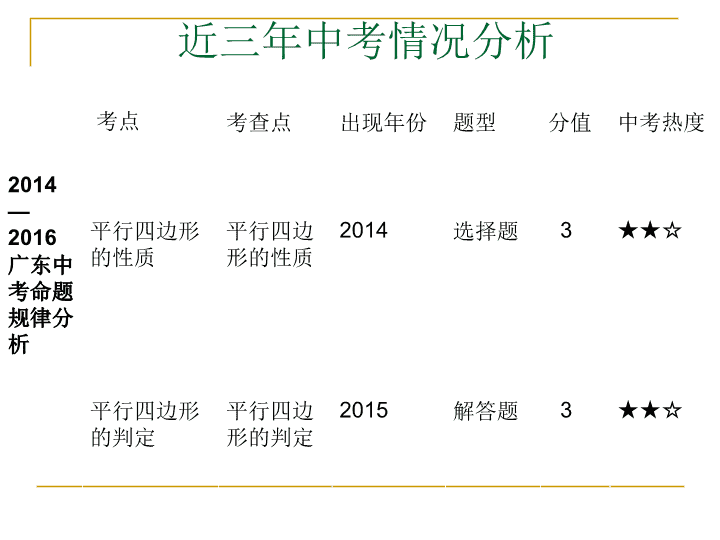
平行四边形（复习课） 考情分析考纲要求1、理解平行四边形的概念了解四边形的不稳定性2、探索并证明平行四边形的有关性质定理：平行四边形的对边相等、对角相等、对角线互相平分探索并证明平行四边形的判定定理：一组对边平行且相等的四边形是平行四边形、两组对边分别相等的四边形是平行四边形、对角线互相平分的四边形是平行四边形3、了解两平行线之间距离的意义，能度量两平行线之间的距离 近三年中考情况分析2014—2016广东中考命题规律分析考点考查点出现年份题型分值中考热度平行四边形的性质平行四边形的性质2014选择题3★★☆平行四边形的判定平行四边形的判定2015解答题3★★☆ 知识梳理1、平行四边形的概念定义:有两组对边分别平行的四边形。（1）平行四边形的定义揭示了图形的最本质的属性，它既是平行四边形的一条性质，又是一个判定方法.（2）表示方法：用符号“□”表示平行四边形，例如：平行四边形ABCD记作“□ABCD”，读作“平行四边形ABCD”. （1）边：平行四边形两组对边分别.（2）角：平行四边形的对角，邻角.（3）对角线：平行四边形的对角线.（4）对称性：平行四边形是对称图形.但不是对称图形（5）周长：平行四边形的周长等于一组邻边和的二倍（6）面积：①计算公式：S□=底×高=ah.②平行四边形的一条对角线将四边形分成两个全等的三角形.平行四边形的两条对角线将四边形分成四个面积相等的三角形相等互补平行且相等互相平分中心轴2.平行四边形的性质 3.平行四边形的判定（1）由定义：两组对边分别平行的四边形是平行四边形.（2）两组对边分别相等的四边形是平行四边形.（3）一组对边平行且相等的四边形是平行四边形.（4）两组对角分别相等的四边形是平行四边形.（5）对角线互相平分的四边形是平行四边形. 考点1平行四边形的性质考点精讲【例1】（2016深圳）如图1-4-6-1，在□ABCD中，AB=3，BC=5，以点B为圆心，以任意长为半径作弧，分别交BA，BC于点P，Q，再分别以P，Q为圆心，以大于PQ的长为半径作弧，两弧在∠ABC内交于点M，连接BM并延长交AD于点E，则DE的长为________.思路分析：根据作图过程可得BE平分∠ABC；再根据角平分线的性质和平行四边形的性质可得∠AEB=∠CBE，证出AE=AB=3，即可得出DE的长.123 解：根据作图的方法，得BE平分∠ABC，∴∠ABE=∠CBE.∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC=5.∴∠AEB=∠CBE.∴∠ABE=∠AEB.∴AE=AB=3.∴DE=AD-AE=5-3=2.答案：2 考题再现1.（2014广东）如图1-4-6-2，□ABCD中，下列说法一定正确的是（　　）A.AC=BDB.AC⊥BDC.AB=CDD.AB=BC2.如图1-4-6-3，在平行四边形ABCD中，∠ABC的平分线交AD于点E，∠BED=150°，则∠A的大小为（　　）A.150°B.130°C.120°D.100°CC123 考点演练3.如图1-4-6-7，□ABCD的对角线AC,BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE.下列结论：①∠CAD=30°；②S□ABCD=AB·AC；③OB=AB；④OE=BC,成立的有（　　）A.1个B.2个C.3个D、4个C 4.如图1-4-6-9，在□ABCD中，O是对角线AC和BD的交点，OE⊥AD于点E，OF⊥BC于点F.求证：OE=OF.证明：∵四边形ABCD是平行四边形，∴OA=OC，AD∥BC.∴∠EAO=∠FCO.∵OE⊥AD，OF⊥BC，∴∠AEO=∠CFO=90°.∴△AEO≌△CFO（AAS）.∴OE=OF 考点点拨：本考点是广东中考的高频考点，题型不固定，难度中等.解答本考点的有关题目，关键在于熟练掌握平行四边形的性质定理：对边平行且相等、对角相等、对角线互相平分。在有关平行四边形性质的题目中，常涉及全等三角形的证明，这样的出题方式，备考时需多加留意. 考点2平行四边形的判定考点精讲【例2】（2014深圳）如图1-4-6-10，已知BD垂直平分AC，∠BCD=∠ADF，AF⊥AC，求证：四边形ABDF是平行四边形.思路点拨：先证得△ADB≌△CDB,求得∠BCD=∠BAD，从而得到∠ADF=∠BAD，所以AB∥FD，因为BD⊥AC，AF⊥AC，所以AF∥BD，即可得证. 证明：∵BD垂直平分AC，∴AB=BC，AD=DC.∵BD=BD∴△ADB≌△CDB（SSS）.∴∠BCD=∠BAD.∵∠BCD=∠ADF∴∠BAD=∠ADF，∴AB∥FD.∵BD⊥AC，AF⊥AC，∴AF∥BD.∴四边形ABDF是平行四边形. 考题再现1.（2015广州）下列命题中，真命题的个数有（　　）①对角线互相平分的四边形是平行四边形;②两组对角分别相等的四边形是平行四边形;③一组对边平行，另一组对边相等的四边形是平行四边形.④如果一个四边形任意相邻的两个内角都互补，那么这个四边形是平行四边形⑤三条边相等的四边形是平行四边形0个B.1个C.2个D.3个E、4个F、5个D 2、如图1-4-6-11，□ABCD中，点E，F在对角线BD上，且BE=DF，求证：（1）AE=CF；（2）四边形AECF是平行四边形.证明：（1）∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD.∴∠ABE=∠CDF.在△ABE和△CDF中，∴△ABE≌△DCF（SAS）.∴AE=CF.（2）∵△ABE≌△DCF，∴∠AEB=∠CFD.∴∠AEF=∠CFE.∴AE∥CF.又∵AE=CF，∴四边形AECF是平行四边形. 3.如图1-4-6-12，已知四边形ABCD，对角线AC和BD相交于点O，下面选项不能得出四边形ABCD是平行四边形的是（　　）A.AB∥CD，AB=CDB.AB=CD，AD=BCC.AO=CO，BO=DOD.AB∥CD，AD=BCD 4.如图1-4-6-13，在△ABC中，∠ABC=90°，∠BAC=60°，△ACD是等边三角形，E是AC的中点，连接BE并延长，交DC于点F，求证：（1）△ABE≌△CFE；（2）四边形ABFD是平行四边形. （2）∵E是AC的中点，∴BE=EA.∵∠BAE=60°，∴△ABE是等边三角形.∴△CEF是等边三角形.∴∠CFE=60°.∵△ACD是等边三角形，∴∠CDA=∠DCA=60°.∴∠CFE=∠CDA.∴BF∥AD.∵∠DCA=∠BAC=60°，∴AB∥DC.∴四边形ABFD是平行四边形. 考点点拨：本考点的题型不固定，难度中等.解答本考点的有关题目，关键在于熟练掌握平行四边形的判定定理，从而对有关平行四边形的结论进行判断或证明.熟记以下五种平行四边形的判定方法：（1）定义法：两组对边分别平行的四边形是平行四边形；（2）方法2：两组对边分别相等的四边形是平行四边形；（3）方法3：一组对边平行且相等的四边形是平行四边形.（4）方法4：两组对角分别相等的四边形是平行四边形；（5）方法5：对角线互相平分的四边形是平行四边形； 1.（2016泸州）如图1-4-6-19，□ABCD的对角线AC，BD相交于点O，且AC+BD=16，CD=6，则△ABO的周长是（　　）A.10B.14C.20D.22B课堂巩固训练 2.如图1-4-6-20，在四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是（　　）A.AB∥CD，AD∥BCB.OA=OC，OB=ODC.AD=BC，AB∥CDD.AB=CD，AD=BCC 3.如图1-4-6-21，四边形ABCD中，AB=CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE.若DE=BF，则下列结论：①CF=AE；②OE=OF；③四边形ABCD是平行四边形；④图中共有四对全等三角形.其中正确结论的个数是（　　）A.4个B.3个C.2个D.1个B 4.（2016张家界）如图1-4-6-23，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F.试判断四边形ABFC的形状，并证明你的结论.解：四边形ABFC是平行四边形.证明：∵AB∥CD，∴∠BAE=∠CFE.∵E是BC的中点，∴BE=CE.在△ABE和△FCE中，∴△ABE≌△FCE（AAS）.∴AE=EF.又∵BE=CE,∴四边形ABFC是平行四边形. 同学们：望你们乘上数学之舟，科学之箭，闯荡未来的人生。再见！下课了!