2019七年级数学下册 第五章 相交线与平行线 5相交线

2019七年级数学下册 第五章 相交线与平行线 5相交线

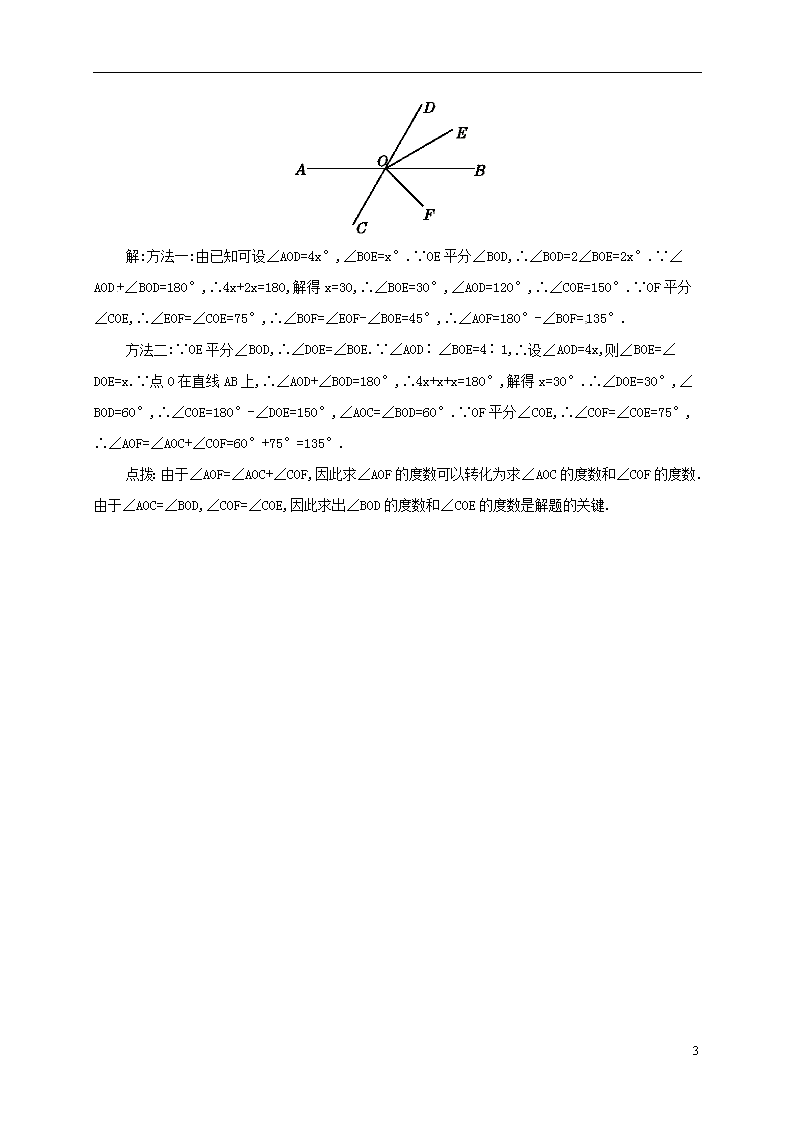
第五章 ‎5.1.1‎相交线 知识点1:相交线 当两条直线有且只有一个公共点时,则称这两条直线相交,如图.‎ 知识点2：邻补角 ‎1. 定义:两条直线相交所得的四个角中,有一条公共边,另一边互为反向延长线的两个角是邻补角.如图,∠1和∠2有一条公共边OA,它们的另一边互为反向延长线,具有这种关系的两个角,称互为邻补角.‎ ‎2. 性质:如果∠1和∠2是一对邻补角,那么∠1+∠2=180°.‎ 注意：(1)判定两个角是否为邻补角,关键是看这两个角的两边是否满足“其中一边是公共边,另一边互为反向延长线”的条件.‎ ‎(2)邻补角是成对的,包含了两层含义:①是位置关系:相邻;②是数量关系:两角之和等于180°.‎ ‎(3)邻补角也可以看作是一条直线与端点在这条直线上的一条射线组成的两个角.‎ ‎(4)注意邻补角和补角的区别:邻补角一定互补,但互补的两个角不一定是邻补角.因为邻补角既相邻又互补,但互补的两个角不管其位置如何,只要它们的和为180°就是一对互补的角. 知识点3：对顶角 ‎1. 定义:两个角,如果它们有一个公共的顶点,并且角的两边互为反向延长线,那么它们就互为对顶角.如图,∠1和∠3,∠2和∠4互为对顶角.‎ 3‎ ‎2. 性质:对顶角相等.‎ 注意:(1)判断两角是否为对顶角,要抓住它的特征:①有公共顶点;②两个角的两边互为反向延长线.‎ ‎(2)对顶角是成对出现的,单独一个角不能构成对顶角.‎ ‎(3)互为对顶角的两个角相等,但相等的两个角不一定是对顶角. ‎ 考点1:利用对顶角、邻补角建立起角度之间的联系 ‎【例1】　如图,直线AB,CD,EF相交于点O,∠AOE=30°,∠BOC=2∠AOC,求∠DOF的度数.‎ 解:设∠AOC=x°,则∠BOC=2x°.‎ ‎ 由邻补角的定义得2x+x=180.‎ 解之,得x=60.∴∠AOC=60°.‎ ‎∴∠EOC=∠AOC-∠AOE=60°-30°=30°.‎ ‎∴∠DOF=∠EOC=30°.‎ 点拨：∠EOC与∠DOF互为对顶角,因此要求∠DOF的度数只需求出∠EOC的度数.由已知∠BOC=2∠AOC且∠BOC与∠AOC互为邻补角,从而可求出∠BOC和∠AOC的度数,再由∠EOC的度数等于∠AOC和∠AOE的度数之差,且∠AOE的度数已知,不难求出∠EOC的度数.‎ 考点2:角度计算问题常见解题思路 ‎【例2】　如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE,∠AOD∶∠BOE=4∶1,求∠AOF的度数.‎ 3‎ 解:方法一:由已知可设∠AOD=4x°,∠BOE=x°.∵OE平分∠BOD,∴∠BOD=2∠BOE=2x°.∵∠AOD+∠BOD=180°,∴4x+2x=180,解得x=30,∴∠BOE=30°,∠AOD=120°,∴∠COE=150°.∵OF平分∠COE,∴∠EOF=∠COE=75°,∴∠BOF=∠EOF-∠BOE=45°,∴∠AOF=180°-∠BOF=135°.‎ 方法二:∵OE平分∠BOD,∴∠DOE=∠BOE.∵∠AOD∶∠BOE=4∶1,∴设∠AOD=4x,则∠BOE=∠DOE=x.∵点O在直线AB上,∴∠AOD+∠BOD=180°,∴4x+x+x=180°,解得x=30°.∴∠DOE=30°,∠BOD=60°,∴∠COE=180°-∠DOE=150°,∠AOC=∠BOD=60°.∵OF平分∠COE,∴∠COF=∠COE=75°,∴∠AOF=∠AOC+∠COF=60°+75°=135°.‎ 点拨：由于∠AOF=∠AOC+∠COF,因此求∠AOF的度数可以转化为求∠AOC的度数和∠COF的度数.由于∠AOC=∠BOD,∠COF=∠COE,因此求出∠BOD的度数和∠COE的度数是解题的关键.‎ 3‎