三角形的三边关系教案2

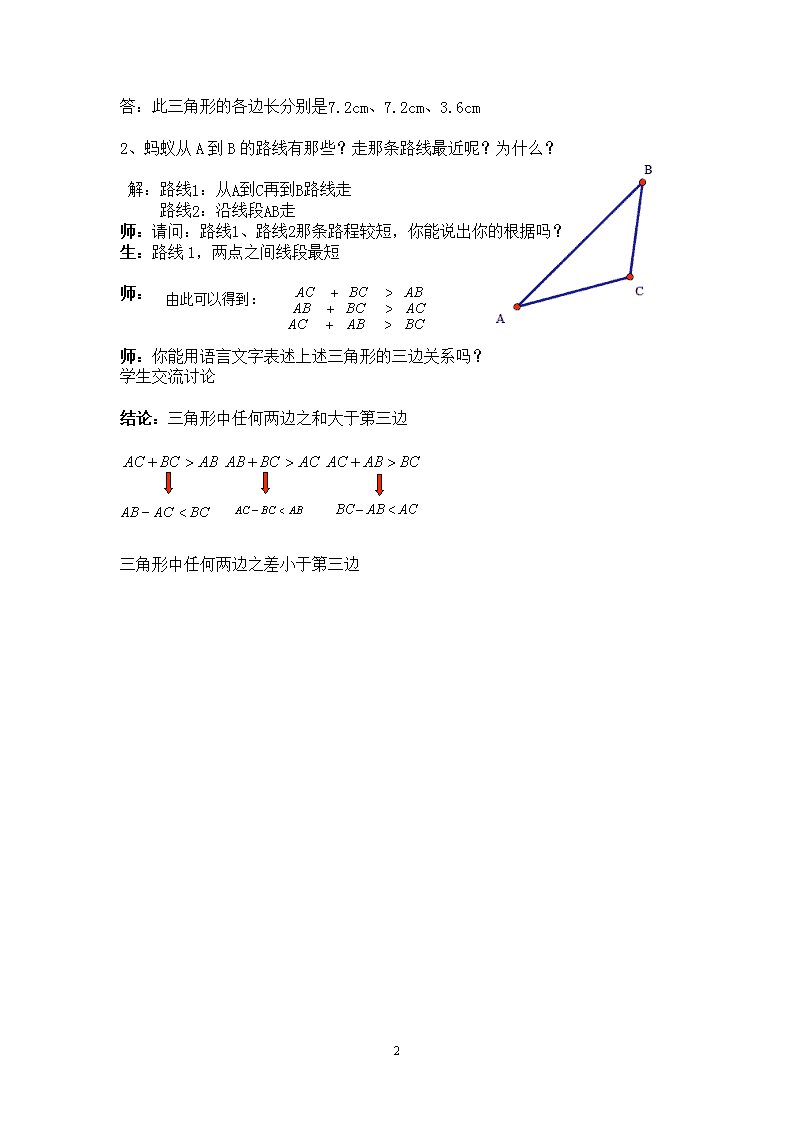
三角形的三边关系教案2

‎ ‎ ‎9.1.3 三角形的三边关系 ‎ 教学目标 : ‎ ‎ 1.知识与技能目标：‎ ‎ 让学生通过作三角形(已知三条线段)的过程中，发现“三角形任何两边之和大于第三边”．并会利用这个不等量关系判断不知的三条线段能否组成三角形以及已知三角形的二边会求第三边的取值范围.会利用三角形的稳定性解决一些实际问题.‎ ‎2．过程与方法目标：‎ ‎ 通过观察、操作、想像、推理和交流活动，发展学生的空间观念、推理能力和有条理、清晰地表达自己观点的能力。‎ ‎ 3情感、态度、价值观目标：‎ ‎ 体现三角形与生活的紧密联系，鼓励学生努力学好文化知识，为社会做贡献。‎ ‎ 通过对问题的发现和解决，使学生有成就感，培养学生的合作精神，树立学好数学的信心。‎ 教学重点、难点 ‎ ‎ ‎ ‎1.重点:三角形任何两边之和大于第三边的应用. ‎ ‎2难点：已知三角形的两边求第三边的范围．‎ 教师活动 复习提问：‎ 1、 三角形的定义：由三条不在同一条直线上的线段首尾顺次连结组成的平面图形，称为三角形.‎ ‎ 2、三角形还有那些性质：三角形的三个内角和是多少?三角形的外角有什么性质?‎ ‎ 三角形的内角和为180度，外角和为360度 4‎ ‎ ‎ 学生活动 ‎1、已知：等腰三角形的周长是18cm，腰是底边长的2倍，求各边长.‎ 解：底边长为xcm，则腰为2xcm ‎ 2x+2x+x=18‎ ‎ 解得：x=3.6‎ ‎ 则腰为7.2‎ 4‎ ‎ ‎ 答：此三角形的各边长分别是7.2cm、7.2cm、3.6cm ‎2、蚂蚁从A到B的路线有那些？走那条路线最近呢？为什么？‎ ‎ 解：路线1：从A到C再到B路线走 ‎ 路线2：沿线段AB走 4‎ ‎ ‎ 师：请问：路线1、路线2那条路程较短，你能说出你的根据吗？‎ 生：路线1，两点之间线段最短 ‎ ‎ 由此可以得到：‎ 师：‎ 师：你能用语言文字表述上述三角形的三边关系吗？‎ 学生交流讨论 结论：三角形中任何两边之和大于第三边 ‎ ‎ 三角形中任何两边之差小于第三边 4‎ ‎ ‎ 三角形的稳定性：‎ 学生活动：‎ ‎ 做一个三角形，使它的三边分别为4cm、3cm、2.5.然后同桌之间相互比较所作的三角形是否一样？（一模一样）‎ ‎ ‎ 师： 如果三角形的三边固定，那么三角形的形状和大小能被固定下来吗？‎ ‎ 结论：如果三角形的三边固定，那么三角形的形状和大小就完全确定了，三角形的这个性质叫做三角形的稳定性 学生活动：‎ ‎1、练一练：‎ 下列长度的各组线段能否组成一个三角形？‎ ‎（1）15cm、10cm、7cm (2) 4cm、5cm、10cm ‎ (3) 3cm、8cm、5cm (4) 4cm、5cm、6cm ‎ 只要满足较小的两条线段之和大于第三条线段，便可构成三角形;若不满足，则不能构成三角形.‎ 师：思考：有两条长度分别为5cm和7cm的线段，要组成一个三角形那么第三条线段的长度在什么范围内呢？ ‎ ‎ ‎ 解题技巧： 三角形第三边的取值范围是: ‎ ‎ 两边之差<第三边<两边之和 ‎1、已知：等腰三角形周长为18cm，如果一边长等于4cm，求另两边的长？‎ 解：若底边长为4cm，设腰长为xcm，则有 ‎ 2x+4=18‎ ‎ x=7‎ ‎2、若一条腰长为4cm，设底边长为xcm，则有 ‎ 2×4+x=18‎ ‎ x=10‎ 因为4+4<10，所以，以4cm为腰不能构成三角形.‎ 所以，三角形另来那个边长都是7cm 练一练 ‎1、五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.‎ ‎2、如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长=______________.‎ ‎3、如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长=______________.‎ 4‎ ‎ ‎ 课堂小结：‎ 1、 三角形的三边关系定理 ‎2、三角形的任何两边的和大于第三边 ‎ (1)判断三条已知线段能否组成三角形时，采用一种较为简便的判法：‎ 若最短边与较长边的和大于最长边，则可构成三角形，否则不能.‎ ‎ (2)确定三角形第三边的取值范围：‎ ‎ 两边之差<第三边＜两边之和．‎ 3、 三角形的稳定性 4‎