2017-2018学年湖南省常德市澧县七年级数学下册期末复习试卷（一）含答案

2017-2018学年湖南省常德市澧县七年级数学下册期末复习试卷（一）含答案

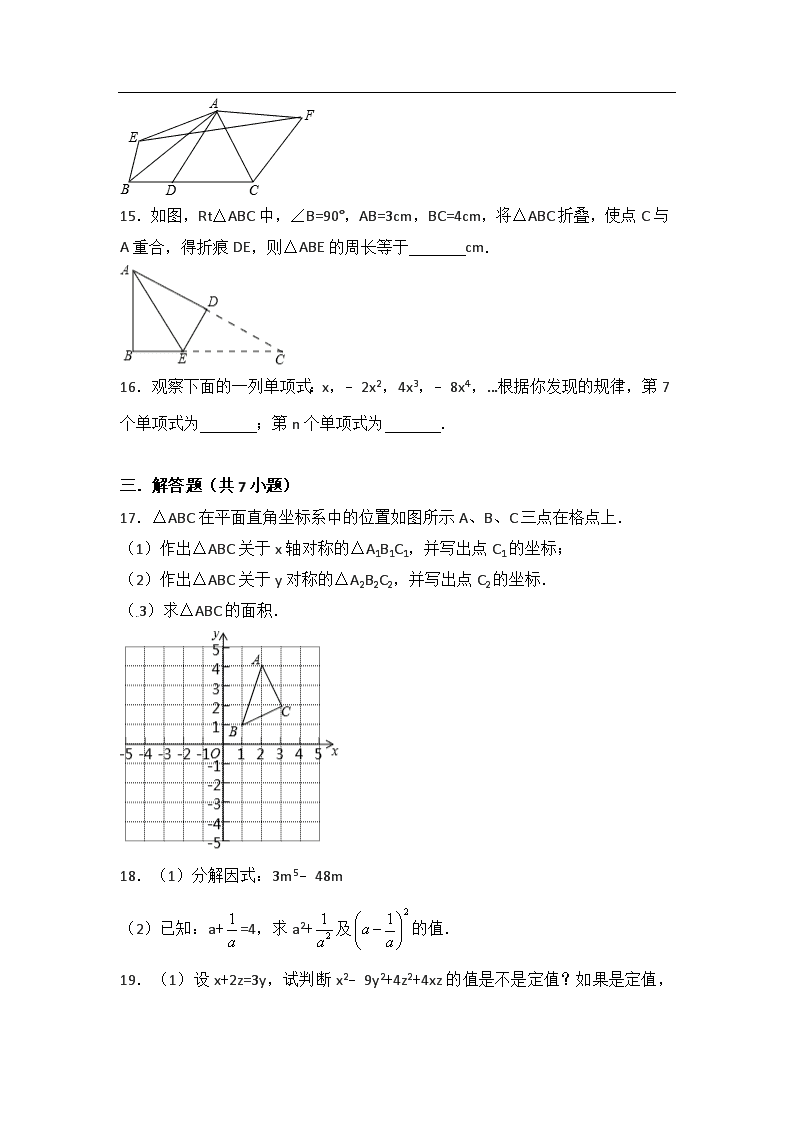
湖南省澧县2017—2018学年湘教版版七年级数学下册期末复习试卷（一）与简答 一．选择题（共8小题）‎ ‎1．下面四个手机应用图标中是轴对称图形的是（　　）‎ A． B． C． D．‎ ‎2．如果，则x：y的值为（　　）‎ A． B． C．2 D．3‎ ‎3．下列式子正确的是（　　）‎ A．a2﹣4b2=（a+2b）（a﹣2b） B．（a﹣b）2=a2﹣b2‎ C．（a+b）2=a2+b2 D．（x+3y）（x﹣3y）=x2﹣3y2‎ ‎4．已知一个圆的半径为Rcm，若这个圆的半径增加2cm，则它的面积增加（　　）‎ A．4cm2 B．（2R+4）cm2 C．（4R+4）cm2 D．以上都不对 ‎5．已知如图，直线a⊥c，b⊥c，∠1=140°，那么∠2的度数是（　　）‎ A．40° B．50° C．60° D．140°‎ ‎6．若等式x2+ax+19=（x﹣5）2﹣b成立，则 a+b的值为（　　）‎ A．16 B．﹣16 C．4 D．﹣4‎ ‎7．玩具车间每天能生产甲种玩具零件24个或乙种玩具零件12个，若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具，怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天，乙种玩具零件y天，则有（　　）‎ A． B．‎ C． D．‎ ‎8．某青年排球队12名队员的年龄情况如表：‎ 年龄 ‎18[来源:学#科#网Z#X#X#K]‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ 人数 ‎1‎ ‎4‎ ‎3‎ ‎2‎ ‎2‎ 则这个队队员年龄的众数和中位数是（　　）‎ A．19，20 B．19，19 C．19，20.5 D．20，19‎ ‎　‎ 二．填空题（共8小题）‎ ‎9．若（a+b+5）2+|2a﹣b+1|=0，则（b﹣a）2017=　 　．‎ ‎10．若am=2，an=3，则a3m+2n=　 　．‎ ‎11．一台机床生产一种零件，5天内出现次品的件数为：1，0，1，2，1．则出现次品的方差为　 　．‎ ‎12．如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．若∠1=35°，则∠2的度数为　 　．‎ ‎[来源:Zxxk.Com]‎ ‎13．如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为　 　．‎ ‎14．如图，△ABC中，∠BAC=75°，BC=7，△ABC的面积为14，D为 BC边上一动点（不与B，C重合），将△ABD和△ACD分别沿直线AB，AC翻折得到△ABE与△ACF，那么△AEF的面积最小值为　 　．‎ ‎15．如图，Rt△ABC中，∠B=90°，AB=3cm，BC=4cm，将△ABC折叠，使点C与A重合，得折痕DE，则△ABE的周长等于　 　cm．‎ ‎16．观察下面的一列单项式：x，﹣2x2，4x3，﹣8x4，…根据你发现的规律，第7个单项式为　 　；第n个单项式为　 　．‎ ‎　‎ 三．解答题（共7小题）‎ ‎17．△ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上．‎ ‎（1）作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；‎ ‎（2）作出△ABC关于y对称的△A2B2C2，并写出点C2的坐标．‎ ‎（3）求△ABC的面积．‎ ‎18．（1）分解因式：3m5﹣48m ‎（2）已知：a+=4，求a2+及的值．[来源:学科网]‎ ‎19．（1）设x+2z=3y，试判断x2﹣9y2+4z2+‎ ‎4xz的值是不是定值？如果是定值，求出它的值；否则请说明理由．‎ ‎（2）已知x2﹣2x=2，将下式先化简，再求值：（x﹣1）2+（x+3）（x﹣3）+（x﹣3）（x﹣1）．‎ ‎20．甲、乙两人同解方程组，甲正确解得，乙因抄错C解得，求A、B、C的值．‎ ‎21．已知，直线AB∥CD，E为AB、CD间的一点，连接EA、EC．‎ ‎（1）如图①，若∠A=20°，∠C=40°，则∠AEC=　 　°．‎ ‎（2）如图②，若∠A=x°，∠C=y°，则∠AEC=　 　°．‎ ‎（3）如图③，若∠A=α，∠C=β，则α，β与∠AEC之间有何等量关系．并简要说明．‎ ‎22．如图所示，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并对结论进行说理．‎ ‎23．2015年体育中考在即，学校体育组对九（1）班50名学生进行了长跑项目的测试，根据测试成绩制作了如图两个统计图．‎ 根据统计图解答下列问题：‎ ‎（1）本次测试的学生中，得4分的学生有多少人？‎ ‎（2）本次测试的平均分是多少？‎ ‎（3）通过一段时间的训练，体育组对该班学生的长跑项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中，得4分、5分的学生分别有多少人？‎ ‎　‎ 湖南省澧县张公庙中学2017—2018学年湘教版版七年级数学下册期末复习试卷（一）简答 一．选择题（共8小题）‎ ‎1． A． 2． D． 3． A． 4． D． 5． A． 6． D． 7． C． 8．A．‎ 二．填空题（共8小题）‎ ‎9．　﹣1　． 10．　72　． 11．　0.4　． 12．　55°　．‎ ‎13．　36°或37°　． 14．　4　． 15．　7　cm．‎ ‎16．　64x7　； 　（﹣2）n﹣1xn　．‎ 三．解答题（共7小题）[来源:学科网ZXXK]‎ ‎17．△ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上．‎ ‎（1）作出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；‎ ‎（2）作出△ABC关于y对称的△A2B2C2，并写出点C2的坐标．‎ ‎（3）求△ABC的面积．‎ ‎【分析】（1）分别作出△ABC三顶点关于x轴的对称点，再顺次连接即可得；‎ ‎（2）分别作出△ABC三顶点关于y轴的对称点，再顺次连接即可得；‎ ‎（3）割补法求解可得．‎ ‎【解答】解：（1）如图，△A1B1C1即为所求；‎ 点C1的坐标（3，﹣2）‎ ‎（2）如图，△A2B2C2即为所求；点C2的坐标 （﹣3，2）．‎ ‎（3）S△ABC=2×3﹣×1×2﹣×1×2﹣×1×3=2.5．‎ ‎【点评】本题主要考查作图﹣轴对称变换，解题的关键是根据轴对称变换的定义和性质得出△ABC三顶点的对应点．‎ ‎　‎ ‎18．（1）分解因式：3m5﹣48m ‎（2）已知：a+=4，求a2+及的值．‎ ‎【分析】（1）原式提取公因式，再利用平方差公式分解即可；‎ ‎（2）原式利用完全平方公式化简后，将已知等式代入计算即可求出值．‎ ‎【解答】解：（1）原式=3m（m4﹣16）=3m（m2+4）（m+2）（m﹣2）；‎ ‎（2）∵a+=4，‎ ‎∴原式=（a+）2﹣2=16﹣2=14；‎ 原式=a2+﹣2=14﹣2=12．‎ ‎【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．‎ ‎　[来源:学科网ZXXK]‎ ‎19．（1）设x+2z=3y，试判断x2﹣9y2+4z2+4xz的值是不是定值？如果是定值，求出它的值；否则请说明理由．‎ ‎（2）已知x2﹣2x=2，将下式先化简，再求值：（x﹣1）2+（x+3）（x﹣3）+（x﹣3）（x﹣1）．‎ ‎【分析】（1）可把已知条件化为x﹣3y=﹣2z，把代数式中的x2﹣9y2因式分解，再把x﹣3y=﹣2z代入化简可知代数式的值是否是定值；‎ ‎（2）把原式化简为含x2﹣2x的代数式，再整体代入计算．‎ ‎【解答】解：（1）定值为0，理由如下：‎ ‎∵x+2z=3y，∴x﹣3y=﹣2z，‎ ‎∴原式=（x﹣3y）（x+3y）+4z2+4xz，‎ ‎=﹣2z（x+3y）+4z2+4xz，‎ ‎=﹣2xz﹣6yz+4z2+4xz，‎ ‎=4z2+2xz﹣6yz，‎ ‎=4z2+2z（x﹣3y），‎ ‎=4z2﹣4z2，‎ ‎=0．‎ ‎（2）原式=x2﹣2x+1+x2﹣9+x2﹣4x+3，‎ ‎=3x2﹣6x﹣5，‎ ‎=3（x2﹣2x）﹣5，‎ 当x2﹣2x=2时，原式=3×2﹣5=1．‎ ‎【点评】考查的是整式的混合运算，主要考查了公式法、多项式与多项式相乘以及合并同类项的知识点，还要注意整体思想的应用．‎ ‎　‎ ‎20．甲、乙两人同解方程组，甲正确解得，乙因抄错C解得，求A、B、C的值．‎ ‎【分析】根据方程组的解的定义得到关于A、B、C的方程组，再进一步运用加减消元法求解．‎ ‎【解答】解：把代入原方程组，得 ‎，‎ 把代入Ax+By=2，得 ‎2A﹣6B=2．‎ 可组成方程组，‎ 解得．‎ ‎【点评】此题较简单，只要明白二元一次方程组的解的定义以及方程组的解法就可．‎ ‎　‎ ‎21．已知，直线AB∥CD，E为AB、CD间的一点，连接EA、EC．‎ ‎（1）如图①，若∠A=20°，∠C=40°，则∠AEC=　60　°．‎ ‎（2）如图②，若∠A=x°，∠C=y°，则∠AEC=　360﹣x﹣y　°．‎ ‎（3）如图③，若∠A=α，∠C=β，则α，β与∠AEC之间有何等量关系．并简要说明．‎ ‎【分析】首先都需要过点E作EF∥AB，由AB∥CD，可得AB∥CD∥EF．‎ ‎（1）根据两直线平行，内错角相等，即可求得∠AEC的度数；‎ ‎（2）根据两直线平行，同旁内角互补，即可求得∠AEC的度数；‎ ‎（3）根据两直线平行，内错角相等；两直线平行，同旁内角互补，即可求得∠AEC的度数．‎ ‎【解答】解：如图，过点E作EF∥AB，‎ ‎∵AB∥CD，‎ ‎∴AB∥CD∥EF．‎ ‎（1）∵∠A=20°，∠C=40°，‎ ‎∴∠1=∠A=20°，∠2=∠C=40°，‎ ‎∴∠AEC=∠1+∠2=60°；‎ ‎（2）∴∠1+∠A=180°，∠2+∠C=180°，‎ ‎∵∠A=x°，∠C=y°，‎ ‎∴∠1+∠2+x°+y°=360°，‎ ‎∴∠AEC=360°﹣x°﹣y°；‎ ‎（3）∠A=α，∠C=β，‎ ‎∴∠1+∠A=180°，∠2=∠C=β，‎ ‎∴∠1=180°﹣∠A=180°﹣α，‎ ‎∴∠AEC=∠1+∠2=180°﹣α+β．‎ ‎【点评】此题考查了平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补．解此题的关键是准确作出辅助线：作平行线，这是此类题目的常见解法．‎ ‎　‎ ‎22．如图所示，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠‎ C的大小关系，并对结论进行说理．‎ ‎【分析】由图中题意可先猜测∠AED=∠C，那么需证明DE∥BC．题中说∠1+∠2=180°，而∠1+∠4=180°所以∠2=∠4，那么可得到BD∥EF，题中有∠3=∠B，所以应根据平行得到∠3与∠ADE之间的关系为相等．就得到了∠B与∠ADE之间的关系为相等，那么DE∥BC．‎ ‎【解答】证明：∵∠1+∠4=180°（邻补角定义）‎ ‎∠1+∠2=180°（已知）‎ ‎∴∠2=∠4（同角的补角相等）‎ ‎∴EF∥AB（内错角相等，两直线平行）‎ ‎∴∠3=∠ADE（两直线平行，内错角相等）‎ 又∵∠B=∠3（已知），‎ ‎∴∠ADE=∠B（等量代换），‎ ‎∴DE∥BC（同位角相等，两直线平行）‎ ‎∴∠AED=∠C（两直线平行，同位角相等）．‎ ‎【点评】本题是先从结论出发得到需证明的条件，又从所给条件入手，得到需证明的条件．属于典型的从两头往中间证明．‎ ‎　‎ ‎23．2015年体育中考在即，学校体育组对九（1）班50名学生进行了长跑项目的测试，根据测试成绩制作了如图两个统计图．‎ 根据统计图解答下列问题：‎ ‎（1）本次测试的学生中，得4分的学生有多少人？‎ ‎（2）本次测试的平均分是多少？‎ ‎（3）通过一段时间的训练，体育组对该班学生的长跑项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中，得4分、5分的学生分别有多少人？‎ ‎【分析】（1）用总人数乘以得4分的人数所占的百分比即可；‎ ‎（2）根据平均数的计算公式先求出测试的总分数，再除以总人数即可；‎ ‎（3）设第二次测试中得4分的学生有x人，得5分的学生有y人，根据得4分和5分的人数共有45人和平均分比第一次提高了0.8分，列出方程，求出x，y的值即可．‎ ‎【解答】解：（1）得4分的学生有50×50%=25（人）；‎ ‎（2）本次测试的平均分是： =3.7（分）；‎ ‎（3）设第二次测试中得4分的学生有x人，得5分的学生有y人，‎ 由题意，得，‎ 解得：．‎ 答：第二次测试中得4分的学生有15人，得5分的学生有30．‎ ‎【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ ‎　‎