七年级下册数学教案5-3-1 第2课时 平行线的性质和判定及其综合运用 人教版

七年级下册数学教案5-3-1 第2课时 平行线的性质和判定及其综合运用 人教版

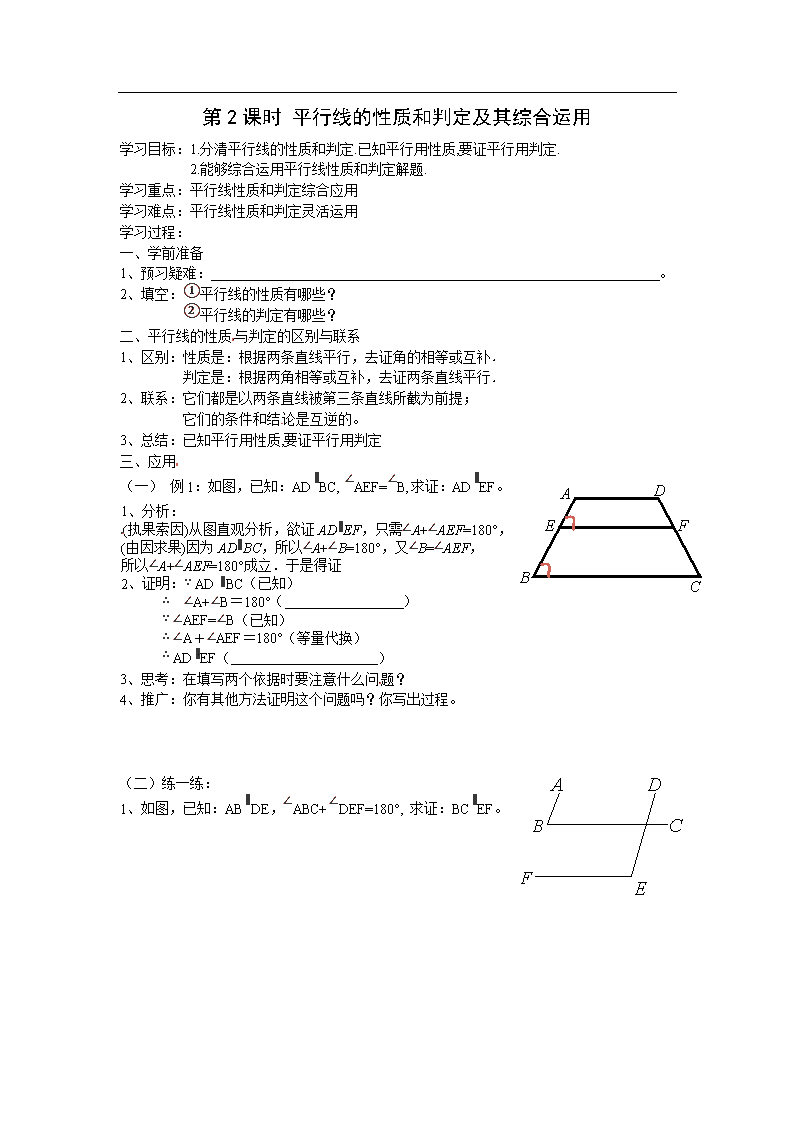
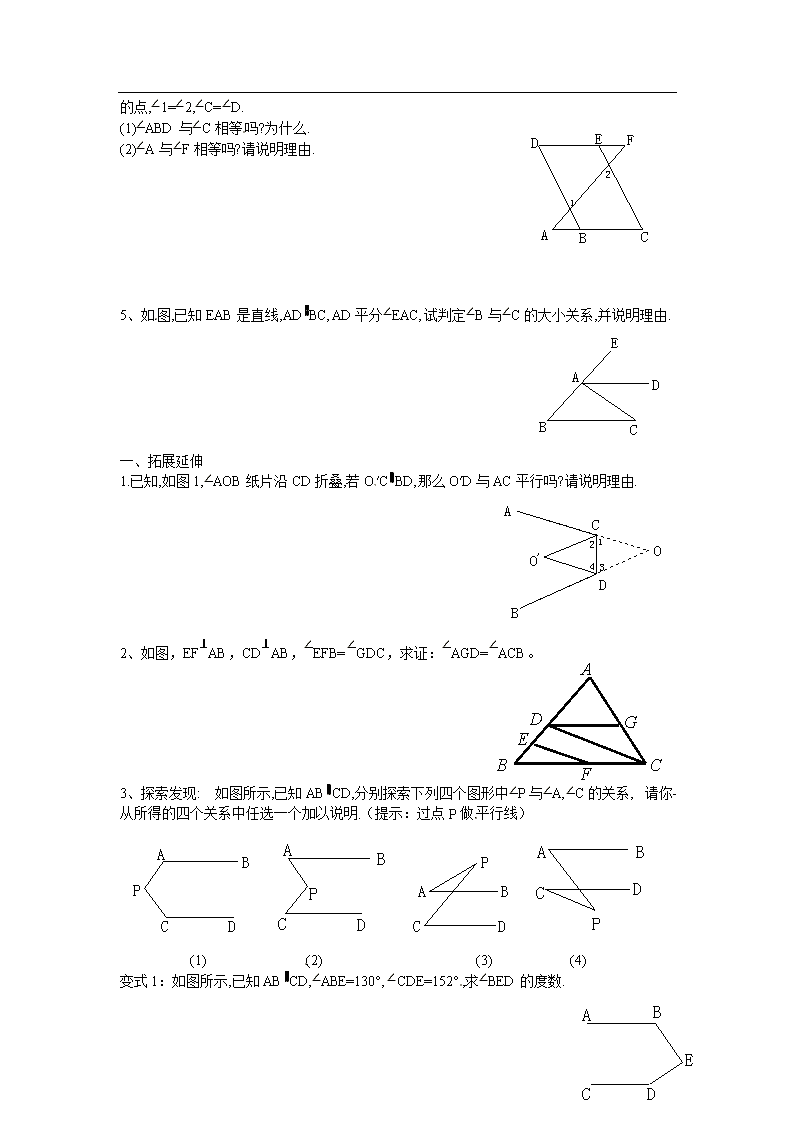
第2课时 平行线的性质和判定及其综合运用 学习目标：1.分清平行线的性质和判定.已知平行用性质,要证平行用判定.‎ ‎2.能够综合运用平行线性质和判定解题.‎ 学习重点：平行线性质和判定综合应用 学习难点：平行线性质和判定灵活运用 学习过程：‎ 一、学前准备 ‎1、预习疑难： 。‎ ‎2、填空：①平行线的性质有哪些？‎ ‎②平行线的判定有哪些？‎ 二、平行线的性质与判定的区别与联系 ‎1、区别：性质是：根据两条直线平行，去证角的相等或互补．‎ 判定是：根据两角相等或互补，去证两条直线平行．[来源:学科网ZXXK]‎ ‎2、联系：它们都是以两条直线被第三条直线所截为前提；‎ 它们的条件和结论是互逆的。‎ ‎3、总结：已知平行用性质,要证平行用判定 三、应用 ‎（一） 例1：如图，已知：AD∥BC, ∠AEF=∠B,求证：AD∥EF。‎ ‎1、分析：‎ ‎(执果索因)从图直观分析，欲证AD∥EF，只需∠A+∠AEF=180°，‎ ‎(由因求果)因为AD∥BC，所以∠A+∠B=180°，又∠B=∠AEF，‎ 所以∠A+∠AEF=180°成立．于是得证 ‎2、证明：∵ AD ∥BC（已知）‎ ‎ ∴ ∠A+∠B＝180°（ ）‎ ‎ ∵ ∠AEF=∠B（已知）‎ ‎ ∴ ∠A＋∠AEF＝180°（等量代换）‎ ‎ ∴ AD∥EF（ ）‎ ‎3、思考：在填写两个依据时要注意什么问题？‎ ‎4、推广：你有其他方法证明这个问题吗？你写出过程。[来源:学。科。网]‎ ‎（二）练一练：‎ ‎1、如图，已知：AB∥DE，∠ABC+∠DEF=180°, 求证：BC∥EF。 ‎ ‎2、如图，已知：∠1＝∠2，求证：∠3＋∠4=180o ‎ ‎3、如图，已知：AB ∥CD，MG平分∠AMN ,NH平分∠DNM，求证：MG∥NH。‎ ‎ ‎ ‎4、如图，已知：AB∥CD，∠A＝∠C， 求证：AD∥BC。‎ ‎[来源:学科网ZXXK]‎ ‎ ‎ 四、学习体会：‎ ‎1、本节课你有哪些收获？你还有哪些疑惑？2、预习时的疑难解决了吗？‎ 五、自我检测：‎ ‎1、如图1,AB∥EF,∠ECD=∠E,则CD∥AB.说理如下:‎ ‎ 因为∠ECD=∠E,[来源:学§科§网Z§X§X§K]‎ ‎ 所以CD∥EF( )‎ ‎ 又AB∥EF,[来源:学+科+网]‎ ‎ 所以CD∥AB( ). （1）‎ ‎2、下列说法:①两条直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④垂直于同一直线的两直线平行,其中是平行线的性质的是( )‎ ‎ A.① B.②和③ C.④ D.①和④‎ ‎3、如图,平行光线AB、DE照射在平面镜上，经反射得到光线BC与EF，已知∠1= ∠2，‎ ‎ ∠3= ∠4，则光线BC与EF平行吗？为什么？‎ A B C D E F ‎1‎ ‎3‎ ‎2‎ ‎4‎ ‎4、如图,已知B、E分别是AC、DF上的点,∠1=∠2,∠C=∠D. ‎ ‎(1)∠ABD与∠C相等吗?为什么.‎ ‎(2)∠A与∠F相等吗?请说明理由.‎ ‎5、如图,已知EAB是直线,AD∥BC,AD平分∠EAC,试判定∠B与∠C的大小关系,并说明理由.‎ 一、 拓展延伸 ‎1.已知,如图1,∠AOB纸片沿CD折叠,若O′C∥BD,那么O′D与AC平行吗?请说明理由.‎ ‎2、如图，EF⊥AB，CD⊥AB，∠EFB=∠GDC，求证：∠AGD=∠ACB。‎ ‎3、探索发现: 如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以说明.（提示：过点P做平行线）‎ ‎ (1) (2) (3) (4)‎ 变式1：如图所示,已知AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED的度数.‎ 变式2：如图所示,AB∥CD,则∠A+∠E+∠F+∠C等于( )‎ A.180° B.360° C.540° D.720°‎