- 2021-10-26 发布 |
- 37.5 KB |
- 6页
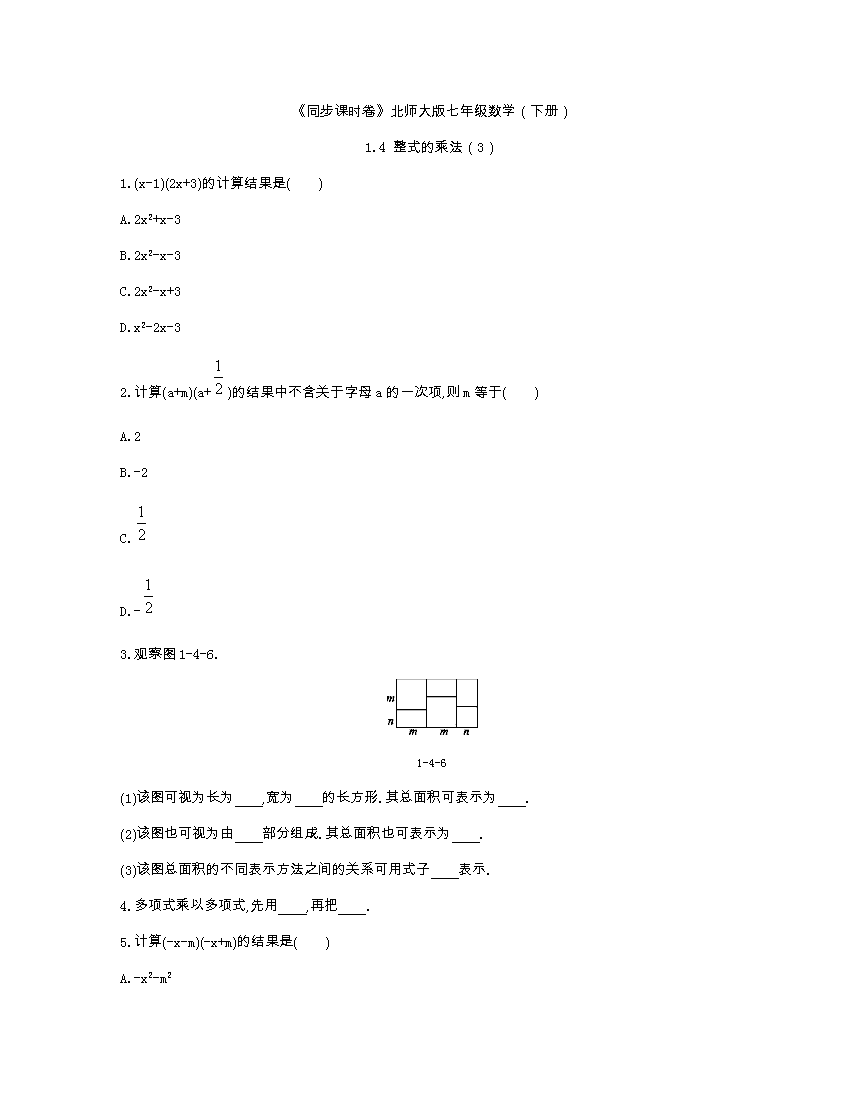


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
《同步课时卷》北师大版七年级数学(下册)1
《同步课时卷》北师大版七年级数学(下册) 1.4 整式的乘法(3) 1.(x-1)(2x+3)的计算结果是( ) A.2x2+x-3 B.2x2-x-3 C.2x2-x+3 D.x2-2x-3 2.计算(a+m)(a+)的结果中不含关于字母a的一次项,则m等于( ) A.2 B.-2 C. D.- 3.观察图1-4-6. 1-4-6 (1)该图可视为长为 ,宽为 的长方形.其总面积可表示为 . (2)该图也可视为由 部分组成.其总面积也可表示为 . (3)该图总面积的不同表示方法之间的关系可用式子 表示. 4.多项式乘以多项式,先用 ,再把 . 5.计算(-x-m)(-x+m)的结果是( ) A.-x2-m2 B.-x2+m2 C.x2-m2 D.x2+m2 6.下列各式中,结果错误的是( ) A.(x+2)(x-3)=x2-x-6 B.(x+4)(x-4)=x2-16 C.(2x+3)(2x-6)=2x2-3x-18 D.(2x-1)(2x+2)=4x2+2x-2 7.若(x+2)(x-5)=x2+px+q,则( ) A.p=-3,q=10 B.p=-3,q=-10 C.p=7,q=-10 D.p=7,q=10 8.计算(x2-4x+n)(x2+mx+8)的结果不含x2和x3的项,那么m= ,n= . 9.已知三角形的底边是(6a+2b)cm,对应底上的高是(2b-6a)cm,则这个三角形的面积是 cm2. 10.计算: (1)(2x+4)(6x-); (2)(a2+3)(a-2)-a(a2-2a-2). 11.先化简,再求值. (x-y)·(x-2y)-(2x-3y)(x+2y),其中x=-2,y=. 12.若(x2+px+q)(x2-2x-3)展开后不含x2和x3项,求p、q的值. 13.设多项式A是三项式,B是四项式,则A×B的结果的多项式的项数一定( ) A.多于7项 B.不多于7项 C.多于12项 D.不多于12项 14.下列算式中,正确的有( ) ①(x+y)2=x2+y2; ②(x-2y)(x+2y)=x2+4xy-4y2; ③(x-3)(x2+3x+9)=x3-27; ④(a-2b2)(m-n)=am-an-2b2m+2b2n. A.1个 B.2个 C.3个 D.4个 15.若在(2x+1)(x2-mx+3)中不含x2项,则m的值是( ) A. B.1 C.- D.-1 16.若a2+a+1=2,则(5-a)(6+a)= . 17.设x*y定义为x*y=(x+1)(y+1),x*2定义为x*2=x*x,则当x=2时,多项式3*(x*2)-2*x+1的值为 . 18.计算: (1)(3x-2y)(y-3x)-(2x-y)(3x+y); (2)(3x+2y+4)(5x-2y-1). 19.(1)计算(x+1)(x+2)= , (x-1)(x-2)= , (x-1)(x+2)= , (x+1)(x-2)= . (2)你发现(1)小题有何特征,用公式表示出来. (3)已知a、b、m均为整数,且(x+a)(x+b)=x2+mx+12,则m的可能取值有多少个? 参考答案 1.A 2.D 3.(1)(2m+n)(m+n)(2m+n)(m+n) (2)六m2+mn+m2+mn+mn+n2 (3)(2m+n)(m+n)=2m2+3mn+n2 4.一个多项式的每一项去乘另一个多项式的每一项所得的积相加 5.C 6.C 7.B 8.4 8 9.(2b2-18a2) 10.(1)12x2+21x-6 (2)5a-6 11.解:原式化简得-xy+5y2, 原式的值为. 12.解:因为(x2+px+q)(x2-2x-3) =x4-2x3-3x2+px3-2px2-3px+qx2-2qx-3q =x4+(p-2)x3-(2p-q+3)x2-(3p+2q)x-3q, 而题意要求展开后不含x2和x3项, 所以p-2=0,2p-q+3=0, 解得p=2,q=7. 13.D 14.B 15.A 16.29 17.32 18.(1)10xy-15x2-y2 (2)15x2+4xy-4y2+17x-10y-4 19.(1)解:(x+1)(x+2)=x2+3x+2, (x-1)(x-2)=x2-3x+2, (x-1)(x+2)=x2+x-2, (x+1)(x-2)=x2-x-2. (2)可以发现第(1)问中,左右两边式子符合(x+p)(x+q)=x2+(p+q)x+pq结构. (3)因为12可以分解成以下6组数,a×b=1×12=2×6=3×4=(-1)×(-12)=(-2)×(-6)=(-3)×(-4),所以m=a+b可有6个值.查看更多